Riyaziyyat

Riyaziyyat (yun. μάθημα, máthēma, "bilik, elm, öyrənmək") — ədədlər (hesab və ədədlər nəzəriyyəsi), düsturlar və əlaqəli strukturlar (cəbr), fiqurlar və fəzalar (həndəsə), kəmiyyətlər və onların dəyişmələri (riyazi analiz) kimi mövzuların öyrənilməsini əhatə edir. Onun dəqiq əhatə dairəsi və ya epistemoloji statusu haqqında ortaq razılaşma yoxdur.

E.ə. III əsr yunan riyaziyyatçısı Evklid (əlində pərgarla). Rafaelin Afina məktəbi freskasından fraqment (1509–1511)

Riyazi fəaliyyətin əsas hissəsi abstrakt (mücərrəd) obyektlərin xassələrini aşkarlamaqdan və isbat etməkdən (saf mühakimə yolu ilə) ibarətdir. Bu obyektlər ya təbiətdən təcridetmə yoluyla (məsələn, natural ədədlər və ya xətlər), ya da (müasir riyaziyyatda) aksiomlar adlanan əsas xassələrlə müəyyən edilən abstrakt varlıqlardır. İsbat bəzi deduktiv qaydaların artıq məlum olan nəticələrə, o cümlədən qabaqcadan isbatlanmış teoremlərə, aksiomlara və (təbiətdən təcridetmə halında) nəzərdən keçirilən nəzəriyyənin həqiqi başlanğıc nöqtələri hesab edilən bəzi əsas xassələrə ardıcıl tətbiqindən ibarətdir. İsbatın nəticəsi teorem adlanır.

Bir sıra elmlərdə hadisələrin modelləşdirilməsi üçün riyaziyyatdan geniş istifadə olunur. Bu, eksperimental qanunlardan kəmiyyət nəticələrini çıxarmağa imkan yaradır. Məsələn, Nyutonun cazibə qanununun köməyilə planetlərin hərəkətini yüksək dəqiqliklə təxmin etmək olar. Riyazi həqiqətin hər hansı təcrübədən müstəqil olması belə proqnozların doğruluğunun yalnız reallığı təsvir edən modelin adekvatlığından asılı olduğunu nəzərdə tutur. Beləliklə, bəzi qeyri-dəqiq proqnozlar ortaya çıxdıqda, bu, riyaziyyatın yanlışlığından deyil, modelin təkmilləşdirilməli və ya dəyişdirilməli olduğundan xəbər verir. Məsələn, Merkurinin periheli Nyutonun cazibə qanunu ilə izah etmək olmaz, lakin bu Eynşteynin ümumi nisbilik nəzəriyyəsi ilə dəqiq izah olunur. Eynşteynin bu nəzəriyyəsinin eksperimental təsdiqi onu göstərir ki, Nyutonun cazibə qanunu yalnız bir növ yaxınlaşmadır (lakin gündəlik həyatda hələ də çox dəqiqdir).

Riyaziyyat təbiət elmləri, mühəndislik, tibb, maliyyə, kompüter elmi və sosial elmlər də daxil olmaqla bir çox sahə üçün vacibdir. Riyaziyyatın bəzi sahələri, məsələn, statistika və oyunlar nəzəriyyəsi, onların tətbiqi ilə birbaşa əlaqəli şəkildə inkişaf etdirilir və çox vaxt tətbiqi riyaziyyat adı altında qruplaşdırılır. Digər riyazi sahələr hər hansı bir tətbiqdən asılı olmayaraq inkişaf etdirilir (və buna görə də saf riyaziyyat adlanır), lakin bir çox hallarda onların da praktik tətbiqləri sonralar aşkar edilir. Uyğun bir nümunə, tarixi Evklidə qədər gedib çıxan, amma RSA kriptosistemində (kompüter şəbəkələrinin təhlükəsizliyi üçün) istifadə edilməmişdən öncə praktik tətbiqə malik olmayan tamı vuruqlara ayırma problemidir.

Riyaziyyat yazılı qeydlərin mövcud olduğu antik dövrlərdən bəri bəşəri fəaliyyət sahəsi olmuşdur. Bununla belə, "isbat" anlayışı və onunla əlaqəli "riyazi ciddilik" ilk dəfə Yunan riyaziyyatında, xüsusilə də Evklidin Başlanğıclar əsərində ortaya çıxır. Riyaziyyat, cəbr və sonsuz kiçiklər hesabının əsas riyazi sahələr kimi hesab və həndəsəyə qoşulduğu İntibah dövrünə qədər nisbətən zəif sürətlə inkişaf etdi. O vaxtdan bəri riyazi yeniliklər və elmi kəşflər arasındakı qarşılıqlı əlaqə riyazi kəşflərin xeyli dərəcədə artmasına səbəb oldu. 19-cu əsrin sonunda riyaziyyatın əsaslı böhranı aksiomatik metodun sistemləşdirilməsinə səbəb oldu. Bu isə öz növbəsində riyaziyyatın və onun tətbiq sahələrinin sayca kəskin artmasına səbəb oldu; riyaziyyatın altmışdan çox birinci səviyyəli sahəsini qeyd edən bölmələr üzrə təsnifat bunu təsdiqləyir.

Riyaziyyatın sahələri

Abak qədim zamanlardan istifadə edilən sadə hesablama alətidir.

İntibahdan əvvəl riyaziyyat iki əsas sahəyə: ədədlər üzərindəki əməllərə həsr olunmuş hesaba və fiqurları öyrənən həndəsəyə ayrılırdı. Bu dövrdə riyaziyyatdan xeyli faydalanan numerologiya və astrologiya kimi psevdoelmlər də mövcud idi.

İntibah dövründə iki əsas sahə meydana çıxdı. Riyazi işarələrin tətbiqi, kobud desək, düsturların öyrənilməsi və onlar üzərindəki əməllərdən ibarət olan cəbrə gətirib çıxardı. Diferensial və inteqral hesabı, qısaca "kalkyulus" arqumentlərin dəyişməsini və onlar arasındakı əlaqəni modelləşdirən kəsilməz funksiyaların tədqiqidir. Dörd əsas sahəyə görə aparılan bu bölgü 19-cu əsrin sonlarına qədər qüvvədə qaldı, baxmayaraq ki, çox vaxt riyaziyyata aid edilən göy mexanikası və kimi bəzi sahələr indi fizikaya aid edilir. Həmçinin, bu dövrdə inkişafda olan bəzi fənlər, ancaq sonralar muxtar sahələr olaraq qəbul edilən ehtimal nəzəriyyəsi və kombinatorika kimi riyaziyyatın (müxtəlif hissələrə bölünmüş) sahələrindən öncə mövcud idi.

19-cu əsrin sonlarında riyaziyyatın böhranı və bunun nəticəsində də aksiomatik metodun sistemləşdirilməsi riyaziyyat sahələrində həcmi partlayışa səbəb oldu.

20-ci əsrin əvvəllərində riyaziyyatda mövcud olan istiqamətlər haqqında tarixi Paris Konqresinin bölmələrinin siyahısına əsasən fikir söyləmək olar. Bu, əsas dörd bölmədən: hesab və cəbr; analiz; həndəsə; mexanika və riyazi fizika, həmçinin daha iki: tarix və biblioqrafiya; tədris və metodologiya bölmələrindən ibarətdir.

O dövrdən keçən zaman ərzində elmdə olan dəyişikliklər barədə müasir konqreslərin bölmələr siyahısına əsasən məlumat əldə etmək olar: riyazi məntiq və riyaziyyatın əsasları; cəbr; ədədlər nəzəriyyəsi; həndəsə; topologiya; cəbri həndəsə; kompleks analiz; Li qrupu və göstərişlər nəzəriyyəsi; həqiqi və funksional analiz; ehtimal nəzəriyyəsi və riyazi statistika; xüsusi törəməli diferensial tənliklər; adi diferensial tənliklər; riyazi fizika; ədədi üsullar və hesablama nəzəriyyəsi; diskret riyaziyyat və kombinatorika; informatikanın riyazi aspektləri; qeyri-fiziki fənlərə riyaziyyatın tətbiqi; riyaziyyat tarixi; riyaziyyatın tədrisi.

Ədədlər nəzəriyyəsi

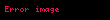
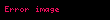
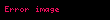
Ədədlər nəzəriyyəsinin inkişafı ədədlər, yəni natural (${\displaystyle \mathbb {N} }$), tam (${\displaystyle \mathbb {Z} }$) və rasional (${\displaystyle \mathbb {Q} }$) ədədlər üzərindəki əməllərlə başladı. Qədimdə ədədlər nəzəriyyəsi hesab adlanırdı, lakin indi bu termin daha çox ədədlərlə bağlı hesablama üsulları üçün istifadə olunur.

Ədədlər nəzəriyyəsinin özünəməxsusluğu ondan ibarətdir ki, o elementar kimi görünən bir çox çətin məsələləri həll etmək üçün təkmil həll metodlarından istifadə edir. Diqqətəlayiq bir nümunə, 1637-ci ildə Pyer Ferma tərəfindən ifadə edilmiş və yalnız 1994-cü ildə Endryu Uils tərəfindən kateqoriya nəzəriyyəsi və homoloji cəbrin köməyilə isbat edilən Fermanın son teoremidir. Başqa bir misal, 2-dən böyük hər bir cüt tam ədədin iki sadə ədədin cəmi olduğunu iddia edən Qoldbax fərziyyəsidir. 1742-ci ildə Xristian Qoldbax tərəfindən bildirilmişdir ki, bu, xeyli səylərə baxmayaraq isbatsız qalır.

Tədqiq olunan problemlərin və həll üsullarının müxtəlifliyi baxımından ədədlər nəzəriyyəsi hazırda bir neçə alt sahəyə bölünür, bunlara analitik ədədlər nəzəriyyəsi, cəbri ədədlər nəzəriyyəsi, ədədlərin həndəsəsi (metod yönümlü), Diofant tənlikləri və transendent nəzəriyyə (problem yönümlü) daxildir.

Həndəsə

Həndəsə hesab ilə birlikdə riyaziyyatın ən qədim qollarından biridir. O, əsasən ölçmə və memarlığın ehtiyaclarından ortaya çıxan xətlər, bucaqlar və çevrələr kimi formalara aid empirik təriflərlə başlandı.

Əsas yenilik qədim yunanlar tərəfindən isbatların işlənib hazırlanması idi: məsələn, iki uzunluğun bərabər olduğunu ölçmə ilə yoxlamaq kifayət deyil. Belə bir xassə əvvəllər isbat edilmiş nəticələrdən (teoremlərdən) və əsas xassələrdən (bunlar isbatın (postulatların) predmeti olmaq üçün çox sadə olduğuna görə özlüyündə aydın hesab olunur) mücərrəd əsaslandırma ilə isbat edilməlidir. Bütün riyaziyyatın əsasını təşkil edən bu prinsip həndəsə üçün işlənib hazırlanmış və təqribən miladdan öncə 300-cü ildə Evklid tərəfindən Başlanğıclar kitabında sistemləşdirilmişdir.

Nəticədə meydana çıxan Evklid həndəsəsi Evklid müstəvisində (müstəvi həndəsəsində) və (üçölçülü) Evklid fəzasında xətlər, müstəvilər və çevrələrin köməyilə qurulan fiqurların öyrənilməsidir.

Evklid həndəsəsi 17-ci əsrə qədər, Rene Dekartın indi Kartezian koordinatları adlanan şeyi təqdim etməsinə qədər üsul və ya əhatə dairəsi dəyişmədən irəliləməyə davam etdi. Bu, paradiqmanın əsas dəyişikliyi idi, çünki həqiqi ədədləri xətt parçalarının uzunluqları kimi təyin etmək əvəzinə, o, nöqtələrin ədədlərdən (onların koordinatlarından) ibarət təsvirindən cəbrdə və daha sonra kalkulusda həndəsi məsələlərdə istifadə etməyə imkan yaradırdı. Bu parçalanmış həndəsə yalnız metodları ilə fərqlənən iki hissəyə: sırf həndəsi üsullardan istifadə edən sintetik həndəsəyə və koordinat sistemindən istifadə edən analitik həndəsəyə bölünür.

Analitik həndəsə yeni fiqurların, xüsusən də çevrə və xətlərlə əlaqəli olmayan əyrilərin öyrənilməsinə imkan verir; bu əyrilər ya funksiyaların qrafiki (tədqiqi diferensial həndəsəni doğurmuşdur) kimi, ya da məchullu tənliklər, çox vaxt polinomial tənliklər (cəbri həndəsənin doğurub) ilə müəyyən edilir. Analitik həndəsə artıq fiziki fəzanın modeli olmayan üçdən böyük fəza ölçülərini (üçdən artıq koordinatı nəzərə almaq kifayətdir) nəzərə almağa imkan verir.

19-cu əsrdə həndəsə sürətlə genişləndi. 19-cu əsrin ikinci yarısındakı böyük hadisə isə paralellik postulatının imtina olunduğu qeyri-Evklid həndəsələrinin meydana çıxması idi. Bu, Rassel paradoksu ilə yanaşı, yuxarıda qeyd olunan postulatın doğruluğunu şübhə altına almaqla riyaziyyatın təməl böhranının başlanğıc nöqtələrindəndir. Böhranın bu cəhəti aksiomatik metodun sistemləşdirilməsi və seçilmiş aksiomların doğruluğunun riyazi problem olmadığını qəbul etməklə həll edilmişdir. Öz növbəsində, aksiomatik üsul ya aksiomların dəyişdirilməsi, ya da fəzanın xüsusi çevrilmələri zamanı invariant olan xassələri nəzərə almaqla əldə edilən müxtəlif həndəsələrin öyrənilməsinə imkan verir. Bu, həndəsənin bir sıra alt sahələri və ümumiləşdirmələri ilə nəticələnir:

16-cı əsrdə Jerar Dezarq tərəfindən irəli sürülən proyektiv həndəsə, paralel xətlərin kəsişdiyi sonsuzluq nöqtələrini daxil edərək Evklid həndəsəsini genişləndirir. Bu, kəsişən və paralel xətlərə fərqli yanaşmadan boyun qaçırmaqla, klassik həndəsənin bir çox aspektlərini sadələşdirməyə imkan verir.

• Affin həndəsə, paralelliyə nəzərən və uzunluq anlayışından asılı olmayan xassələrin öyrənilməsi ilə məşğul olur.
• Diferensial həndəsə, diferensiallanan funksiyalardan istifadə etməklə müəyyən edilən əyrilərin, səthlərin və onların ümumiləşdirilməsini öyrənir.
• Çoxobrazlılar nəzəriyyəsi, mütləq daha böyük bir fəzaya uymayan formaları öyrənir.
• Riman həndəsəsi, əyri fəzalarda məsafə xassələrinin öyrənir.
• , polinomlardan istifadə etməklə müəyyən edilən əyrilərin, səthlərin və onların ümumiləşdirilməsini tədqiq edir.
• Topologiya, kəsilməz deformasiyalara məruz qalan xüsusiyyətləri öyrənir.
• , topologiyada cəbri üsulların, əsasən homoloji cəbrin istifadəsi ilə məşğul olur.
• , həndəsədə sonlu konfiqurasiyaları öyrənir.
• , qabarıq çoxluqları öyrənir, o öz əhəmiyyətini optimallaşdırmadakı tətbiqlərindən alır.
• , həqiqi ədədləri kompleks ədədlərlə əvəz etməklə əldə edilən həndəsədir.

Həndəsədə rast gəlinən bəzi fiqurlar

Üçbucaq				Toroid	Fraktal

Cəbr

Kvadratik düstur bütün kvadrat tənliklərin həllərini yığcam şəkildə ifadə edir

Cəbrə tənlik və düsturlar üzərində əməllər aparma sənəti kimi baxmaq olar. (III əsr) və Əl-Xarəzmi (IX əsr) cəbrin iki əsas carçısı idi. Birincisi, naməlum natural ədədlər (yəni tənliklər) arasındakı bəzi əlaqələri həllini əldə edənə qədər yeni əlaqələr çıxarmaqla həll etdi. İkincisi, tənlikləri çevirmək üçün sistematik üsulları təqdim etdi (məsələn, bir termini tənliyin bir tərəfindən digər tərəfə köçürmək). Cəbr termini onun əsas traktatının başlığında bu üsullardan birini adlandırmaq üçün istifadə etdiyi ərəb sözü əl-Cəbrdən əmələ gəlmişdir. "Kitab əl-cəbr vəl-mükəbala" ("Bərpa və qarşıqoyma haqqında kitab") əsərinin ərəbcə adından götürülmüş "əl-cəbr" sözü vaxt keçdikcə hamıya yaxşı məlum olan "cəbr" sözünə çevrildi. Əl-Xarəzminin bu əsəri isə tənliklərin həlli haqqında elmin yaranmasında istinad nöqtəsi oldu Əl-Xarəzminin bu əsəri isə tənliklərin həlli haqqında elmin yaranmasında istinad nöqtəsi oldu

Əl-Xarəzminin əsərində naməlum kəmiyyətlər və eləcə də aralıq çıxarışlar və tənliklərdəki çevirmələr sözlərlə ifadə olunmuşdur. Ümumiyyətlə, cəbrin başlanğıc inkişaf dövrləri üçün xarakterik olan bu cür yazı stilini tarixçilər ritorik stil adlandırırlar (xatırladaq ki, ritorika — natiqlik məharəti deməkdir).

Cəbrdə növbəti böyük sıçrayış 16-cı əsrin fransız alimi Fransua Viyetin adı ilə bağlıdır. Riyaziyyatçılar arasında ilk dəfə o məchul kəmiyyətləri və kəmiyyətlərin əmsallarını hərflərlə ifadə etmişdir. Məchul kəmiyyətlərin latın əlifbasının son hərfləri x, y, z ilə işarə olunması ənənəsinə görə isə Viyetin həmvətənlisi Rene Dekarta borcluyuq.

19-cu əsrə qədər cəbr əsasən, hazırda xətti cəbr adlanan xətti tənliklərin və cəbri tənliklər adlanan bir naməlumda cəbri tənliklərin öyrənilməsindən ibarət idi (birmənalı olmasa da, hələ də istifadə olunan bir termin). 19-cu əsrdə dəyişənlər ədədlərdən başqa (məsələn, matrislər, modul tam ədədlər və həndəsi çevrilmələr) bəzi əməllərin işləyə biləcəyi, çox vaxt hesab əməllərinin ümumiləşdirilmələrini təmsil etməyə başladı. Bununla məşğul olmaq üçün elementləri müəyyən edilməmiş çoxluqdan, çoxluğun elementləri üzərində hərəkət edən əməllərdən və bu əməllərin əməl etməli olduğu qaydalardan ibarət olan cəbri struktur anlayışı təqdim edilmişdir. Beləliklə, cəbrin əhatə dairəsi mahiyyətcə cəbri strukturların öyrənilməsinə çevrildi. Cəbrin bu obyekti müasir cəbr və ya mücərrəd cəbr adlanırdı, sonuncu termin hələ də əsasən təhsil kontekstində, düsturlarla manipulyasiyanın köhnə üsulu ilə əlaqəli elementar cəbrə qarşı istifadə olunur.

Rubik kubu: onun mümkün hərəkətlərinin öyrənilməsi qrup nəzəriyyəsinin konkret tətbiqidir

Cəbri strukturların bəzi növləri riyaziyyatın bir çox sahələrində faydalı və çox vaxt fundamental xüsusiyyətlərə malikdir. Onların tədqiqatı bu gün cəbrin muxtar hissələridir, bunlara aşağıdakılar daxildir:

• qrup nəzəriyyəsi;
• sahə nəzəriyyəsi;
• vektor fəzaları, öyrənilməsi mahiyyətcə xətti cəbrlə eynidir;
• halqa nəzəriyyəsi;
• kommutativ cəbr, kommutativ halqaları öyrənir, polinomların öyrənilməsini əhatə edir və cəbri həndəsənin təməl bölümüdür;
• homoloji cəbr
• Li cəbri və Li qrup nəzəriyyəsi;
• Bul cəbri, hansı ki, kompüterlərin məntiqi strukturunun öyrənilməsi üçün geniş istifadə olunur.

Cəbri strukturların riyazi obyektlər kimi öyrənilməsi universal cəbr və kateqoriyalar nəzəriyyəsinin obyektidir. Sonuncu hər bir riyazi struktura aiddir (yalnız cəbri olanlara deyil). Mənşəyində o, topoloji fəzalar kimi qeyri-cəbr obyektlərinin cəbri tədqiqinə imkan vermək üçün homoloji cəbrlə birlikdə təqdim edilmişdir; bu xüsusi tətbiq sahəsi cəbri topologiya adlanır.

Riyazi analiz

Əvvəllər sonsuz kiçilənlər hesabı adlanan diferensial və inteqral hesabı (lat. calculus) 17-ci əsrdə Nyuton və Leybnis tərəfindən müstəqil olaraq eyni vaxtda tərtib edilmişdir. Bu , əsasən biri digərindən asılı olan iki dəyişən kəmiyyətin əlaqəsinin öyrənilməsidir. Hesablama 18-ci əsrdə Eyler tərəfindən funksiya anlayışının tətbiqi və bir çox başqa nəticələrlə genişləndi. Hal-hazırda "diferensial və inteqral hesabı" əsasən bu nəzəriyyənin elementar hissəsinə aiddir və adətən inkişaf etmiş hissələr üçün "analiz" sözündən istifadə olunur.

Analiz daha sonra dəyişənlərin həqiqi ədədləri təmsil etdiyi real analizə və dəyişənlərin mürəkkəb ədədləri təmsil etdiyi kompleks analizə bölünür. Hal-hazırda analizin bir çox alt sahələri var, bəziləri riyaziyyatın digər sahələri ilə paylaşılır; bunlara daxildir:

• Çoxdəyişənli diferensial və inteqral hesabı
• Funksional analiz, burada dəyişənlər müxtəlif funksiyaları təmsil edir;
• İnteqrallama, ölçü nəzəriyyəsi və potensial nəzəriyyə, hamısı ehtimal nəzəriyyəsi ilə sıx bağlıdır;
• Adi diferensial tənliklər;
• Xüsusi törəməli diferensial tənliklər;
• Ədədi analiz, əsasən riyaziyyatın bir çox tətbiqlərində yaranan adi və xüsusi törəməli diferensial tənliklərin həllərinin kompüterlərdə hesablanmasına həsr edilmişdir.

Diskret riyaziyyat

Diskret riyaziyyat istər riyaziyyatın özündə və istərsə də onun tətbiqində əmələ gələn diskret strukturların xassələrini öyrənən bölmədir. Bununla belə ən mühüm xarakteristikaları sonlu və ya hesabi qiymətlər alan obyektlər diskret strukturlar adlanır. Belə strukturlar sırasına məsələn, sonlu qruplar, sonlu qraflar, informasiyaları dəyişdirən bəzi riyazi modellər, sonlu avtomatlar, aiddir. Bu fınit (sonlu) xarakterli strukturlara misallardır. Diskret riyaziyyatın onları öyrənən bölməsi bəzən sonlu (fınit) riyaziyyat adlanır. Finit strukturlardan başqa diskret riyaziyyatda həm də sonsuz diskret strukturlar (məsələn, sonsuz cəbri sistemlər, sonsuz qraflar, sonsuz avtomatlar) öyrənilir.

Diskret riyaziyyatın elementləri çox qədimdən məlumdur: riyaziyyatın başqa bölmələri ilə paralel inkişaf edərək, onların tərkib hissəsi olmuşdur. Tam ədədlərin xassələri ilə əlaqədar məsələlər səciyyəvidir, sonralar bu məsələlər ədədlər nəzəriyyəsinin yaranmasına gətirib çıxarmışdır. Diskret riyaziyyatın inkişafının bu mərhələsi Diofant, Evklid, Pifaqor və Eratosfenin adı ilə bağlıdır. 17–18-ci əsrlərdə, əsasən, oyun məsələləri ilə bağlı kombinator analizinin elementləri və diskret ehtimal nəzəriyyəsi əmələ gəlmişdir. 18–19-cu əsrlərdə ədədlər nəzəriyyəsi, cəbr və həndəsənin ümumi problemləri ilə əlaqədar olaraq əslində diskret təbiətə malik olan cəbrin mahiyyətini və gələcək inkişafını təyin edən qrup, meydan və halqa kimi mühüm anlayışlar meydana çıxmışdır. 17–19-cu əsrlər ərzində diskret riyaziyyatın inkişafı K. Abel. E. Varinq, V. Hamilton, E. Qalua, A. Keli, J. Laqranj, A. Lejandr, P. Ferma və E. Eylerin adları ilə bağlıdır. 19–20-ci əsrlərdə riyazi düşüncələrin ciddiliyinə meyillik və riyaziyyat metodlarının analizi daha bir bölmənin — riyazi məntiqin ayrılmasına gətirmişdir. Bu zaman diskret riyaziyyatın problemləri ilə L. Brauer, C. Bul, N. Viner, K. Gödel. D. Hilbert, A. Çörç, K. Şennon məşğul olmuşlar.

XX əsrdə diskret riyaziyyatın inkişafına, əsasən, praktik ehtiyaclar səbəb olmuşdur. Müxtəlif problemləri riyazi metodlarla öyrənən yeni elm — kibernetika və onun nəzəri hissəsi olan meydana gəldi. Riyazi kibernetika diskret riyaziyyatın ideya və məsələlərinin bir növ təchizedənidir. Belə ki, böyük hesablamalar tələb edən tətbiqi məsələlər, onların həlli üçün hesablama üsullarının yaradılmasını və inkişafını stimullaşdırdı ki, bu da hesablama riyaziyyatının yaranmasına və inkişafına səbəb oldu. "Hesablama" və "alqoritm" anlayışlarının analizi alqoritmlər nəzəriyyəsinin yaranmasına gətirdi. İnformasiyaların saxlanması, işlənməsi və ötürülməsi məsələləri informasiyalar nəzəriyyəsi, kodlaşdırma nəzəriyyəsi və nəzəri kriptoqrafiyanın meydana gəlməsinə kömək etmişdir. Riyaziyyatın daxili problemləri ilə yanaşı, iqtisadi və elektrotexnika məsələləri, qraflar nəzəriyyəsinin inkişafını tələb etdirdi. İşin təsviri və mürəkkəb idarəetmə sistemlərinin yaradılması məsələləri idarəetmə sistemləri nəzəriyyəsi və avtomatlar nəzəriyyəsi fənnini təşkil etdi.

Riyazi məntiq və çoxluqlar nəzəriyyəsi

Bu mövzular 19-cu əsrin sonlarından etibarən riyaziyyata daxil olmuşdur. Bu dövrə qədər çoxluqlar riyazi obyektlər hesab edilmirdi və məntiqi-riyazi isbatlar üçün istifadə olunsa da, fəlsəfəyə aid edilirdi və riyaziyyatçılar tərəfindən xüsusi olaraq öyrənilmirdi.

Eyni dövrdə riyaziyyatın müxtəlif sahələrində əsas riyazi obyektlərin əvvəlki intuitiv təriflərinin riyazi ciddiliyi təmin etmək üçün kifayət etmədiyi ortaya çıxdı. Bu cür intuitiv təriflərə misal olaraq "çoxluq obyektlərin toplusudur", "natural ədəd sayma üçün istifadə olunan şeydir", "nöqtə bütün istiqamətlərdə sıfır uzunluğa malik formadır", "əyri hərəkət edən nöqtənin buraxdığı izdir" və s.

Bu, riyaziyyatın əsaslı böhranının mənşəyidir. Nəhayət, rəsmiləşdirilmiş çoxluq nəzəriyyəsi daxilində aksiomatik metodu sistemləşdirməklə riyaziyyatın əsas axınında həll edilmişdir. Kobud desək, hər bir riyazi obyekt bütün oxşar obyektlərin çoxluğu və bu obyektlərin malik olmalı olduğu xassələrlə müəyyən edilir. Məsələn, Peano arifmetikasında natural ədədlər "sıfır ədəddir", "hər bir ədəd unikal varisidir", "sıfırdan başqa hər bir ədədin özünəməxsus sələfi var" və bəzi mülahizə qaydaları ilə müəyyən edilir. Bu şəkildə müəyyən edilən obyektlərin "təbiəti" riyaziyyatçıların filosoflara buraxdığı fəlsəfi problemdir, hətta bir çox riyaziyyatçının bu təbiətlə bağlı fikirləri olduğu və öz rəylərindən — bəzən "intuisiya" da deyilən — araşdırma və sübut tapmaq üçün istifadə edirlər.

Bu yanaşma "məntiqləri" (yəni icazə verilən çıxarış qaydaları toplusunu), teoremləri, isbatları və s.-ni riyazi obyektlər hesab etməyə və onlar haqqında teoremləri isbat etməyə imkan verir. Məsələn, Gödelin natamamlıq teoremləri, kobud desək, təbii ədədləri ehtiva edən hər bir nəzəriyyədə doğru olan (daha geniş nəzəriyyədə isbat oluna bilən), lakin nəzəriyyə daxilində isbat olunmayan teoremlərin olduğunu iddia edir.

Riyaziyyatın əsaslarına bu cür yanaşma 20-ci əsrin birinci yarısında L. E. J. Brauerin rəhbərliyi altındakı riyaziyyatçılar orta qanunu istisna edən intuisiya məntiqini irəli sürmüşdür.

Bu problemlər və mübahisələr model nəzəriyyəsi (bəzi məntiqi nəzəriyyələrin digər nəzəriyyə daxilində modelləşdirilməsi), isbat nəzəriyyəsi, tip nəzəriyyəsi, hesablama nəzəriyyəsi və hesablamalı komplekslik nəzəriyyəsi kimi alt sahələrlə riyazi məntiqin xeyli genişlənməsinə səbəb oldu. Riyazi məntiqin bu aspektləri kompüterlərin yaranmasından əvvəl təqdim olunsa da, onların kompilyator dizaynında, proqramların sertifikatlaşdırılmasında, interaktiv isbat alətlərində və kompüter elminin digər aspektlərində istifadəsi öz növbəsində bu məntiqi nəzəriyyələrin genişlənməsinə töhfə verdi.

Tətbiqi riyaziyyat

Tətbiqi riyaziyyat, adətən, elm, mühəndislik, biznes və sənayedə istifadə olunan riyazi metodlarla məşğul olur. Beləliklə, "tətbiqi riyaziyyat" xüsusi ixtisaslaşmış riyaziyyat elmidir. Tətbiqi riyaziyyat termini həm də riyaziyyatçıların praktiki məsələlərlə məşğul olduğu peşəkar ixtisası təsvir edir; praktiki məsələlərə diqqət yetirən bir peşə kimi tətbiqi riyaziyyat elm, mühəndislik və riyazi praktikanın digər sahələrində "riyazi modellərin formalaşdırılması, öyrənilməsi və istifadəsi"nə diqqət yetirir.

Keçmişdə praktik tətbiqlər riyazi nəzəriyyələrin inkişafına təkan vermiş, daha sonra ilk növbədə riyaziyyatın öz məqsədləri üçün inkişaf etdirdiyi saf riyaziyyatda öyrənmə mövzusuna çevrilmişdir. Beləliklə, tətbiqi riyaziyyatın fəaliyyəti saf riyaziyyatda aparılan tədqiqatlarla həyati şəkildə bağlıdır.

Statistika və digər qərar qəbuletmə elmləri

Tətbiqi riyaziyyat, nəzəriyyəsi riyazi şəkildə formalaşan statistika fənni ilə, xüsusən, ehtimal nəzəriyyəsi ilə əhəmiyyətli dərəcədə uzlaşır. Statistiklər (tədqiqat layihəsinin bir hissəsi kimi işləyirlər) təsadüfi seçim və sınaqların köməyilə "məntiqli məlumat yaradırlar"; statistik nümunə və ya sınaq layihələndirmə məlumatlarının təhlilini müəyyən edir (məlumatlar əlçatan olmamışdan əvvəl). Eksperimentlərdən və nümunələrdən əldə edilən məlumatları yenidən nəzərdən keçirərkən və ya müşahidə tədqiqatlarından əldə edilən məlumatları təhlil edərkən statistiklər modelləşdirmə sənətindən və qərar qəbul etmə nəzəriyyəsindən istifadə edərək "verilənlərə məna yükləyirlər" — model seçimi və qiymətləndirilməsi ilə; təxmin edilən modellər və ardıcıl proqnozlar yeni məlumatlar üzərində sınaqdan keçirilməlidir.

Statistik nəzəriyyə statistik fəaliyyət riskini (gözlənilən itkini) minimallaşdırılması kimi qərar qəbuletmə problemlərini, məsələn, parametrlərin qiymətləndirilməsi, fərziyyələrin yoxlanılması və ən yaxşısının seçilməsi kimi problemləri öyrənir. Riyazi statistikanın bu ənənəvi sahələrində statistik qərar problemi müəyyən məhdudiyyətlər altında gözlənilən itki və ya xərc kimi məqsəd funksiyalarını minimuma endirməklə formulə edilir: Məsələn, sorğunun tərtib edilməsi çox vaxt verilmiş güvən səviyyəsi göstəricisi ilə əhalinin orta dəyərini qiymətləndirmək xərclərinin minimuma endirilməsini nəzərdə tutur. Optimallaşdırmadan istifadə etdiyinə görə, statistikanın riyazi nəzəriyyəsi əməliyyatlar tədqiqi, idarəetmə nəzəriyyəsi və riyazi iqtisadiyyat kimi digər qərar qəbuletmə elmləri ilə ortaq maraq dairəsinə malikdir.

Hesablama riyaziyyatı

Hesablama riyaziyyatı insanın ədədi qabiliyyəti üçün adətən çox böyük olan riyazi problemlərin həlli üsullarını təklif edir və öyrənir. Ədədi analiz, funksional analiz və yaxınlaşma nəzəriyyəsindən istifadə edərək təhlildə problemlərin həlli üsullarını öyrənir; ədədi analiz geniş şəkildə yuvarlaqlaşdırma xətalarına xüsusi diqqət yetirməklə yaxınlaşma və diskretləşdirmənin öyrənilməsini əhatə edir. Ədədi analiz və daha geniş mənada elmi hesablama da riyaziyyat elminin analitik olmayan mövzularını, xüsusən alqoritmik-matris və qrafik nəzəriyyəsini öyrənir. Hesablama riyaziyyatının digər sahələrinə kompüter cəbri və simvolik hesablama daxildir.

Riyazi fizika	Hidroaeromexanika	Riyazi analiz	Optimallaşdırma	Ehtimal nəzəriyyəsi	Statistika
Riyazi maliyyə	Oyunlar Nəzəriyyəsi	Riyazi biologiya	Riyazi kimya	Riyazi iqtisadiyyat	İdarəetmə nəzəriyyəsi

Tarix

Riyaziyyat tarixinə daim artan abstraksiyalar silsiləsi kimi baxmaq olar. Təkamül baxımından desək, bir çox heyvanlar tərəfindən paylaşılan ilk abstraksiya, ehtimal ki, ədədlərlə bağlı idi: iki alma kolleksiyasının və iki portağal kolleksiyasının (məsələn) ortaq bir şeyin olduğunun fərqinə varılması, yəni üzvlərinin sayı. Sümükdə tapılan rəqəmlərin sübut edildiyi kimi, tarixdən əvvəlki insanlar fiziki obyektlərin necə hesablanacağını bilməklə yanaşı, vaxt, günlər, fəsillər və ya illər kimi mücərrəd kəmiyyətləri də hesablamış ola bilərlər.

Babillərə məxsus riyazi lövhə Plimpton 322, eramızdan əvvəl 1800-cü ilə aiddir.

Daha mürəkkəb riyaziyyat üçün dəlillər təxminən eramızdan əvvəl 3000-ci ilə qədər, babillilər və misirlilər vergi və digər maliyyə hesablamaları, tikinti və astronomiya üçün hesab, cəbr və həndəsədən istifadə etməyə başlayanda ortaya çıxmışdır. Mesopotamiya və Misirdən gələn ən qədim riyazi mətnlər eramızdan əvvəl 2000–1800-cü illərdir. Bir çox erkən mətnlərdə Pifaqor üçlüyü qeyd olunur və nəticədə Pifaqor teoremi əsasən hesab və həndəsədən sonra ən qədim və geniş yayılmış riyazi anlayış kimi görünür. Babildə elementar hesaba (toplama, çıxma, vurma, bölmə) aid ilk arxeoloji qeydlərə rast gəlinir. Babillilər həm də "yerölçmə" sisteminə malik idilər və bucaqları və vaxtı ölçmək üçün bu gün də istifadə olunan altmışlıq say sistemindən istifadə edirdilər.

Arximed burada təsvir olunan kiçiltmə üsulundan istifadə edərək, π-nin qiymətini təqribi hesablamışdır.

Eramızdan əvvəl 6-cı əsrdən başlayaraq Qədim Yunanıstanda Pifaqorçular, həmçinin qədim yunanlar riyaziyyatı özünəməxsus fənn kimi sistemli şəkildə öyrənməyə başladılar. Təqribən eramızdan əvvəl 300-cü ildə Evklid hazırda riyaziyyatda istifadə olunan tərif, aksiom, teorem və ibatdan ibarət aksiomatik metodu təqdim etdi. Onun Başlanğıclar kitabı bütün dövrlərin ən uğurlu və effektiv dərsliyi hesab olunur. Antik dövrün ən böyük riyaziyyatçısı çox vaxt Sirakuzalı Arximed (e.ə. 287–212) hesab edilir. O fırlanma cisimlərinin səthinin sahəsini və həmini hesablamaq üçün düsturlar çıxardı və müasir diferensial və inteqral hesabından çox da fərqli olmayan üsulla sonsuz sıraların cəmindən istifadə etməklə parabolanın altındakı sahəni hesablamaq üçün kiçiltmə üsulundan istifadə etdi. Yunan riyaziyyatının digər diqqətəlayiq nailiyyətləri konik kəsiklər (Perqalı Apolloni, e.ə. 3-cü əsr), triqonometriya (Nikeili Hipparx, eramızdan əvvəl 2-ci əsr) və cəbrin başlanğıclarıdır (Diofant, eramızın III əsri).

Baxşali əlyazmasında istifadə olunan rəqəmlər eramızdan əvvəl II əsrdən eramızın II əsrinə aiddir.

Bu gün bütün dünyada istifadə edilən hindu-ərəb say sistemi və onun əməllərindən istifadə qaydaları eramızın birinci minilliyi ərzində Hindistanda inkişaf etmiş və İslam riyaziyyatı vasitəsilə Qərb dünyasına çatdırılmışdır. Hindistan riyaziyyatının digər diqqətəlayiq inkişaflarına sinus və kosinusun müasir tərifi və yaxınlaşması və sonsuz sıraların erkən forması daxildir.

əl-Xarəzminin Əl-cəbr kitabından bir səhifə

Leonardo Fibonaççi, 1-ci və 4-cü əsrlər arasında hind riyaziyyatçıları tərəfindən icad edilən hind-ərəb say sistemini Qərb dünyasına təqdim edən italyan riyaziyyatçısı.

İslamın Qızıl dövründə, xüsusilə 9-cu və 10-cu əsrlərdə riyaziyyat Yunan riyaziyyatı üzərində qurulan bir çox mühüm yeniliklərlə rastlaşdı. İslam riyaziyyatının ən diqqətçəkən nailiyyəti cəbrin inkişafı olmuşdur. İslam dövrünün digər nailiyyətləri arasında sferik triqonometriyada irəliləyişlər və ərəb say sisteminə onluq kəsri bildirən nöqtənin əlavə edilməsi daxildir. Bu dövrün bir çox görkəmli riyaziyyatçılarına Əl-Xarəzmi, Ömər Xəyyam və Nəsirəddin Tusi kimi alimlər də daxil idi.

Erkən müasir dövrdə Qərbi Avropada riyaziyyat sürətlə inkişaf etməyə başladı. 17-ci əsrdə İsaak Nyuton və Qotfrid Leybnis tərəfindən kalkulusun inkişafı riyaziyyatda inqilab yaratdı. Leonard Eyler 18-ci əsrin çoxsaylı teorem və kəşflərə töhfə verən ən görkəmli riyaziyyatçısı idi. 19-cu əsrin bəlkə də ən qabaqcıl riyaziyyatçısı cəbr, analiz, diferensial həndəsə, matris nəzəriyyəsi, ədədlər nəzəriyyəsi və statistika kimi sahələrə çoxsaylı töhfələr verən alman riyaziyyatçısı Karl Qausdur. 20-ci əsrin əvvəllərində Kurt Gödel özünün natamamlıq teoremlərini dərc edərək riyaziyyatı dəyişdirdi, hansı ki, hər hansı bir ardıcıl aksiomatik sistemin – hesabı təsvir etmək üçün kifayət qədər güclü olarsa – isbat olunmayan doğru müddəaları ehtiva edəcək.

O vaxtdan bəri riyaziyyat çox genişləndi və riyaziyyatla elm arasında qarşılıqlı səmərəli əlaqə yarandı. Riyazi kəşflər bu günə qədər davam etməkdədir. Mixail B. Sevryukun dediyinə görə, Amerika Riyaziyyat Cəmiyyətinin Bülleteninin 2006-cı il yanvar sayında "1940-cı ildən (MR-in fəaliyyətinin ilk ili) Mathematical Reviews (Riyazi İcmal) bazasına daxil edilmiş məqalə və kitabların sayı hazırda 1,9-dan çoxdur və hər il verilənlər bazasına 75 mindən çox element əlavə olunur. Bu okeandakı əsərlərin böyük əksəriyyətində yeni riyazi teoremlər və onların isbatları var."

Etimologiya

Yunan dilindəki "matematika" sözünün kökü máthēma (μάθημα) olub, bu da "öyrənilən", "öyrənilən şey", yəni "öyrənmək" və "elm" mənalarını verir. "Matematika" sözü klassik dövrdə belə daha dar və texniki mənada, "riyazi çalışma" mənasında işlənirdi. Onun sifət qarşılığı mathēmatikós (μαθηματικός), "öyrənmə ilə əlaqəli" və ya "çalışqan" mənasını verir və bu da eynilə "riyazi" mənasını verir. Xüsusilə, matēmatikḗ tékhnē (μαθηματικὴ τέχνη; latınca: ars mathematica) "riyazi məharət" mənasını verirdi.

Eynilə, Pifaqorçuluqdakı iki əsas təfəkkür məktəbindən biri mathēmatikoi (μαθηματικοί) kimi tanınırdı — o zamanlar müasir "riyaziyyatçılar" mənasını deyil, "öyrənənlər" mənasını verirdi.

Təxminən 1700-cü ilə qədər latın və ingilis dilində riyaziyyat termini daha çox "riyaziyyat" deyil, "astrologiya" (və ya bəzən "astronomiya") mənasını verirdi; indiki Məna tədricən indiki 1500-dən 1800-ə dəyişdi. Bu, bir neçə səhv tərcümə ilə nəticələndi. Məsələn, Müqəddəs Avqustinin xristianların astroloqlar mənasını verən riyaziyyatdan çəkinməli olduğu barədə xəbərdarlığı bəzən "riyaziyyatçıların qınanması" mənasında, səhv tərcümə olunur.

Fransız cəm forması les mathématiques (və daha az istifadə olunan tək törəmə la mathématique) kimi ingilis dilində görünən cəm forması yunanca ta mathēmatiká (τὰ μαθηματ) cəminə əsaslanan Latın neyter cəm riyaziyyatına (Sisero) qayıdır. Aristotel (e.ə. 384–322) tərəfindən istifadə edilmiş və təqribən "riyazi hər şey" mənasını verir, baxmayaraq ki, ingilis dilinin yalnız mathematic(al) sifətini götürməsi və fizika və metafizika nümunəsindən sonra riyaziyyat adını yenidən formalaşdırması inandırıcıdır. yunancadan miras qalmışdır. İngilis dilində riyaziyyat adı tək fel qəbul edir. Tez-tez riyaziyyata və ya Şimali Amerikada math kimi qısaldılır.

Riyaziyyat fəlsəfəsi

Riyaziyyatın dəqiq tərifi və ya epistemoloji statusu haqqında ümumi razılıq yoxdur. Aristotel riyaziyyatı "kəmiyyət elmi" kimi təyin etmiş və bu tərif 18-ci əsrə qədər məşhur olmuşdur. Bununla belə, Aristotel qeyd edirdi ki, təkcə kəmiyyətə diqqət yetirmək riyaziyyatı fizika kimi elmlərdən ayırmaya bilər; onun fikrincə, abstraksiya və kəmiyyətin real nümunələrdən "fikrən ayrıla bilən" bir xüsusiyyət kimi öyrənilməsi riyaziyyatı digərlərindən ayırır.

19-cu əsrdə riyaziyyatın tədqiqi ciddi şəkildə artdı, kəmiyyət və ölçü ilə dəqiq əlaqəsi olmayan qrup nəzəriyyəsi və proyektiv həndəsə kimi mücərrəd mövzulara toxunmağa başlayanda riyaziyyatçılar və filosoflar müxtəlif yeni təriflər verməyə başladılar.

Peşəkar riyaziyyatçıların çoxu riyaziyyatın tərifi ilə maraqlanmır və ya onu qeyri-müəyyən hesab edir. Hətta riyaziyyatın sənət və ya elm olması ilə bağlı ortaq bir qərar yoxdur. Bəziləri sadəcə deyirlər ki, "riyaziyyat riyaziyyatçıların işidir".

Üç aparıcı növ

Bu gün riyaziyyatın öndə gələn üç yanaşma növü, , və formalist adlanır və hər biri fərqli bir fəlsəfi düşüncə məktəbini əks etdirir. Bunların hamısının ciddi qüsurları var, heç biri geniş şəkildə qəbul edilmir və heç bir uzlaşma mümkün görünmür.

Logisist təriflər

Riyaziyyatın məntiq baxımından ilk tərifi (1870) idi. O riyaziyyatı "lazımi nəticələr çıxaran elm" adlandırırdı. Principia Mathematica'da Bertran Rassel və Alfred Nort Vaythed məntiq kimi tanınan fəlsəfi proqramı irəli sürdülər və bütün riyazi anlayışların, müddəaların və prinsiplərin tamamilə simvolik məntiq baxımından müəyyən edilə və isbat oluna biləcəyini sübut etməyə çalışdı. Riyaziyyatın məntiqi tərifinə misal olaraq "Riyaziyyat bütövlükdə simvolik məntiqdir" (1903) əsəridir.

İntuisionist təriflər

Riyaziyyatçı L. E. J. Brauerin fəlsəfəsindən irəli gələn intuisioist təriflər riyaziyyatı müəyyən zehni proseslərlə eyniləşdirir. İntuisionist tərifərə misal olaraq "Riyaziyyat bir-birinin ardınca konstruksiyaların həyata keçirilməsindən ibarət olan zehni fəaliyyətdir". özəlliyi ondan ibarətdir ki, o, digər təriflərə görə etibarlı hesab edilən bəzi riyazi fikirləri rədd edir.

Xüsusilə, digər riyaziyyat fəlsəfələri inşa edilə bilməsələr də mövcudluğu sübuta yetirilə bilən obyektlərə icazə versə də, intuitivizm yalnız insanın həqiqətən qura biləcəyi riyazi obyektlərə icazə verir. İntuisiyaçılar da xaric edilmiş orta qanunu rədd edirlər (məsələn, ${\displaystyle {\displaystyle P\vee \neg P}}$). Baxmayaraq ki, bu mövqe onları uyğun sübut metodu kimi ziddiyyətli sübutun ümumi bir variantını, yəni ${\displaystyle {\displaystyle \neg P\to \bot }}$-dən ${\displaystyle P}$-nin çıxarmasını rədd etməyə məcbur edir. Bu mövqe onları ziddiyyətli sübutun ümumi bir variantını, yəni ${\displaystyle {\displaystyle P\to \bot }}$-dən ${\displaystyle \neg P}$-nin çıxarışını ala bilərlər. Onlar üçün ${\displaystyle {\displaystyle \neg (\neg P)}}$ ${\displaystyle P}$-dən daha zəif ifadədir.

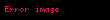
Formalist təriflər

Formalist təriflər riyaziyyatı simvollar və onların üzərində əməlaparma qaydaları ilə müəyyən edir. riyaziyyatı sadəcə olaraq "formal sistemlər elmi" kimi təyin etmişdir. Rəsmi sistem simvollar və ya işarələr toplusudur və simvolların düsturlara necə birləşdiriləcəyinə dair bəzi qaydalardır. Formal sistemlərdə aksiom sözü "öz-özünə aşkar olan həqiqət" kimi adi mənadan fərqli xüsusi məna daşıyır və sistemin qaydaları müəyyən bir formal sistemə daxil olan işarələrin birləşməsinə istinad etmək üçün istifadə olunur.

Riyaziyyat elm kimi

Karl Fridrix Qauss, riyaziyyatçıların şahı kimi tanınır

Alman riyaziyyatçısı F. Qauss riyaziyyatı "elmlərin şahı" adlandırırdı. Bu yaxınlarda Markus du Sautoy riyaziyyatı "elmin şahı… elmi kəşfin arxasında duran əsas hərəkətverici qüvvə" adlandırdı. Filosof Karl Popper qeyd edirdi ki, "riyazi nəzəriyyələrin çoxu fizika və biologiyanın nəzəriyyələri kimi hipotetiko-deduktivdir: buna görə də saf riyaziyyat fərziyyələri olan təbiət elmlərinə son zamanlar daha yaxın görünür". Popper həmçinin qeyd etmişdir ki, "Mən bir sistemin təcrübi və ya elmi olduğunu, o halda qəbul edəcəyəm ki, o, təcrübə ilə sınaqdan keçirilə bilsin".

Riyaziyyat fiziki elmlərin bir çox sahələri ilə, xüsusən də fərziyyələrin məntiqi nəticələrinin tədqiqi ilə çox oxşardır. İntuisiya və eksperimentasiya həm riyaziyyatda, həm də (digər) elmlərdə fərziyyələrin formalaşmasında da rol oynayır. Eksperimental riyaziyyatın riyaziyyat daxilindəki əhəmiyyəti artmaqda davam edir və hesablama və simulyasiya həm elmlərdə, həm də riyaziyyatdakı rolu getdikcə artır.

Bir sıra müəlliflər hesab edirlər ki, riyaziyyat bir elm deyil, çünki o, empirik dəlillərə əsaslanmır. Bu mövzuda riyaziyyatçıların fikirləri müxtəlifdir. Bir çox riyaziyyatçılar hesab edirlər ki, öz sahələrini elm adlandırmaq onun estetik tərəfinin əhəmiyyətini və ənənəvi yeddi liberal sənətdə tarixini azaltmaq deməkdir; başqaları hesab edirlər ki, onun elmlərlə əlaqəsinə məhəl qoymamaq riyaziyyat və onun elm və mühəndislikdəki tətbiqləri arasındakı interfeysin riyaziyyatda çoxlu inkişafa səbəb olduğuna göz yummaqdır. Bu baxış fərqinin ortaya çıxmasının bir yolu, riyaziyyatın yaradıldığı (sənətkarlıqda olduğu kimi) və ya kəşf edildiyi (elmdə olduğu kimi) ilə bağlı fəlsəfi mübahisələrdədir. Praktikada riyaziyyatçılar, adətən, ümumi səviyyədə alimlərə görə qruplaşdırılır, lakin daha incə səviyyələrdə ayrılırlar. Bu, riyaziyyat fəlsəfəsində nəzərdən keçirilən çoxsaylı məsələlərdən biridir.

Abstrakt idrak

Riyaziyyat müxtəlif çoxsaylı problemlər üzündən meydana çıxmışdır. Əvvəlcə bunlar ticarət, torpaq ölçmə, memarlıq və daha sonra

İsaak Nyuton (solda) və Qotfrid Vilhelm Leybnis sonsuz kiçilənlər hesabını yaratmışlar.

astronomiyayla bağlı idi; bu gün bütün elmlər riyaziyyat üçün problemlər irəli sürür, bir çox problemlər də riyaziyyatın öz daxilində ortaya çıxır. Məsələn, fizik Riçard Feynman riyazi mülahizə və fiziki anlayışın birləşməsindən istifadə edərək kvant mexanikasının trayektoriya-inteqral formulyasiyasını icad etdi və riyaziyyat bugünkü sim nəzəriyyəsinə, təbiətin dörd fundamental qüvvəsini birləşdirməyə cəhd edən, lakin hələ də təkmilləşməkdə olan elmi nəzəriyyəyə ilham verməkdə davam edir.

Bəzi riyaziyyatlar yalnız onu ilhamlandıran sahəyə aiddir və bu sahədə gələcək problemlərin həlli üçün tətbiq olunur. Ancaq çox vaxt bir sahədən ilhamlanan riyaziyyat bir çox sahələrdə faydalı olduğunu sübut edir və riyazi anlayışların ümumi fonduna qoşulur. Çox vaxt saf riyaziyyat və tətbiqi riyaziyyat arasında fərq qoyulur. Bununla belə, saf riyaziyyat mövzuları çoxlu tətbiqlərə malikdir. Məsələn, kriptoqrafiyada ədədlər nəzəriyyəsi tətbiq olunur.

Bu diqqətəlayiq fakt, hətta "ən saf" riyaziyyatın da çox vaxt praktik tətbiqlərə malik olduğunu ortaya qoyur. Fizik Yucin Viqner bu fenomeni "riyaziyyatın ağlasığmaz effektivliyi" adlandırır. Riyaziyyat fəlsəfəçisi Mark Steyner bu mövzuda geniş yazıb və etiraf edir ki, riyaziyyatın tətbiq oluna bilməsi "naturalizm üçün bir problemdir". Riyaziyyat fəlsəfəçisi Meri Lenq üçün fiziki dünyanın kainatın hüdudlarından kənarda mövcud olan səbəbsiz riyazi varlıqların diktəsinə uyğun hərəkət etməsi "xoş təsadüfdür". Digər tərəfdən, bəzi antirealistlər üçün riyazi şeylər arasında əldə edilən əlaqələr kainatdakı cisimlər arasında əldə edilən əlaqələri əks etdirir, buna görə də "xoş təsadüf" yoxdur.

Əksər tədqiqat sahələrində olduğu kimi, elm dövründə də bilik partlayışı ixtisaslaşmaya gətirib çıxardı: indi riyaziyyatda yüzlərlə ixtisaslaşmış sahə var və riyaziyyatın bölmələr üzrə ən son təsnifatı 46 səhifədən ibarətdir. Hətta tətbiqi riyaziyyatın bir neçə sahəsi praktik sahələrlə birləşərək statistika, əməliyyatlar tədqiqi və kompüter elmi kimi müstəqil fənlərə çevrilmişdir.

Riyaziyyata meyilli olanlar üçün çox vaxt riyaziyyatın müəyyən bir estetik tərəfi var. Bir çox riyaziyyatçılar riyaziyyatın zərifliyindən, onun daxili estetikasından və daxili gözəlliyindən danışır, onun sadəliyini və ümumiliyini təqdir edirlər. Evklidin sonsuz sayda sadə ədədlər olduğunu isbat etməsi kimi sadə və zərif bir isbatda və sürətli Furye çevrilməsi kimi hesablamanı sürətləndirən zərif ədədi üsulda gözəllik var. Q. H. Hardi Riyaziyyatçının üzrxahlığı əsərində bu estetik mülahizələrin özlüyündə saf riyaziyyatın öyrənilməsinə haqq qazandırmaq üçün yetərli olduğuna inamını ifadə etmişdir. Əhəmiyyətlilik, gözlənilməzlik, qaçılmazlıq və qənaət kimi meyarları riyazi estetikaya töhfə verən amillər kimi müəyyən etmişdir. Riyazi tədqiqat çox zaman riyazi obyektin kritik xüsusiyyətlərini axtarır. Bu xüsusiyyətlərlə obyektin səciyyələndirilməsi kimi ifadə edilən teorem mükafatdır. Xüsusilə yığcam və aşkar riyazi arqumentlərin nümunələri və tərəfindən Kitabdan isbatlar kitabında dərc edilmişdir.

Əyləncəli riyaziyyatın populyarlığı bir çoxlarının riyazi sualları həll etməkdən həzz aldığının başqa bir əlamətidir. Digər sosial ekstremallıqda isə filosoflar riyaziyyat fəlsəfəsində riyazi isbatın təbiətinə oxşar olaraq problemlər tapmağa davam edirlər.

İşarələmələr, dil və ciddilik

Leonard Eyler bu gün istifadə olunan riyazi işarələrin bir çoxunu yaratmış və populyarlaşdırmışdır.

Bu gün istifadə olunan riyazi qeydlərin əksəriyyəti 16-cı əsrə qədər icad edilmişdir. Bundan əvvəl riyaziyyat riyazi kəşfləri məhdudlaşdıran sözlərlə yazılırdı. Eyler (1707–1783) bu gün istifadə olunan bir çox işarələri irəli sürmüşdür. Müasir işarələr riyaziyyatı peşəkarlar üçün çox asanlaşdırır, lakin yeni başlayanlar çox vaxt bunu çətin hesab edirlər. görə, bunu riyazi fikirlərin təbii dildən daha mücərrəd və daha çox şifrəli olması ilə əlaqələndirmək olar. İnsanların tez-tez sözü uyğun gələn fiziki obyektlə (məsələn, inək) eyniləşdirə bildiyi təbii dildən fərqli olaraq, riyazi simvollar mücərrəddir və heç bir fiziki analoqu yoxdur. Riyazi simvollar həm də adi sözlərdən daha yüksək şifrələnir, yəni bir simvol bir sıra müxtəlif əməlləri və ya fikirləri kodlaya bilər.

Riyazi dili başa düşmək yeni başlayanlar üçün çətin ola bilər, çünki hətta və ya və yalnız kimi ümumi terminlər gündəlik nitqdə olduğundan daha dəqiq məna daşıyır və açıq və sahə kimi digər terminlər onların əhatə etmədiyi xüsusi riyazi ideyalara istinad edir. Laymen mənaları Riyaziyyat dilinə homeomorfizm və inteqrasiya kimi riyaziyyatdan kənar mənası olmayan bir çox texniki terminlər də daxildir. Bundan əlavə, "ancaq və ancaq" üçün iff ("if and only if") kimi qısa ifadələr riyazi jarqona aiddir. Xüsusi işarələrin və texniki lüğətin səbəbi var: riyaziyyat gündəlik nitqdən daha çox dəqiqlik tələb edir. Riyaziyyatçılar dil və məntiqin bu dəqiqliyinə "ciddilik" deyirlər.

Riyazi sübutların etibarlılığı prinsipcə ciddilik məsələsidir. Riyaziyyatçılar öz teoremlərinin sistematik mülahizə vasitəsilə aksiomlardan irəli gəlməsini istəyirlər. Bu, mövzunun tarixində bir çox halları baş vermiş səhv intuisiyalara əsaslanan səhv "teoremlərdən" uzaqlaşmaq üçündür. Riyaziyyatda gözlənilən sərtlik səviyyəsi zamanla dəyişdi: yunanlar ətraflı arqumentlər gözləyirdilər, lakin İsaak Nyutonun dövründə tətbiq olunan üsullar daha az ciddilikdə idi. Nyutonun istifadə etdiyi təriflərə xas olan problemlər 19-cu əsrdə diqqətli təhlilin və formal isbatların yenidən canlanmasına səbəb olardı. Riyaziyyatın səhv başa düşülməsi riyaziyyatın bəzi ümumi yanlış təsəvvürlərinin diqqətəlayiq səbəbidir. Bu gün riyaziyyatçılar kompüterin köməyi ilə isbatlar haqqında öz aralarında mübahisə etməyə davam edirlər. Böyük hesablamaları yoxlamaq çətin olduğundan, istifadə olunan kompüter proqramı səhv olarsa, bu cür sübutlar səhv ola bilər. Digər tərəfdən, isbat alətləri əl ilə yazılmış isbatda verilə bilməyən bütün detalların yoxlanılmasına imkan yaradır və Feyt-Tompson teoremi kimi uzun isbatların düzgünlüyünə əminlik verir.

Ənənəvi olaraq aksiomlar "öz-özünə aydın olan həqiqətlər" kimi düşünülürdü, lakin bu fikir problemlidir. Formal səviyyədə aksiom yalnız aksiomatik sistemin bütün törəmə düsturları kontekstində daxili məna daşıyan simvollar silsiləsidir. Hilbertin proqramının məqsədi bütün riyaziyyatı möhkəm aksiomatik əsaslar üzərində qurmaq idi, lakin Gödelin natamamlıq teoreminə görə, hər bir (kifayət qədər güclü) aksiomatik sistemin həll olunmayan düsturları var; və buna görə də riyaziyyatın son aksiomatizasiyası mümkün deyil. Buna baxmayaraq, riyaziyyat çox vaxt (formal məzmununa görə) bəzi aksiomatizasiyada çoxluq nəzəriyyəsindən başqa bir şey deyil, o mənada təsəvvür edilir ki, hər bir riyazi ifadə və ya isbat çoxluqlar nəzəriyyəsi daxilində düsturlara çevrilə bilər.

Riyaziyyat mükafatları

Filds medalının ön tərəfi

Şübhəsiz ki, riyaziyyat üzrə ən prestijli mükafat 1936-cı ildə təsis edilən və dörd ildən bir (İkinci Dünya Müharibəsi istisna olmaqla) dörd nəfərə verilən Filds medalıdır.

1978-ci ildə təsis edilmiş riyaziyyat üzrə , digər böyük beynəlxalq mükafat, Abel mükafatı 2002-ci ildə təsis edilmiş və ilk dəfə 2003-cü ildə verilmişdir. Çern medalı nailiyyətləri qiymətləndirmək üçün 2010-cu ildə təqdim edilmişdir. Bu mükafatlar mühüm yeniliklər və ya hər hansı bir sahədəki görkəmli problemin həllinə görə verilir.

"Hilbert problemləri" adlanan 23 açıq problemdən ibarət məşhur siyahı 1900-cü ildə alman riyaziyyatçısı David Hilbert tərəfindən tərtib edilmişdir. İndi bu problemlərdən ən azı on üçü həll olunub. 2000-ci ildə "Minilliyin problemləri" adlanan yeddi mühüm problemdən ibarət yeni siyahı dərc olundu. Onlardan yalnız biri, Riman hipotezi Hilbertin problemlərindən birini təkrarlayır. Bu problemlərdən hər hansı birinin həllinə görə 1 milyon dollar mükafat verilir.

Hal-hazırda bu problemlərdən yalnız biri, Puankare hipotezi rus riyaziyyatçısı Qriqori Perelman tərəfindən həll edilmişdir. 2006-cı ildə Science jurnalı Perelmanın Puankare hipotezini isbat etməsini ilin elmi sıçrayışı kimi qeyd etmişdir.

Qeydlər

1. Evklidin sağlığındakı fiziki görünüşünə aid heç bir rəsm və ya təsvir antik dövrdən bu günümüzə qədər gəlib çatmamışdır. Buna görə də Evklidin sənət əsərlərindəki təsviri rəssamın təxəyyülündən asılıdır (bax: Evklid).
2. Buraya dairəvi silindrlər və müstəvilərlə kəsişmələri olan konus hissələr daxildir.
3. Fizika, kompüter elmi və digər riyazi elmlər kimi statistika da tətbiqi riyaziyyatın bir qolu olmaqdan əlavə, həm də müstəqil bir sahədir. Tədqiqatçı-fiziklər və kompüter alimləri kimi tədqiqatçı-statistiklər də riyaziyyatçı-alimlərdir. Bir çox statistikin riyaziyyat üzrə dərəcəsi var və bəzi statistiklər də riyaziyyatçıdır.
4. Formal isbatda səhv ola biləcək sadə nümunələr üçün yanlış isbata baxın.
5. İsbatda baş verən böyük hesablamanın etibarlı hesab edilməsi üçün, ümumiyyətlə, müstəqil proqram təminatından istifadə etməklə iki hesablama tələb olunur.
6. Tam isbatı ehtiva edən kitab 1000-dən çox səhifədən ibarətdir.

İstinadlar

1. "mathematics, n 2019-11-16 at the Wayback Machine.". Oxford English Dictionary. Oxford University Press. 2012. Archived from the original on November 16, 2019. Retrieved June 16, 2012. "The science of space, number, quantity, and arrangement, whose methods involve logical reasoning and usually the use of symbolic notation, and which includes geometry, arithmetic, algebra, and analysis".
2. Kneebone, G. T. (1963). Mathematical Logic and the Foundations of Mathematics: An Introductory Survey 2017-01-07 at the Wayback Machine. Dover. p. 4. . "Mathematics … is simply the study of abstract structures, or formal patterns of connectedness".
3. LaTorre, Donald R.; Kenelly, John W.; Biggers, Sherry S.; Carpenter, Laurel R.; Reed, Iris B.; Harris, Cynthia R. (2011). Calculus Concepts: An Informal Approach to the Mathematics of Change 2017-01-07 at the Wayback Machine. Cengage Learning. p. 2. . "Calculus is the study of change—how things change, and how quickly they change".
4. Ramana (2007). Applied Mathematics 2022-07-12 at the Wayback Machine. Tata McGraw–Hill Education. p. 2.10. . "The mathematical study of change, motion, growth or decay is calculus".
5. Ziegler, Günter M. (2011). "What Is Mathematics?" 2017-01-07 at the Wayback Machine. An Invitation to Mathematics: From Competitions to Research. Springer. p. vii. .
6. Mura, Roberta (December 1993). "Images of Mathematics Held by University Teachers of Mathematical Sciences". Educational Studies in Mathematics. 25 (4): 375–85. doi:10.1007/BF01273907. JSTOR 3482762 2022-07-12 at the Wayback Machine. S2CID 122351146.
7. Tobies, Renate & Helmut Neunzert (2012). Iris Runge: A Life at the Crossroads of Mathematics, Science, and Industry 2017-01-07 at the Wayback Machine. Springer. p. 9. . [I]t is first necessary to ask what is meant by mathematics in general. Illustrious scholars have debated this matter until they were blue in the face, and yet no consensus has been reached about whether mathematics is a natural science, a branch of the humanities, or an art form.
8. Peterson 2001, p. 12
9. Wigner, Eugene (1960). "The Unreasonable Effectiveness of Mathematics in the Natural Sciences". Communications on Pure and Applied Mathematics. 13 (1): 1–14. Bibcode:1960CPAM…13….1W. doi:10.1002/cpa.3160130102. 28 fevral 2011 tarixində arxivləşdirilib.
10. Wise, David. "Eudoxus' Influence on Euclid's Elements with a close look at The Method of Exhaustion" 2019-06-01 at the Wayback Machine. jwilson.coe.uga.edu. 1 iyun 2019 tarixində arxivləşdirilib 1.06.2019.
11. Luke Howard Hodgkin & Luke Hodgkin, A History of Mathematics, Oxford University Press, 2005.
12. Halpern, Joseph; Harper, Robert; Immerman, Neil; Kolaitis, Phokion; Vardi, Moshe; Vianu, Victor (2001). "On the Unusual Effectiveness of Logic in Computer Science" 2021-03-03 at the Wayback Machine (PDF).
13. Rao, C. R. (1997) Statistics and Truth: Putting Chance to Work, World Scientific.
14. Rao, C. R. (1981). "Foreword". In Arthanari, T. S.; Dodge, Yadolah (eds.). Mathematical programming in statistics. Wiley Series in Probability and Mathematical Statistics. New York: Wiley. pp. vii–viii. . MR 0607328.
15. Whittle (1994, pp. 10–11, 14–18): Whittle, Peter (1994). "Almost home". In Kelly, F. P. (ed.). Probability, statistics and optimisation: A Tribute to Peter Whittle (previously "A realised path: The Cambridge Statistical Laboratory up to 1993 (revised 2002)" ed.). Chichester: John Wiley. pp. 1–28. . 19 dekabr 2013 tarixində arxivləşdirilib.
16. Dehaene, Stanislas; Dehaene-Lambertz, Ghislaine; Cohen, Laurent (August 1998). "Abstract representations of numbers in the animal and human brain". Trends in Neurosciences. 21 (8): 355–61. doi:10.1016/S0166–2236(98)01263–6. PMID 9720604. S2CID 17414557.
17. See, for example, Raymond L. Wilder, Evolution of Mathematical Concepts; an Elementary Study, passim
18. Zaslavsky, Claudia. (1999). Africa Counts: Number and Pattern in African Culture 2021-03-31 at the Wayback Machine. Chicago Review Press. . OCLC 843204342. 31 mart 2021 tarixində arxivləşdirilib
19. Kline 1990, Chapter 1.
20. Boyer 1991, "Mesopotamia" pp. 24–27.
21. Heath, Thomas Little (1981) [1921]. A History of Greek Mathematics: From Thales to Euclid. New York: Dover Publications. p. 1. .
22. Boyer 1991, "Archimedes of Syracuse" p. 120.
23. Boyer 1991, "Archimedes of Syracuse" p. 130.
24. Boyer 1991, "Apollonius of Perga" p. 145
25. Boyer 1991, "Greek Trigonometry and Mensuration" p. 162.
26. Boyer 1991, "Revival and Decline of Greek Mathematics" p. 180.
27. Saliba, George. (1994). A history of Arabic astronomy: planetary theories during the golden age of Islam 2021-03-31 at the Wayback Machine. New York University Press. . OCLC 28723059. 31 mart 2021 tarixində arxivləşdirilib.
28. Sevryuk 2006, pp. 101–09
29. "mathematic (n.)". Online Etymology Dictionary.7 mart 2013 tarixində arxivləşdirilib
30. Both meanings can be found in Plato, the narrower in Republic 510c 24 fevral 2021 tarixində Wayback Machine tərəfindən arxivləşdirilib, lakin Platon riyaziyyat sözündən istifadə etməmişdir; Aristotel bunu şərh etdi. μαθηματική. Liddell, Henry George; Scott, Robert; A Greek–English Lexicon at the Perseus Project. OED Online, "Mathematics".
31. Boas, Ralph (1995) [1991]. "What Augustine Didn't Say About Mathematicians". Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories by the Late Ralph P. Boas, Jr. Cambridge University Press. p. 257. . 20 may 2020 tarixində arxivləşdirilib
32. The Oxford Dictionary of English Etymology, Oxford English Dictionary, sub "mathematics", "mathematic", "mathematics"
33. "maths, n." and "math, n.3" 2020-04-04 at the Wayback Machine 4 aprel 2020-ci ildə Wayback Machine-də arxivləşdirilib. Oxford English Dictionary, on-line version (2012).
34. Franklin, James (July 8, 2009). Philosophy of Mathematics. pp. 104–106. . 6 sentyabr 2015 tarixində arxivləşdirilib.
35. Cajori, Florian (1893). A History of Mathematics. American Mathematical Society (1991 reprint). pp. 285–86 2017-01-07 at the Wayback Machine.
36. Snapper, Ernst (September 1979). "The Three Crises in Mathematics: Logicism, Intuitionism, and Formalism". Mathematics Magazine. 52 (4): 207–16. doi:10.2307/2689412. JSTOR 2689412.
37. Peirce, Benjamin (1882). Linear Associative Algebra. Van Nostrand. p. 1.
38. Russell, Bertrand (1903). The Principles of Mathematics. p. 5. Retrieved June 20, 2015.
39. Iemhoff, Rosalie (March 4, 2020). Zalta, Edward N. (ed.). Intuitionism in the Philosophy of Mathematics. Metaphysics Research Lab, Stanford University. 31 mart 2021 tarixində arxivləşdirilib – via Stanford Encyclopedia of Philosophy.
40. Haskell Brooks Curry (1951). Outlines of a Formalist Philosophy of Mathematics 2017-01-07 at the Wayback Machine. Elsevier. p. 56. . Aç, səhifə 56 2022-03-21 at the Wayback Machine
41. Waltershausen 1965, p. 79.
42. du Sautoy, Marcus (June 25, 2010). "Nicolas Bourbaki". A Brief History of Mathematics. Event occurs at min. 12:50. BBC Radio 4. 16 dekabr 2016 tarixində arxivləşdirilib.
43. Popper, Karl (2002) 1959. The Logic of Scientific Discovery. Abingdon-on-Thames: Routledge. p. [18]. .
44. Bishop, Alan (1991). "Environmental activities and mathematical culture". Mathematical Enculturation: A Cultural Perspective on Mathematics Education. Norwell, Massachusetts: Kluwer Academic Publishers. pp. 20–59. . 25 dekabr 2020 tarixində arxivləşdirilib.
45. Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. p. 228.
46. Nickles, Thomas (2013). "The Problem of Demarcation". Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. Chicago: The University of Chicago Press. p. 104.
47. Pigliucci, Massimo (2014). "Are There 'Other' Ways of Knowing?". Philosophy Now. 13 may 2020 tarixində arxivləşdirilib.
48. See, for example Bertrand Russell's statement "Mathematics, rightly viewed, possesses not only truth, but supreme beauty …" in his History of Western Philosophy
49. "The science checklist applied: Mathematics". undsci.berkeley.edu. 27 oktyabr 2019 tarixində arxivləşdirilib.
50. Borel, Armand (March 2017). "Mathematics: Art and Science". EMS Newsletter. 3 (103): 37–45. doi:10.4171/news/103/8. ISSN 1027–488X.
51. Meinhard E. Mayer (2001). "The Feynman Integral and Feynman's Operational Calculus". Physics Today. 54 (8): 48. Bibcode:2001PhT….54h..48J 2021-09-27 at the Wayback Machine. doi:10.1063/1.1404851.
52. Steiner, Mark (1998). The Applicability of Mathematics as a Philosophical Problem. Cambridge, Mass: Harvard University Press. p. 176. ISBN .
53. Leng, Mary (2010). Mathematics and Reality. Oxford University Press. p. 239. ISBN .
54. "Mathematics Subject Classification 2010" (PDF). 14 may 2011 tarixində orijinalından (PDF).
55. Hardy, G. H. (1940). A Mathematician's Apology. Cambridge University Press. ISBN .
56. Gold, Bonnie; Simons, Rogers A. (2008). Proof and Other Dilemmas: Mathematics and Philosophy. MAA.
57. "Earliest Uses of Various Mathematical Symbols". 20 fevral 2016 tarixində arxivləşdirilib.
58. Kline 1990, p. 140, on Diophantus; p. 261, on Vieta.
59. Oakley 2014, p. 16: "Focused problem solving in math and science is often more effortful than focused-mode thinking involving language and people. This may be because humans haven't evolved over the millennia to manipulate mathematical ideas, which are frequently more abstractly encrypted than those of conventional language."
60. Oakley 2014, p. 16: "What do I mean by abstractness? You can point to a real live cow chewing its cud in a pasture and equate it with the letters c–o–w on the page. But you can't point to a real live plus sign that the symbol '+' is modeled after – the idea underlying the plus sign is more abstract."
61. Oakley 2014, p. 16: "By encryptedness, I mean that one symbol can stand for a number of different operations or ideas, just as the multiplication sign symbolizes repeated addition."
62. Ivars Peterson, The Mathematical Tourist, Freeman, 1988, . p. 4 "A few complain that the computer program can't be verified properly", (in reference to the Haken–Apple proof of the Four Color Theorem).
63. "The method of 'postulating' what we want has many advantages; they are the same as the advantages of theft over honest toil." Bertrand Russell (1919), Introduction to Mathematical Philosophy, New York and London, p. 71. 20 iyun 2015 tarixində Wayback Machine-də arxivləşdirilib.
64. Patrick Suppes, Axiomatic Set Theory, Dover, 1972, ISBN . p. 1, "Among the many branches of modern mathematics set theory occupies a unique place: with a few rare exceptions the entities which are studied and analyzed in mathematics may be regarded as certain particular sets or classes of objects."
65. Monastyrsky 2001, p. 1: "The Fields Medal is now indisputably the best known and most influential award in mathematics."
66. Riehm 2002, pp. 778–82
67. "The Wolf Prize". Wolf Foundation. 12 yanvar 2020 tarixində arxivləşdirilib.
68. "About the Abel Prize | The Abel Prize" 2022-04-14 at the Wayback Machine. abelprize.no.
69. "Abel Prize | mathematics award | Britannica" 2020-01-26 at the Wayback Machine. www.britannica.com.
70. "Chern Medal Award | International Mathematical Union (IMU)" 2010-08-25 at the Wayback Machine. www.mathunion.org.
71. "Hilbert's Problems: 23 and Math" 2022-01-23 at the Wayback Machine. Simons Foundation. may 6, 2020.
72. "The Millennium Prize Problems | Clay Mathematics Institute" 2015-07-03 at the Wayback Machine. www.claymath.org.
73. "Millennium Problems | Clay Mathematics Institute" 2018-12-20 at the Wayback Machine. www.claymath.org.
74. (Press-reliz). Clay Mathematics Institute. March 18, 2010. March 22, 2010 tarixində orijinalından (PDF) arxivləşdirilib. İstifadə tarixi: November 13, 2015. The Clay Mathematics Institute (CMI) announces today that Dr. Grigoriy Perelman of St. Petersburg, Russia, is the recipient of the Millennium Prize for resolution of the Poincaré conjecture.

Ədəbiyyat siyahısı

• Boyer, C. B. (1991). A History of Mathematics (2nd ed.). New York: Wiley. ISBN .
• Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN .
• Kline, Morris (1990). Mathematical Thought from Ancient to Modern Times (Paperback ed.). New York: Oxford University Press. ISBN .
• Monastyrsky, Michael (2001). "Some Trends in Modern Mathematics and the Fields Medal" (PDF). CMS – NOTES – de la SMC. Canadian Mathematical Society. 33 (2–3). 13 avqust 2006 tarixində orijinalından (PDF).
• Oakley, Barbara (2014). A Mind For Numbers: How to Excel at Math and Science (Even If You Flunked Algebra). New York: Penguin Random House. ISBN . A Mind for Numbers.
• Peirce, Benjamin (1881). Peirce, Charles Sanders (ed.). "Linear associative algebra". American Journal of Mathematics (Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed.). 4 (1–4): 97–229. doi:10.2307/2369153. hdl:2027/hvd.32044030622997. JSTOR 2369153. Corrected, expanded, and annotated revision with an 1875 paper by B. Peirce and annotations by his son, C. S. Peirce, of the 1872 lithograph ed. Google Eprint and as an extract, D. Van Nostrand, 1882, Google Eprint. 31 mart 2021 tarixində orijinalından .
• Peterson, Ivars (2001). Mathematical Tourist, New and Updated Snapshots of Modern Mathematics. Owl Books. ISBN .
• Popper, Karl R. (1995). "On knowledge". In Search of a Better World: Lectures and Essays from Thirty Years. New York: Routledge. Bibcode:1992sbwl.book….. P. ISBN .
• Riehm, Carl (August 2002). "The Early History of the Fields Medal" (PDF). Notices of the AMS. 49 (7): 778–82. 26 oktyabr 2006 tarixində orijinalından (PDF).
• Sevryuk, Mikhail B. (January 2006). "Book Reviews" (PDF). Bulletin of the American Mathematical Society. 43 (1): 101–09. doi:10.1090/S0273-0979-05-01069-4. 23 iyul 2006 tarixində orijinalından (PDF).
• Waltershausen, Wolfgang Sartorius von (1965) [first published 1856]. Gauss zum Gedächtniss. Sändig Reprint Verlag H. R. Wohlwend. ISBN .

Əlavə oxu üçün

• Benson, Donald C. (2000). The Moment of Proof: Mathematical Epiphanies. Oxford University Press. ISBN .
• Davis, Philip J.; Hersh, Reuben (1999). The Mathematical Experience (Reprint ed.). Mariner Books. ISBN .
• Courant, Richard; Robbins, Herbert (1996). What Is Mathematics?: An Elementary Approach to Ideas and Methods (2nd ed.). New York: Oxford University Press. ISBN .
• Einstein, Albert (1923). Sidelights on Relativity: I. Ether and relativity. II. Geometry and experience (translated by G. B. Jeffery, D. Sc., and W. Perrett, Ph. D). E. P. Dutton & Co., New York. Archived from the original on July 25, 2014. Retrieved September 23, 2012.
• Gullberg, Jan (1997). Mathematics: From the Birth of Numbers (1st ed.). W. W. Norton & Company. ISBN 978-0-393-04002-9.
• Hazewinkel, Michiel, ed. (2000). Encyclopaedia of Mathematics. Kluwer Academic Publishers. – Sovet riyaziyyat ensiklopediyasının tərcümə edilmiş və genişləndirilmiş versiyası, on cilddə. Həm də kağız nüsxədə və CD-ROM-da və onlayn 3 iyul 2011 tarixində Wayback Machine tərəfindən .
• Jourdain, Philip E. B. (2003). "The Nature of Mathematics". In James R. Newman (ed.). The World of Mathematics. Dover Publications. ISBN .
• Maier, Annaliese (1982). Steven Sargent (ed.). At the Threshold of Exact Science: Selected Writings of Annaliese Maier on Late Medieval Natural Philosophy. Philadelphia: University of Pennsylvania Press.
• Pappas, Theoni (June 1989). The Joy Of Mathematics (Revised ed.). Wide World Publishing. ISBN .