Hidroaeromexanika — axıcı maddələrin (mayelərin, qazların və plazmaların) mexanikasını və onlara təsir edən qüvvələri öyrənən fizika sahəsi. Onun mexaniki, mülki, kimyəvi və biotibbi mühəndislik, geofizika, okeanoqrafiya, meteorologiya, astrofizika və biologiya da daxil olmaqla geniş spektrdə tətbiqləri var.
Onu maye və qazların statikasına, yəni sükunətdə olan axıcıların öyrənilməsinə və onların dinamikasına, yəni qüvvələrin axıcıların hərəkətinə təsirinin öyrənilməsinə ayırmaq olar. O maddənin atomlardan təşkil olunduğunu nəzərə almadan onu modelləşdirən bütöv mühit mexanikasının bir qoludur; yəni burada maddə mikroskopik yox, makroskopik baxımdan modelləşdirilir. Hidroaeromexanika, xüsusən də hidroaerodinamika tipik olaraq kompleks riyazi aktiv tədqiqat sahəsidir. Bir çox problemlər qismən və ya tamamilə həll edilməmişdir və ən yaxşı formada isə ədədi üsullarla, adətən, kompüterlərdən istifadə etməklə həll edilmişdir. Hesablamalı hidroaerodinamika adlanan müasir elm sahəsi bu yanaşmaya həsr edilmişdir. Axınların vizuallaşdırılması və analizi üçün eksperimental üsul olan hissəciklərin sürətinin vizual ölçülməsi də axının yüksək vizual təbiətinə əsaslanır.
Qısa tarix
Hidroaeromexanikaya dair çalışmalar öz başlanğıcını ən azı Antik Yunanıstandan götürür. Bu dövrün ən sanballı çalışması Arximed tərəfindən maye və qazların statikasına və qaldırma qüvvəsinin tədqiqinə həsr olunmuş "Üzən Cisimlərə Dair" əsəridir. Hidroaeromexanikadakı böyük irəliləyişlər Leonardo da Vinçi (müşahidə və təcrübələr), Evangelista Toriçelli (barometrin icadı), İsaak Nyuton (özlülüyün tədqiqi), Blez Paskal (hidrostatikanın tədqiqi, Paskal qanunu) ilə başladı və Daniel Bernulli tərəfindən Hidrodinamika (1739) əsərində maye və qazların riyazi dinamikasının tanıdılması ilə davam etdi.
Sonralar qeyri-özlülüklü axının analizi müxtəlif riyaziyyatçılar (Jan Leron D'Alamber, Jozef Lui Laqranj, Pyer Simon Laplas, Simeon Denis Puasson) tərəfindən aparıldı, həmçinin və də daxil olmaqla bir çox mühəndislər tərəfindən tədqiq edildi. Klod Luis Navye və Corc Qabriel Stoks tərəfindən əlavə riyazi əsaslandırma Navye-Stoks tənliklərilə verildi və sərhəd təbəqələri araşdırıldı (, ), eyni zamanda Osborn Reynolds, Andrey Kolmoqorov və kimi alimlər maye və qazların özlülük və turbulentlik anlayışlarını inkişaf etdirdi.
Başlıca qolları
Hidroaerostatika
Axıcıların statikası və ya hidrostatika hidroaeromexanikanın tarazlıqda olan mayeləri öyrənən bölməsidir. O, stabil tarazlıqdakı axıcıların sükunət şərtlərinin öyrənilməsini əhatə edir və hərəkətdə olan axıcıların öyrənilməsi ilə məşğul olan hidroaerodinamika ilə ziddiyyət təşkil edir. Hidrostatika gündəlik həyatdakı bir çox hadisələrin, məsələn, atmosfer təzyiqinin nə üçün hündürlüyə görə dəyişdiyinin, odunun və yağın suda niyə üzdüyünün, sükunət halındakı su səthinin niyə düz olduğunun fiziki izahını verir. Hidrostatika hidravlika, yəni mayelərin saxlanması, daşınması və istifadəsiylə məşğul olan qurğular mühəndisliyi üçün əsasdır. O, həmçinin geofizika və astrofizikanın bəzi aspektlərinə (məsələn, litosfer lövhələrinin tektonikasının və Yerin qravitasiya sahəsindəki anomaliyaların öyrənilməsində), meteorologiyaya, tibbə (qan təzyiqi kontekstində) və bir çox başqa sahələrə daxildir.
Hidroaerodinamika
Hidroaerodinamika hidroaeromexanikanın altsahəsidir—maye və qazların hərəkəti haqqında elmdir. Hidroaerodinamika, axının ölçülməsindən alınan və praktik məsələləri həll etməyə yarayan empirik və yarı empirik qanunları əhatə edən—bu praktik fənlərin əsasında duran—sistematik bir struktur təqdim edir. Hidroaerodinamika məsələlərinin həllinə, adətən, sürət, təzyiq, sıxlıq və temperatur kimi müxtəlif xüsusiyyətlərin fəza və zamanın funksiyaları şəklində hesablanması daxildir. Bu elmin aerodinamika (havanın və digər qazların hərəkətini öyrənir) və hidrodinamika (mayelərin hərəkətini öyrənir) da daxil olmaqla bir çox alt sahəsi var. Hidroaerodinamika təyyarələrə təsir edən qüvvələrin və onların hərəkətlərinin hesablanması, boru kəmərləri vasitəsilə neftin kütləvi axınının təyin edilməsi, inkişaf edən hava nümunələrinin proqnozlaşdırılması, ulduzlararası fəzada dumanlıqların anlaşılması və partlayışların modelləşdirilməsi də daxil olmaqla çox müxtəlif tətbiq sahələrinə malikdir. Hidroaerodinamikanın bəzi prinsiplərindən nəqliyyat mühəndisliyində və xaos dinamikasında istifadə olunur.
Bütöv mühit mexanikasıyla əlaqəsi
Hidroaeromexanika, aşağıdakı cədvəldə göstərildiyi kimi, bütöv mühit mexanikasının alt sahələrindən biridir:
| Bütöv mühit mexanikası Bütöv (kəsilməz) materialların fizikasını öyrənən elm | Müəyyən olunmuş dayanıqlı formaya malik bütöv materialların fizikasını öyrənən elm. | Elastiklik Tətbiq olunmuş gərginliklər götürüldükdən sonra materialın dayanıqlı vəziyyətinə qayıtmasını təsvir edir. | |
| Plastiklik Kifayət həddə qüvvə tətbiq edildikdə qalıq deformasiyaya uğrayan materialları təsvir edir. | Reologiya Bərk və maye xüsusiyyətinə malik materialları öyrənən elm . | ||
Qüvvə tətbiq olunduqda formasını dəyişən bütöv materialların fizikasını öyrənən elm. | tətbiq olunmuş kəsici gərginliyə mütənasib olaraq nisbi deformasiya tezliyinə məruz qalmır. | ||
| tətbiq olunmuş kəsici gərginliyə mütənasib olaraq nisbi deformasiya tezliyinə məruz qalır. | |||
Mexanik görünüşə görə maye kəsmə gərginliyini dəstəkləməyən bir maddədir; buna görə də sükunət halında olan maye öz qabının formasına malikdir. Sükunət halındakı mayenin kəsmə gərginliyi yoxdur.
Fərziyyələr

Fiziki sistemin hidroaeromexaniki davranışına xas olan fərziyyələr riyazi tənliklərlə ifadə etmək olar. Prinsipcə, hər bir hidroaeromexaniki sistemin aşağıdakılara tabe olduğu fərz edilir:
- Enerjinin saxlanması
- Kəsilməzlik fərziyyəsi
Məsələn, kütlənin qorunub saxlanması fərziyyəsi o deməkdir ki, hər hansı sabit kontrol həcmi (məsələn, sferik həcm) üçün - kontrol səthiylə əhatə olunmuş - həmin həcmdə olan kütlənin dəyişmə sürəti kütlənin sürətinə bərabərdir. Kütlənin içəridən xaricə keçmə sürəti çıxılmaqla səthdən xaricdən içəriyə keçir. Bu, baxılan həcm üzrə inteqral formada tənlik kimi ifadə edilə bilər.
Kəsilməzlik fərziyyəsi mayelərin mikroskopik miqyasda molekullardan ibarət olsalar belə, özlərini kəsilməz kimi apardığı bütöv mühit mexanikasının ideallaşdırılmasıdır. Kəsilməzlik fərziyyəsinə əsasən, sıxlıq, təzyiq, temperatur və kütlə sürəti kimi makroskopik (müşahidə olunan/ölçülə bilən) xassələrin “sonsuz kiçik” həcm elementlərində yaxşı müəyyən edilməsi qəbul edilir – sistemin xarakterik uzunluq şkalası ilə müqayisədə kiçik, lakin molekulyar uzunluq şkalası ilə müqayisədə böyükdür. Mayenin xassələri bir həcm elementindən digərinə davamlı olaraq dəyişə bilər və molekulyar xassələrin orta qiymətləridir. Kəsilməzlik fərziyyəsi səsdən sürətli axınlar və ya nanomiqyasda molekulyar axınlar kimi tətbiqlərdə qeyri-dəqiq nəticələrə gətirib çıxara bilər. Kəsilməzlik fərziyyəsinin uğursuz olduğu problemlər statistik mexanikadan istifadə etməklə həll edilə bilər. Kəsilməzlik fərziyyəsinin tətbiq edilib-edilmədiyini müəyyən etmək üçün molekulyar orta sərbəst yolun xarakterik uzunluq ölçüsünə nisbəti kimi təyin olunan Knudsen ədədinin qiyməti hesablanır. 0.1-dən aşağı Knudsen ədədləri ilə bağlı problemlər kəsilməzlik hipotezindən istifadə etməklə qiymətləndirilə bilər, lakin daha böyük Knudsen ədədlərinə uyğun gələn mayenin hərəkətini tapmaq üçün molekulyar yanaşma (statistik mexanika) tətbiq oluna bilər.
Navye-Stoks tənlikləri
Navye-Stoks tənlikləri (Klod Luis Navye və Corc Qabriel Stoksun adını daşıyır) mayenin müəyyən nöqtəsində qüvvə balansını təsvir edən diferensial tənliklərdir. Vektori sürət sahəsi 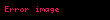
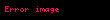
Bu diferensial tənliklər Nyutonun hissəcikləri üçün hərəkət tənliklərinin deformasiya olunan materialların analoqlarıdır–Navye-Stoks tənlikləri burada 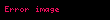
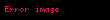
Verilmiş fiziki problem üçün Navye-Stoks tənliklərinin həlli variasiya hesabının köməyi ilə axtarılmalıdır. Praktik baxımdan yalnız ən sadə halları məhz bu şəkildə həll etmək olar. Bu hallar ümumiyyətlə Reynolds ədədinin kiçik olduğu qeyri-turbulent, kəsilməz axını əhatə edir. Daha mürəkkəb hallar üçün, xüsusən qlobal hava sistemləri, aerodinamika, hidrodinamika və daha çox kimi turbulentliklə bağlı hallar üçün Navye-Stoks tənliklərinin həlli hazırda yalnız kompüterlərin köməyi ilə tapıla bilər. Elmin bu sahəsi hesablamalı hidroaerodinamika adlanır.
Qeyri-özlülüklü və özlülüklü axıcılar
Qeyri-özlülüklü mayelərin özlülüyü sıfıra bərabərdir, 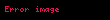
Məsaməli sərhəddən maye axını üçün mayenin sürəti sərbəst maye ilə məsaməli mühitdəki maye arasında fasiləsiz ola bilər (bu Beaver və Cozef vəziyyəti ilə bağlıdır). Bundan əlavə, aşağı səssiz sürətlərdə qazın sıxılmadığını düşünmək faydalıdır - yəni sürət və statik təzyiq dəyişsə də qazın sıxlığı dəyişmir.
Nyuton mayelərinə qarşı qeyri-Nyuton mayeləri
Nyuton mayesi (İsaak Nyutonun adını daşıyır) kəsmə gərginliyi kəsilmə müstəvisinə perpendikulyar istiqamətdə sürət qradiyenti ilə xətti mütənasib olan maye kimi müəyyən edilir. Bu tərif mayeyə təsir edən qüvvələrdən asılı olmayaraq onun axmağa davam etməsi deməkdir. Məsələn, su Nyuton mayesidir, çünki nə qədər qarışdırılsa da maye xüsusiyyətlərini göstərməyə davam edir. Bir az daha az ciddi bir tərif, mayenin içindən yavaş-yavaş hərəkət edən kiçik bir cismin sürüklənməsinin cismə tətbiq olunan qüvvə ilə mütənasib olmasıdır. (Sürtünmə ilə müqayisə edin). Su və qazların əksəriyyəti kimi mühüm mayelər Yerdə normal şəraitdə Nyuton mayesi kimi davranırlar.
Bunun əksinə olaraq, qeyri-Nyuton mayesinin qarışdırılması arxada "çuxur" buraxa bilər. Bu, zamanla tədricən dolacaq - bu davranış pudinq, ooblek və ya qum kimi materiallarda görünür (baxmayaraq ki, qum ciddi şəkildə maye deyil). Alternativ olaraq, qeyri-Newtonian mayenin qarışdırılması özlülüyün azalmasına səbəb ola bilər, buna görə də maye "nazik" görünür (bu, damcı olmayan boyalarda görünür). Qeyri-Nyuton mayelərinin bir çox növləri var, çünki onlar müəyyən bir xüsusiyyətə tabe olmayan bir şey kimi müəyyən edilir - məsələn, uzun molekulyar zəncirləri olan mayelərin əksəriyyəti Nyutondan fərqli bir şəkildə reaksiya verə bilər.
Nyuton mayesi üçün tənliklər
Özlülüklü gərginlik tenzoru ilə sürət qradiyenti arasındakı mütənasiblik sabiti özlülük adlanır. Sıxılmayan Nyuton mayesinin davranışını təsvir etmək üçün sadə bir tənlikdir.

burada


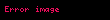
Nyuton mayesi üçün özlülük, tərifə görə, ona təsir edən qüvvələrdən deyil, yalnız temperatur və təzyiqdən asılıdır. Maye sıxılmayandırsa, özlü gərginliyin əsas tənliyi (Dekart koordinatlarında) belə yazılar:
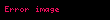


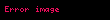
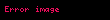
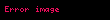
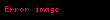

Maye sıxılmaz deyilsə, Nyuton mayesində özlü gərginliyin ümumi forması belədir
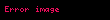
burada 

İstinadlar
- White, Frank M. (2011). Fluid Mechanics (7th ed.). McGraw-Hill. ISBN .
- Tu, Jiyuan; Yeoh, Guan Heng; Liu, Chaoqun (Nov 21, 2012). Computational Fluid Dynamics: A Practical Approach. ISBN .
- Batchelor, C. K., & Batchelor, G. K. (2000). An introduction to fluid dynamics. Cambridge University Press.
- Bertin, J. J., & Smith, M. L. (1998). Aerodynamics for engineers (Vol. 5). Upper Saddle River, NJ: Prentice Hall.
- Anderson Jr, J. D. (2010). Fundamentals of aerodynamics. Tata McGraw-Hill Education.
- Houghton, E. L., & Carpenter, P. W. (2003). Aerodynamics for engineering students. Elsevier.
- Milne-Thomson, L. M. (1973). Theoretical aerodynamics. Courier Corporation.
- Milne-Thomson, L. M. (1996). Theoretical hydrodynamics. Courier Corporation.
- Birkhoff, G. (2015). Hydrodynamics. Princeton University Press.
- Batchelor, George K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. p. 74. ISBN .
- Greenkorn, Robert (3 October 2018). Momentum, Heat, and Mass Transfer Fundamentals 2022-04-20 at the Wayback Machine. CRC Press. p. 18. ISBN .
- Constantin, P., & Foias, C. (1988). Navier-stokes equations. University of Chicago Press.
- Temam, R. (2001). Navier-Stokes equations: theory and numerical analysis (Vol. 343). American Mathematical Society.
- Foias, C., Manley, O., Rosa, R., & Temam, R. (2001). Navier-Stokes equations and turbulence (Vol. 83). Cambridge University Press.
- Girault, V., & Raviart, P. A. (2012). Finite element methods for Navier-Stokes equations: theory and algorithms (Vol. 5). Springer Science & Business Media.
- Anderson, J. D., & Wendt, J. (1995). Computational fluid dynamics (Vol. 206). New York: McGraw-Hill.
- Chung, T. J. (2010). Computational fluid dynamics. Cambridge University Press.
- Blazek, J. (2015). Computational fluid dynamics: principles and applications. Butterworth-Heinemann.
- Wesseling, P. (2009). Principles of computational fluid dynamics (Vol. 29). Springer Science & Business Media.
- Anderson, D., Tannehill, J. C., & Pletcher, R. H. (2016). Computational fluid mechanics and heat transfer. Taylor & Francis.
- Kundu, Pijush K.; Cohen, Ira M.; Dowling, David R. (27 March 2015). "10". Fluid Mechanics (6th ed.). Academic Press. ISBN .
Əlavə oxu üçün
- Falkovich, Gregory (2011), Fluid Mechanics (A short course for physicists), Cambridge University Press, doi:10.1017/CBO9780511794353,
- Kundu, Pijush K.; Cohen, Ira M. (2008), Fluid Mechanics (4th revised ed.), Academic Press,
- Currie, I. G. (1974), Fundamental Mechanics of Fluids, McGraw-Hill, Inc.,
- Massey, B.; Ward-Smith, J. (2005), Mechanics of Fluids (8th ed.), Taylor & Francis,
- Nazarenko, Sergey (2014), Fluid Dynamics via Examples and Solutions, CRC Press (Taylor & Francis group),
Xarici keçidlər
- Free Fluid Mechanics books
- Annual Review of Fluid Mechanics
- CFDWiki – Hesablamalı Hidroaerodinamika üçün vikiistinad.
- Educational Particle Image Velocimetry – resources and demonstrations
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Hidroaeromexanika axici maddelerin mayelerin qazlarin ve plazmalarin mexanikasini ve onlara tesir eden quvveleri oyrenen fizika sahesi Onun mexaniki mulki kimyevi ve biotibbi muhendislik geofizika okeanoqrafiya meteorologiya astrofizika ve biologiya da daxil olmaqla genis spektrde tetbiqleri var Onu maye ve qazlarin statikasina yeni sukunetde olan axicilarin oyrenilmesine ve onlarin dinamikasina yeni quvvelerin axicilarin hereketine tesirinin oyrenilmesine ayirmaq olar O maddenin atomlardan teskil olundugunu nezere almadan onu modellesdiren butov muhit mexanikasinin bir qoludur yeni burada madde mikroskopik yox makroskopik baximdan modellesdirilir Hidroaeromexanika xususen de hidroaerodinamika tipik olaraq kompleks riyazi aktiv tedqiqat sahesidir Bir cox problemler qismen ve ya tamamile hell edilmemisdir ve en yaxsi formada ise ededi usullarla adeten komputerlerden istifade etmekle hell edilmisdir Hesablamali hidroaerodinamika adlanan muasir elm sahesi bu yanasmaya hesr edilmisdir Axinlarin vizuallasdirilmasi ve analizi ucun eksperimental usul olan hisseciklerin suretinin vizual olculmesi de axinin yuksek vizual tebietine esaslanir Qisa tarixHidroaeromexanikaya dair calismalar oz baslangicini en azi Antik Yunanistandan goturur Bu dovrun en sanballi calismasi Arximed terefinden maye ve qazlarin statikasina ve qaldirma quvvesinin tedqiqine hesr olunmus Uzen Cisimlere Dair eseridir Hidroaeromexanikadaki boyuk irelileyisler Leonardo da Vinci musahide ve tecrubeler Evangelista Toricelli barometrin icadi Isaak Nyuton ozluluyun tedqiqi Blez Paskal hidrostatikanin tedqiqi Paskal qanunu ile basladi ve Daniel Bernulli terefinden Hidrodinamika 1739 eserinde maye ve qazlarin riyazi dinamikasinin tanidilmasi ile davam etdi Sonralar qeyri ozluluklu axinin analizi muxtelif riyaziyyatcilar Jan Leron D Alamber Jozef Lui Laqranj Pyer Simon Laplas Simeon Denis Puasson terefinden aparildi hemcinin ve de daxil olmaqla bir cox muhendisler terefinden tedqiq edildi Klod Luis Navye ve Corc Qabriel Stoks terefinden elave riyazi esaslandirma Navye Stoks tenliklerile verildi ve serhed tebeqeleri arasdirildi eyni zamanda Osborn Reynolds Andrey Kolmoqorov ve kimi alimler maye ve qazlarin ozluluk ve turbulentlik anlayislarini inkisaf etdirdi Baslica qollariHidroaerostatika Axicilarin statikasi ve ya hidrostatika hidroaeromexanikanin tarazliqda olan mayeleri oyrenen bolmesidir O stabil tarazliqdaki axicilarin sukunet sertlerinin oyrenilmesini ehate edir ve hereketde olan axicilarin oyrenilmesi ile mesgul olan hidroaerodinamika ile ziddiyyet teskil edir Hidrostatika gundelik heyatdaki bir cox hadiselerin meselen atmosfer tezyiqinin ne ucun hundurluye gore deyisdiyinin odunun ve yagin suda niye uzduyunun sukunet halindaki su sethinin niye duz oldugunun fiziki izahini verir Hidrostatika hidravlika yeni mayelerin saxlanmasi dasinmasi ve istifadesiyle mesgul olan qurgular muhendisliyi ucun esasdir O hemcinin geofizika ve astrofizikanin bezi aspektlerine meselen litosfer lovhelerinin tektonikasinin ve Yerin qravitasiya sahesindeki anomaliyalarin oyrenilmesinde meteorologiyaya tibbe qan tezyiqi kontekstinde ve bir cox basqa sahelere daxildir Hidroaerodinamika Hidroaerodinamika hidroaeromexanikanin altsahesidir maye ve qazlarin hereketi haqqinda elmdir Hidroaerodinamika axinin olculmesinden alinan ve praktik meseleleri hell etmeye yarayan empirik ve yari empirik qanunlari ehate eden bu praktik fenlerin esasinda duran sistematik bir struktur teqdim edir Hidroaerodinamika meselelerinin helline adeten suret tezyiq sixliq ve temperatur kimi muxtelif xususiyyetlerin feza ve zamanin funksiyalari seklinde hesablanmasi daxildir Bu elmin aerodinamika havanin ve diger qazlarin hereketini oyrenir ve hidrodinamika mayelerin hereketini oyrenir da daxil olmaqla bir cox alt sahesi var Hidroaerodinamika teyyarelere tesir eden quvvelerin ve onlarin hereketlerinin hesablanmasi boru kemerleri vasitesile neftin kutlevi axininin teyin edilmesi inkisaf eden hava numunelerinin proqnozlasdirilmasi ulduzlararasi fezada dumanliqlarin anlasilmasi ve partlayislarin modellesdirilmesi de daxil olmaqla cox muxtelif tetbiq sahelerine malikdir Hidroaerodinamikanin bezi prinsiplerinden neqliyyat muhendisliyinde ve xaos dinamikasinda istifade olunur Butov muhit mexanikasiyla elaqesiHidroaeromexanika asagidaki cedvelde gosterildiyi kimi butov muhit mexanikasinin alt sahelerinden biridir Butov muhit mexanikasi Butov kesilmez materiallarin fizikasini oyrenen elm Mueyyen olunmus dayaniqli formaya malik butov materiallarin fizikasini oyrenen elm Elastiklik Tetbiq olunmus gerginlikler goturuldukden sonra materialin dayaniqli veziyyetine qayitmasini tesvir edir Plastiklik Kifayet hedde quvve tetbiq edildikde qaliq deformasiyaya ugrayan materiallari tesvir edir Reologiya Berk ve maye xususiyyetine malik materiallari oyrenen elm Quvve tetbiq olunduqda formasini deyisen butov materiallarin fizikasini oyrenen elm tetbiq olunmus kesici gerginliye mutenasib olaraq nisbi deformasiya tezliyine meruz qalmir tetbiq olunmus kesici gerginliye mutenasib olaraq nisbi deformasiya tezliyine meruz qalir Mexanik gorunuse gore maye kesme gerginliyini desteklemeyen bir maddedir buna gore de sukunet halinda olan maye oz qabinin formasina malikdir Sukunet halindaki mayenin kesme gerginliyi yoxdur FerziyyelerKontrol sethi ile ehate olunmus kontrol hecminde bezi inteqrasiya olunmus maye miqdari ucun balans Fiziki sistemin hidroaeromexaniki davranisina xas olan ferziyyeler riyazi tenliklerle ifade etmek olar Prinsipce her bir hidroaeromexaniki sistemin asagidakilara tabe oldugu ferz edilir Enerjinin saxlanmasi Kesilmezlik ferziyyesi Meselen kutlenin qorunub saxlanmasi ferziyyesi o demekdir ki her hansi sabit kontrol hecmi meselen sferik hecm ucun kontrol sethiyle ehate olunmus hemin hecmde olan kutlenin deyisme sureti kutlenin suretine beraberdir Kutlenin iceriden xarice kecme sureti cixilmaqla sethden xaricden iceriye kecir Bu baxilan hecm uzre inteqral formada tenlik kimi ifade edile biler Kesilmezlik ferziyyesi mayelerin mikroskopik miqyasda molekullardan ibaret olsalar bele ozlerini kesilmez kimi apardigi butov muhit mexanikasinin ideallasdirilmasidir Kesilmezlik ferziyyesine esasen sixliq tezyiq temperatur ve kutle sureti kimi makroskopik musahide olunan olcule bilen xasselerin sonsuz kicik hecm elementlerinde yaxsi mueyyen edilmesi qebul edilir sistemin xarakterik uzunluq skalasi ile muqayisede kicik lakin molekulyar uzunluq skalasi ile muqayisede boyukdur Mayenin xasseleri bir hecm elementinden digerine davamli olaraq deyise biler ve molekulyar xasselerin orta qiymetleridir Kesilmezlik ferziyyesi sesden suretli axinlar ve ya nanomiqyasda molekulyar axinlar kimi tetbiqlerde qeyri deqiq neticelere getirib cixara biler Kesilmezlik ferziyyesinin ugursuz oldugu problemler statistik mexanikadan istifade etmekle hell edile biler Kesilmezlik ferziyyesinin tetbiq edilib edilmediyini mueyyen etmek ucun molekulyar orta serbest yolun xarakterik uzunluq olcusune nisbeti kimi teyin olunan Knudsen ededinin qiymeti hesablanir 0 1 den asagi Knudsen ededleri ile bagli problemler kesilmezlik hipotezinden istifade etmekle qiymetlendirile biler lakin daha boyuk Knudsen ededlerine uygun gelen mayenin hereketini tapmaq ucun molekulyar yanasma statistik mexanika tetbiq oluna biler Navye Stoks tenlikleriNavye Stoks tenlikleri Klod Luis Navye ve Corc Qabriel Stoksun adini dasiyir mayenin mueyyen noqtesinde quvve balansini tesvir eden diferensial tenliklerdir Vektori suret sahesi u displaystyle mathbf u olan sixilmayan maye ucun Navye Stoks tenlikleri asagidaki kimidir u t u u 1r P n 2u displaystyle displaystyle frac partial mathbf u partial t mathbf u cdot nabla mathbf u frac 1 rho nabla P nu nabla 2 mathbf u Bu diferensial tenlikler Nyutonun hissecikleri ucun hereket tenliklerinin deformasiya olunan materiallarin analoqlaridir Navye Stoks tenlikleri burada n displaystyle nu kinematik ozluluyu ile parametrlesdirilmis P displaystyle P tezyiqine ve ozluluyune cavab olaraq impulsda quvvede deyisiklikleri tesvir edir Bezen tenliklere qravitasiya quvvesi ve ya Lorens quvvesi kimi cisim quvveleri de elave olunur Verilmis fiziki problem ucun Navye Stoks tenliklerinin helli variasiya hesabinin komeyi ile axtarilmalidir Praktik baximdan yalniz en sade hallari mehz bu sekilde hell etmek olar Bu hallar umumiyyetle Reynolds ededinin kicik oldugu qeyri turbulent kesilmez axini ehate edir Daha murekkeb hallar ucun xususen qlobal hava sistemleri aerodinamika hidrodinamika ve daha cox kimi turbulentlikle bagli hallar ucun Navye Stoks tenliklerinin helli hazirda yalniz komputerlerin komeyi ile tapila biler Elmin bu sahesi hesablamali hidroaerodinamika adlanir Qeyri ozluluklu ve ozluluklu axicilarQeyri ozluluklu mayelerin ozluluyu sifira beraberdir n 0 displaystyle nu 0 Praktikada ozluluksuz axin riyazi emeliyyatlari sadelesdirmek ucun istifade olunan idellasdirmadir Eslinde sirf ozluluksuz axinlarin yalniz ifrataxiciliq veziyyetinde gerceklesdiyi melumdur Eks teqdirde mayeler umumiyyetle ozludur bu xususiyyet berk sethe yaxin olan serhed tebeqesi yaxinliginda cox vaxt muhumdur burada axin berk cismin surusmemesi veziyyetine uygun olmalidir Bezi hallarda mayenin mexaniki sisteminin riyazi hesablamalarini serhed tebeqelerinden kenarda olan mayenin qeyri sabit oldugunu qebul ederek ve sonra onun hellini nazik laminar serhed tebeqesi ucun uygunlasdirmaqla yerine yetirmek olar Mesameli serhedden maye axini ucun mayenin sureti serbest maye ile mesameli muhitdeki maye arasinda fasilesiz ola biler bu Beaver ve Cozef veziyyeti ile baglidir Bundan elave asagi sessiz suretlerde qazin sixilmadigini dusunmek faydalidir yeni suret ve statik tezyiq deyisse de qazin sixligi deyismir Nyuton mayelerine qarsi qeyri Nyuton mayeleriNyuton mayesi Isaak Nyutonun adini dasiyir kesme gerginliyi kesilme mustevisine perpendikulyar istiqametde suret qradiyenti ile xetti mutenasib olan maye kimi mueyyen edilir Bu terif mayeye tesir eden quvvelerden asili olmayaraq onun axmaga davam etmesi demekdir Meselen su Nyuton mayesidir cunki ne qeder qarisdirilsa da maye xususiyyetlerini gostermeye davam edir Bir az daha az ciddi bir terif mayenin icinden yavas yavas hereket eden kicik bir cismin suruklenmesinin cisme tetbiq olunan quvve ile mutenasib olmasidir Surtunme ile muqayise edin Su ve qazlarin ekseriyyeti kimi muhum mayeler Yerde normal seraitde Nyuton mayesi kimi davranirlar Bunun eksine olaraq qeyri Nyuton mayesinin qarisdirilmasi arxada cuxur buraxa biler Bu zamanla tedricen dolacaq bu davranis pudinq ooblek ve ya qum kimi materiallarda gorunur baxmayaraq ki qum ciddi sekilde maye deyil Alternativ olaraq qeyri Newtonian mayenin qarisdirilmasi ozluluyun azalmasina sebeb ola biler buna gore de maye nazik gorunur bu damci olmayan boyalarda gorunur Qeyri Nyuton mayelerinin bir cox novleri var cunki onlar mueyyen bir xususiyyete tabe olmayan bir sey kimi mueyyen edilir meselen uzun molekulyar zencirleri olan mayelerin ekseriyyeti Nyutondan ferqli bir sekilde reaksiya vere biler Nyuton mayesi ucun tenlikler Ozluluklu gerginlik tenzoru ile suret qradiyenti arasindaki mutenasiblik sabiti ozluluk adlanir Sixilmayan Nyuton mayesinin davranisini tesvir etmek ucun sade bir tenlikdir t mdvdy displaystyle tau mu dv over dy burada t displaystyle tau axici terefinden tetbiq olunan kesme gerginliyi m displaystyle mu mutenasiblik emsali olub maye ve qazin ozluluyu adlanir dvdy displaystyle dv over dy ise surusme istiqametine perpendikulyar olan suret qradiyentidir Nyuton mayesi ucun ozluluk terife gore ona tesir eden quvvelerden deyil yalniz temperatur ve tezyiqden asilidir Maye sixilmayandirsa ozlu gerginliyin esas tenliyi Dekart koordinatlarinda bele yazilar tij m vi xj vj xi m ivj displaystyle displaystyle tau ij mu left frac partial v i partial x j frac partial v j partial x i right mu partial i v j tij displaystyle tau ij j displaystyle j ci istiqametde maye ve ya qaz elementinin i displaystyle i ci uzunun kesilme gerginliyi vi displaystyle v i i displaystyle i ci istiqametindeki suret xj displaystyle x j j displaystyle j ci istiqametin koordinatidir Maye sixilmaz deyilse Nyuton mayesinde ozlu gerginliyin umumi formasi beledir tij m vi xj vj xi 23dij v kdij v displaystyle displaystyle tau ij mu left frac partial v i partial x j frac partial v j partial x i frac 2 3 delta ij nabla cdot mathbf v right kappa delta ij nabla cdot mathbf v burada k displaystyle kappa ikinci ozluluk emsalidir ve ya hecmi ozlulukdur Eger maye bu elaqeye tabe olmursa o bir nece novu olan qeyri Nyuton mayesi adlanir Qeyri Nyuton mayeleri plastik Binqham plastik psevdoplastik dilatant tiksotrop reopektik viskoelastik ola biler Bezi tetbiqlerde mayeler arasinda qaba sekilde basqa bir genis bolgu aparilir ideal ve qeyri ideal axicilar Ideal maye ozlu deyil ve kesme quvvesine hec bir muqavimet gostermir Ideal maye heqiqeten movcud deyil lakin bezi hesablamalarda ferziyye kimi esaslandirilir Buna misal olaraq berk sethlerden uzaq olan axini gostermek olar Bir cox hallarda ozlu tesirler berk serhedlerin yaxinliginda cemlesir meselen serhed tebeqelerinde axin sahesinin serhedlerden uzaq bolgelerinde ise ozlu tesirlere laqeyd yanasmaq ve oradaki mayenin ozlu olmadigini ideal axin qebul etmek olar Ozluluk nezere alinmadiqda Navye Stoks tenliyinde ozluluklu gerginlik tenzoru t displaystyle tau ehtiva eden hedd yox olur Bu formada sadelesdirilen tenliye Eyler tenliyi deyilir IstinadlarWhite Frank M 2011 Fluid Mechanics 7th ed McGraw Hill ISBN 978 0 07 352934 9 Tu Jiyuan Yeoh Guan Heng Liu Chaoqun Nov 21 2012 Computational Fluid Dynamics A Practical Approach ISBN 978 0080982434 Batchelor C K amp Batchelor G K 2000 An introduction to fluid dynamics Cambridge University Press Bertin J J amp Smith M L 1998 Aerodynamics for engineers Vol 5 Upper Saddle River NJ Prentice Hall Anderson Jr J D 2010 Fundamentals of aerodynamics Tata McGraw Hill Education Houghton E L amp Carpenter P W 2003 Aerodynamics for engineering students Elsevier Milne Thomson L M 1973 Theoretical aerodynamics Courier Corporation Milne Thomson L M 1996 Theoretical hydrodynamics Courier Corporation Birkhoff G 2015 Hydrodynamics Princeton University Press Batchelor George K 1967 An Introduction to Fluid Dynamics Cambridge University Press p 74 ISBN 0 521 66396 2 Greenkorn Robert 3 October 2018 Momentum Heat and Mass Transfer Fundamentals 2022 04 20 at the Wayback Machine CRC Press p 18 ISBN 978 1 4822 9297 8 Constantin P amp Foias C 1988 Navier stokes equations University of Chicago Press Temam R 2001 Navier Stokes equations theory and numerical analysis Vol 343 American Mathematical Society Foias C Manley O Rosa R amp Temam R 2001 Navier Stokes equations and turbulence Vol 83 Cambridge University Press Girault V amp Raviart P A 2012 Finite element methods for Navier Stokes equations theory and algorithms Vol 5 Springer Science amp Business Media Anderson J D amp Wendt J 1995 Computational fluid dynamics Vol 206 New York McGraw Hill Chung T J 2010 Computational fluid dynamics Cambridge University Press Blazek J 2015 Computational fluid dynamics principles and applications Butterworth Heinemann Wesseling P 2009 Principles of computational fluid dynamics Vol 29 Springer Science amp Business Media Anderson D Tannehill J C amp Pletcher R H 2016 Computational fluid mechanics and heat transfer Taylor amp Francis Kundu Pijush K Cohen Ira M Dowling David R 27 March 2015 10 Fluid Mechanics 6th ed Academic Press ISBN 978 0124059351 Elave oxu ucunFalkovich Gregory 2011 Fluid Mechanics A short course for physicists Cambridge University Press doi 10 1017 CBO9780511794353 ISBN 978 1 107 00575 4 Kundu Pijush K Cohen Ira M 2008 Fluid Mechanics 4th revised ed Academic Press ISBN 978 0 12 373735 9 Currie I G 1974 Fundamental Mechanics of Fluids McGraw Hill Inc ISBN 0 07 015000 1 Massey B Ward Smith J 2005 Mechanics of Fluids 8th ed Taylor amp Francis ISBN 978 0 415 36206 1 Nazarenko Sergey 2014 Fluid Dynamics via Examples and Solutions CRC Press Taylor amp Francis group ISBN 978 1 43 988882 7Xarici kecidlerFree Fluid Mechanics books Annual Review of Fluid Mechanics CFDWiki Hesablamali Hidroaerodinamika ucun vikiistinad Educational Particle Image Velocimetry resources and demonstrations
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans