Lambda hesablaması

Lambda hesablanması (λ-hesablama) — hesablama anlayışını formalaşdırmaq və təhlil etmək üçün Amerika riyaziyyatçısı Alonzo Çörç tərəfindən hazırlanmış rəsmi bir sistem.

Saf ${\displaystyle \lambda }$- hesablama

Saf ${\displaystyle \lambda }$- hesablamasışərtləri həmçinin , obyektləri ("obami")və ya Lambda (hərf-λ) şərtləri adlanan tətbiq və abstraksiya istifadə edərək yalnız dəyişənlərdən qurulmuşdur. Əvvəlcə hər hansı bir sabitliyin olması ehtimal edilmir.

Tətbiq və abstraksiya

Əsasən λ-hesablama iki əsas əməliyyata əsaslanır:

• Tətbiq (lat. applicatio — qoşma, qoşulmaq) müəyyən bir dəyərlə əlaqədar bir funksiyanı tətbiq etmək və ya çağırmaq deməkdir. Adətən onun işarəsi${\displaystyle f\ a}$,hardaki, ${\displaystyle f\ a}$ — funksiya, a isə ${\displaystyle a}$ — arqumentdir.Bu riyaziyyatda ümumi olan ${\displaystyle f(a)}$ notasiyaya uyğun gəlir,bəzən də həmçinin də istifadə olunur,lakin, λ-hesablama üçün ${\displaystyle f}$-in nəticəni verilən giriş dəyərindən hesablayan alqoritm kimi qəbul etməsi vacibdir. Bu mənada ${\displaystyle f}$,${\displaystyle a}$ tətbiqinə iki cür baxmaq olar: tətbiqi nəticəsində ${\displaystyle f}$ -dan ${\displaystyle a}$ -ya və yaxudda hesablama prosesi olaraq ${\displaystyle f\ a}$. Tətbiqin son şərhi β-azalma anlayışı ilə əlaqədardır.
• Abstraksiya və ya λ-abstraksiya (lat. abstractio — yayındırma,bölmə) öz növbəsində verilmiş ifadələrə uyğun olaraq funksiyalar qurur. Eynilə,əgər ${\displaystyle t\equiv t[x]}$ — ifadəsi sərbəst olan ${\displaystyle x}$, onda qeyd ${\displaystyle \ \lambda x.t[x]}$ bu mənanı verir: ${\displaystyle \lambda }$ arqumentdən funksiyası ${\displaystyle x}$, formaya sahibdir ${\displaystyle t[x]}$,bir funksiyanı ifadə edir ${\displaystyle x\mapsto t[x]}$. Beləliklə, abstraksiya istifadə edərək yeni funksiyalar qura bilərsiniz. Tələb belə ki,${\displaystyle x}$ sərbəst şəkildə ${\displaystyle t}$ -ya,daxil edilirsə, çox əhəmiyyətli deyil — fərz etmək kifayətdir${\displaystyle \lambda x.t\equiv t}$,əgər bu belə deyilsə.

α-ekvivalentlik

Lambda baxımından müəyyən edilən ekvivalentliyin əsas forması alfa ekvivalentliyidir. Məsələn, ${\displaystyle \lambda x.x}$ və ${\displaystyle \lambda y.y}$ : alfa ekvivalent lambda şərtləri və hər ikisi eyni funksiyanı təmsil edir: alfa ekvivalent lambda terminləri və hər ikisi eyni funksiyanı təmsil edir. Lambda abstraksiyasında olmadığı üçün ${\displaystyle x}$ və ${\displaystyle y}$ şərtləri alfa ekvivalenti deyildir.

β-reduksiyası

${\displaystyle \lambda x.2\cdot x+1}$ ifadəsi bu funksiyanı ifadə edir,qəbulu hər birinə görə ${\displaystyle x}$ dəyəri ${\displaystyle 2\cdot x+1}$, sonra ifadəni hesablamaq üçün

${\displaystyle (\lambda x.2\cdot x+1)\ 3}$,

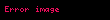
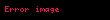
həm tətbiqi, ${\displaystyle x}$ dəyişən əvəzinə həm də mücərrədliyi ehtiva edən müddətdə 3 sayının dəyişdirilməsini yerinə ${\displaystyle 2\cdot x+1}$ yetirmək lazımdır. Nəticədə ${\displaystyle 2\cdot 3+1=7}$ alınır. Bu mülahizə ümumi şəkildə

${\displaystyle (\lambda x.t)\ a=t[x:=a],}$

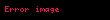
yazılır və β-azalma adlanır. İfadənin növü {\displaystyle (\lambda x.t)\ a}(\lambda x.t)\ a-ya, yəni müəyyən bir müddətə bir abstraksiya tətbiq etmək, redex adlanır (redex). Baxmayaraq ki,sonra, o β-azalma lambda — hesablanmasının əslində çox əsaslı və mürəkkəb bir nəzəriyyəyə səbəb olan yeganə "əsas" aksiomadır{\displaystyle \lambda }\. Onunla birlikdə ${\displaystyle \lambda }$- hesablaması Tyurinq tamlıq xüsusiyyətinə malikdir və buna görə də ən sadə proqramlaşdırma dilidir.

η-çevrilməsi

${\displaystyle \eta }$ — çevrilməsi iki funksiyanın eyni və yalnız olduqda eyni olduğunu düşüncəsini,nə zaman, hər hansı bir dəlil tətbiq olunanda eyni nəticələri ifadə edir. ${\displaystyle \eta }$- dönüşümü ${\displaystyle \lambda x.f\ x}$ и ${\displaystyle f}$ düsturlarını bir-birinə çevirir(əgər ki,${\displaystyle x}$-ın ${\displaystyle f}$-ya sərbəst girişi yoxdursa: əks halda sərbəst dəyişən ${\displaystyle x}$ çevrilmədən sonra əlaqəli xarici abstraksiya və ya əksinə olacaq).

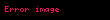
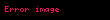
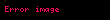
Əyrilmə(Kurrinq)

İki dəyişənin funksiyası ${\displaystyle x}$ и ${\displaystyle y}$ ${\displaystyle f(x,y)=x+y}$${\displaystyle x}$-ın bir dəyişənin funksiyası hesab edilə bilər, bir dəyişən funksiyasını qaytaran${\displaystyle y}$, yeni bir ifadə${\displaystyle \ \lambda x.\lambda y.x+y}$ olur. Bu texnika istənilən ariyanın funksiyaları üçün eyni şəkildə işləyir. Bu göstərir ki, bir çox dəyişənlərin funksiyaları ${\displaystyle \lambda }$— hesablaması ilə ifadə edilə bilər və "Sintaktik şəkər"dir. Bir çox dəyişkənliyin funksiyalarını bir dəyişənin funksiyasına çevirmək təsvir edilən proses, Amerika riyaziyyatçısı Haskell Kurrinin şərəfinə, karinq adlanır (M.E.Sheinfinkel (1924)).

Tipsiz hesablama ${\displaystyle \lambda }$-semantikası

Bu bir faktdır ki,${\displaystyle \lambda }$— lambda hesablamasının şərtləri funksiyaları kimi fəaliyyət göstərir,${\displaystyle \lambda }$— şərtlərə tətbiq olunur(bu bəlkə də,özü-özünə),${\displaystyle \lambda }$— hesablaması adekvat semantikanın qurulmasında çətinliklərə səbəb olur. ${\displaystyle \lambda }$— hesablanmasına hər hansı bir məna vermək üçün,${\displaystyle D}$ çoxluğunu almaq zəruridir,hansıki,onun funksional məkanına${\displaystyle D\to D}$ sərmayə qoyulacaqdı. Bunun ümumi vəziyyətində${\displaystyle D}$ ${\displaystyle D}$ və ${\displaystyle D}$-dan ${\displaystyle D}$-yə qədər funksiyalarbu iki çoxluğun gücünün məhdudlaşdırılması səbəbindən mövcud deyildir: ikincisi birincisindən daha çox gücə malikdir.

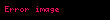
Bu çətinliyi 1970-ci illərin əvvəllərində Dana Skott aradan qaldırdı,${\displaystyle D}$ bir domen anlayışını quraraq (əvvəlcə tam rəflərdə,daha sonra tam bir qismən sifariş edilmiş xüsusi bir topologiya ilə ümumiləşdirərək) və kəsərək ${\displaystyle D\to D}$davamlı olaraq bu funksiyasını yaratdı. Bu konstruksiyaların əsasında,bunların köməyi ilə proqramlaşdırma dillərinin rekursion və məlumat növləri kimi iki vacib quruluşa dəqiq məna verə bilməsi üçün xüsusən proqramlaşdırma dillərinin ^[en] yaradıldı.

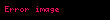
Rekursiv funksiyalarla əlaqə

Rekursiya — özü vasitəsilə bir funksiyanın tərifidir; ilk baxışdan lambda hesablaması buna imkan vermir,lakin bu təəssürat yanıldır. Məsələn, faktorial hesablayan bir rekursiv funksiyasını nəzərdən keçirək:

f(n) = 1, if n = 0; else n × f(n - 1).

Lambda hesablamasında bir funksiya birbaşa özünə edə bilməz. Bununla birlikdə, bir funksiya funksiyaya ötürülə bilər. Bir qayda olaraq, bu mübahisə əvvəlcə gəlir.Bir funksiya ilə əlaqələndirərək yeni, onsuz da təkrarlanan bir funksiya əldə edirik. Bunun üçün özünə istinad edən bir dəlil (burada 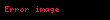${\displaystyle r}$ olaraq təyin olunur),funksiya orqanına ötürülməlidir.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Bu, faktorial hesablama problemini həll edir, lakin ümumi bir də mümkündür. Rekursiv bir funksiya və ya dövrü təmsil edən bir lambda müddəti alaraq, özünü ilk dəlil olaraq keçərək sabit nöqtəli kombinator lazımi rekursiv funksiyanı və ya dövrü geri qaytaracaqdır. Funksiyaların hər dəfə açıq şəkildə özlərini keçməsinə ehtiyac yoxdur.

Sabit nöqtəli kombinatorların bir neçə tərifi var. Onlardan ən sadəsi:

Y = λg.(λx.g (x x)) (λx.g (x x)) lambda hesablamasında, ${\displaystyle \operatorname {Y\ g} }$ — sabit nöqtə ${\displaystyle \operatorname {g} }$; bunu nümayiş etdirir:

Y g

(λh.(λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g). İndi faktorialı müəyyən etmək üçün, rekursiv funksiyası olaraq sadəcə yaza bilərik${\displaystyle \operatorname {g\ (Y\ g)} n}$,hardaki, ${\displaystyle n}$ — nömrə hansıki faktorialın hesablandlğı nömrədir. ${\displaystyle n=4}$ -dən,əldə edirik:

g (Y g) 4

 (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4 (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4 1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0 4·(g(Y g) 3) 4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3) 4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0) 4·(3·(g(Y g) 2)) 4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2)) 4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0)) 4·(3·(2·(g(Y g) 1))) 4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1))) 4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0))) 4·(3·(2·(1·((Y g) 0)))) 4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0)))) 4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0)))) 4·(3·(2·(1·(1)))) 24 

Bir rekursiv funksiyanın hər tərifi müvafiq funksiyanın sabit bir nöqtəsi kimi göstərilə bilər, buna görə də ${\displaystyle \operatorname {Y} }$ istufadə edilərək,hər rekursiv tərif lambda ifadəsi kimi ifadə edilə bilər. Xüsusilə, toplama işlənməsini, vurma, natural ədədlərin müqayisəsini rekursiv olaraq təyin edə bilərik.

Proqramlaşdırma dillərində

Proqramlaşdırma dillərində "${\displaystyle \lambda }$-hesablaması" tez-tez " anonim funksiyaların" mexanizmi başa düşülür — callback funksiyaları,hansı ki,istifadə edildikləri yerlərdə və cari funksiyanın (dəyişmə) lokal dəyişənlərinə giriş imkanı olan yerlərdə müəyyən edilə bilər.

İstinadlar

1. Scott D.S. The lattice of flow diagrams.-- Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.-- Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311–372.
2. Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

Ədəbiyyat

Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика. M.: Мир. 1985. səh. 606 .

Həmçinin bax

• Lambda-CDM model
• Standart Model
• Lambda-zond

Xarici keçidlər

• λ-Hesablama: Sonra & İndi (ing.)
• Lambda hesablaması (ing.)
• Lambda Hesablamasına qısa bir giriş (ing.)
• Lambda hesablaması — addımbaaddım (ing.)

Vikianbarda Lambda hesablaması ilə əlaqəli mediafayllar var.