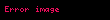Vektor (lat. vector — "daşıyıcı") — istiqamətlənmiş düz xətt parçası. Riyaziyyat, fizika və mühəndislikdə vektor dedikdə, Evklid fəzasında (və ya müstəvidə) ədədi qiyməti və istiqaməti ilə xarakterizə olunan həndəsi obyekt başa düşülür.

Vektorlara misal kimi radius vektoru, sürət və moment vektorlarını göstərmək olar. Əgər fəzada koordinat sistemi verilərsə, vektor onun koordinatlar çoxluğu ilə yeganə formada təyin oluna bilər. Buna görə də riyaziyyat, informatika və başqa elmlərdə nizamlı ədədlər çoxluğuna vektor deyilir. Daha ümumi mənada, riyaziyyatda vektor hər hansı vektor (xətti) fəzanın elementi kimi qəbul edilir.
Xətti cəbrdə vektorlar ümumi formada matris, tenzor kimi ifadə oluna bilir, bu halda vektor dedikdə müvafiq olaraq bir sıra və ya sütun vektoru, birinci tərtib tenzor kimi başa düşülür. Vektorlar üzərindəki əməllərin xassələri vektor hesabında öyrənilir.
Təyinatları

.
Kəmiyyətin vektor olduğunu vurğulamaq üçün yuxarı xətt və ya oxdan, qalın və ya qotik şriftdən istifadə edilir:
Vektorların toplanması demək olar ki, həmişə plyus işarəsiylə göstərilir:
.
Ədədə (skalyara) vurma xüsusi bir işarə olmadan sadəcə onun yanında yazıla bilər, məsələn:
,
ədəd isə həmişə solda yazılır. Bir matrisə vurma xüsusi bir işarə olmadan onun yanında yazmaqla da göstərilir, lakin burada ümumi vəziyyətdə amillərin permutasiyası nəticəyə təsir göstərir. Xətti bir operatorun bir vektorda hərəkəti, solda operatoru xüsusi işarə olmadan yazmaqla da göstərilir.
Tarixi
Intuitiv olaraq bir vektor, miqyası, istiqaməti və (istəyə bağlı) tətbiq nöqtəsi olan bir obyekt kimi başa düşülür. Vektor hesablamasının rudimentsləri kompleks ədədlərin həndəsi modeli ilə birlikdə ortaya çıxdı (Qauss, 1831). Uilyam Rouen Hamilton, işlənmiş əməliyyatları vektorlarla hesablamasının bir hissəsi olaraq yayımladı (dördüncü xəyali komponentlər vektoru meydana gətirdi). Uilyam Rouen Hamilton, vektor termini (lat. vector — "daşıyıcı") təklif etdi və vektor analizinin bəzi əməliyyatlarını təsvir etdi. Bu formalizm Ceyms Maksvell tərəfindən elektromaqnetizmə dair əsərlərində istifadə edilmiş və bununla da elm adamlarının diqqətini yeni hesablamaya cəlb etmişdir. Tezliklə Cozayya Uillard Gibbsin Vektor analizinin elementləri çıxdı (1880-ci illər), sonra Hevisayd Oliver (1903-cü il) vektor analizinə müasir bir görünüş verdi. Ümumiyyətlə qəbul edilmiş vektor işarələmələri yoxdur; qalın tip, hərfin üstündəki xətt və ya ox, qot əlifbası və s. istifadə olunur.
Həndəsədə
Həndəsədə vektorlar istiqamətlənmiş düz xətt parçaları deməkdir. Bu təfsir çox vaxt kompüter qrafiklərində, işıqlandırma xəritələrini qurmaqda, səthlərə normadan istifadə etməkdə istifadə olunur. Vektorlardan istifadə edərək üçbucaqlar və paraleloqramlar kimi müxtəlif formaların sahələrini, həm də cisimlərin həcmi: tetraedr və paralelepiped də tapa bilərsiniz. Bəzən bir istiqamət bir vektorla təyin olunur.
Həndəsədə bir vektor təbii olaraq bir köçürmə (paralel köçürmə) ilə əlaqələndirilir ki, bu da açıq şəkildə adının mənşəyini aydınlaşdırır(lat. vector, daşıyıcı). Həqiqətən, istənilən yönümlü düz xətt parçası müstəvi və ya fəzanın paralel ötürülməsini misilsiz şəkildə müəyyənləşdirir və əksinə, paralel ötürmə tək bir yönümlü parçanı müəyyənləşdirir (birmənalı şəkildə — eyni istiqamətdə və uzunluqdakı bütün yönümlü parçalar bərabər hesab olunursa — yəni onlar sərbəst vektorlar hesab olunur). Bir vektorun köçürmə kimi şərh edilməsi, əlavə vektorların işləməsini — iki (və ya bir neçə) köçürmənin tərkibi (ardıcıl istifadəsi) kimi təqdim etmək üçün təbii və intuitiv şəkildə açıq bir yol təqdim etməyə imkan verir; eyni, bir vektorun bir sıra ilə vurulması əməlinə aiddir.
Xətti cəbrdə
Xətti cəbrdə bir vektor aşağıda göstərilən ümumi tərifə uyğun bir xətti fəzanın elementidir. Vektorlar fərqli bir təbiətə sahib ola bilər: yönləndirilmiş parçalar, matrislər, ədədlər, funksiyalar və digərləri, eyni ölçülü bütün xətti fəzalar bir-birinə . Bir vektor anlayışı ən çox xətti cəbri tənliklər sistemlərinin həllində, habelə xətti operatorlarla işləyərkən istifadə olunur (xətti operatorun nümunəsi fırlanma operatorudur). Tez-tez bu tərif norma və ya skalyar bir məhsul (bəlkə də hər ikisi) müəyyənləşdirilərək genişlənir, bundan sonra onlar normallaşdırılmış və Evklid fəzalarında fəaliyyət göstərirlər, vektorlar arasındakı bucaq anlayışını skalyar məhsulu ilə və vektorun uzunluğu anlayışını norma ilə bağlayırlar. Bir çox riyazi obyektlər (məsələn, matrislər, tenzorlar və s.), o cümlədən sonlu (və bəzən hətta sayıla bilən) sifariş edilmiş siyahıdan daha ümumi bir quruluşa sahib olanlar, bir vektor fəzasının aksiomları, yəni cəbr baxımından, vektorlardır.
Funksional analizdə
Funksional analiz funksional fəzaları — sonsuz ölçülü nəzərdən keçirir. Onların elementləri funksiyalar ola bilər. Bir funksiyanın bu təqdimatına əsasən Furye sıraları nəzəriyyəsi qurulur. Eynilə, xətti cəbr ilə, bir norma, bir skalyar məhsul və ya bir funksiya sahəsindəki bir metrik tətbiq olunur.
Diferensial tənliklərin həlli üçün bəzi üsullar, məsələn, son element metodu, Hilbert fəzasının bir elementi kimi bir fəaliyyət anlayışına əsaslanır.
Ümumi tərif
Bir vektorun ən ümumi tərifi ümumi cəbr vasitəsi ilə verilir:
- Qeyd edək ki,
(qotik F) bir çox elementi olan bəzi sahə
, əlavə əməliyyat
,çoxaltma əməliyyatı
, və uyğun neytral elementlər: əlavə hissə
və multiplikativ vahid
ilə ifadə olur.
(qotik V)bəzi Abel qrupunu
elementlər dəsti ilə, əlavə işləmə
və müvafiq olaraq, aşqar birliyi
ilə ifadə edirik.
Başqa sözlə, 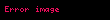
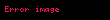
Bir əməliyyat varsa 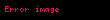
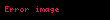
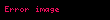
,
,
,
,
sonra
sahənin üstündən
vektor boşluğu adlanır (və ya xətti boşluq),
elementləri vektorlar adlanır,
elementləri — skalyarlar adlanır,
— göstərilən əməliyyat bir vektoru skalyara vurmadır.
Xətti cəbrin bir çox nəticəsi komutativ olmayan cisimlər və hətta ixtiyari modullar üzərində vahid modullara ümumiləşdirilir, buna görə də ən ümumi vəziyyətdə, bəzi kontekstlərdə bir üzük üzərində modulun istənilən elementinə vektor deyilə bilər.
Fiziki şərh
Həm qiyməti, həm də istiqməti olan struktur kimi vektor fizikada sürət, qüvvə və əlaqəli kəmiyyətlərin, kinematika və ya dinamikanın riyazi modeli kimi nəzərdən keçirilir. Bir çox fiziki sahələrin riyazi modeli (məsələn, elektromaqnit sahələri və ya maye sürət sahələri) vektor meydanlarıdır.
Abstrakt çoxölçülü və sonsuz ölçülü (funksional analiz ruhunda) vektor fəzaları Laqranj və Hamilton formalizmində mexaniki və digər dinamik sistemlərə tətbiq edildiyi kimi, kvant mexanikasında da tətbiq olunur.
Vektor ardıcıllıq kimi
Vektor — bircins elementlərdən ibarət dəstdir. Bu adi vektor əməllərinin ümumiyyətlə göstərilməməsi, daha az olması və ya xətti məkanın adi aksiomalarına cavab verə bilməməsi baxımından ən ümumi tərifdir. Bu formada vektorun proqramlaşdırmada başa düşüldüyü, burada, bir qayda olaraq, kvadrat mötərizədə (məsələn, obyekt []) olan identifikator adı ilə işarə olunur. Xassələrin siyahısı sistem nəzəriyyəsində qəbul edilən bir obyektin sinfini və vəziyyətini təyin edir. Beləliklə, vektor elementlərinin növləri cismin sinifini, elementlərin dəyərləri isə onun vəziyyətini müəyyənləşdirir. Ancaq, ehtimal ki, terminin bu cür istifadəsi cəbrdə və ümumiyyətlə riyaziyyatda ümumiyyətlə qəbul olunanlardan artıqdır.
Arifmetik vektor n ədədlərin yığılması əmrinə deyilir. Bu 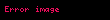
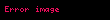

Həmçinin bax
İstinadlar
- Вектор // Математическая энциклопедия (в 5 томах) 2013-11-13 at the Wayback Machine. — М.: Советская Энциклопедия, 1977. — Т. 1.
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник (3-е изд). СПб.: ЛКИ. 2008. ISBN .
- Линейная алгебра. ИЭТ МЭИ Краткий конспект лекций http://old.exponenta.ru/educat/systemat/slivina/lection/lection3/lection3.asp 2019-11-26 at the Wayback Machine
Ədəbiyyat
- Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. М: Высшая школа. 1985. 232.
- J. V. Field. 'The Invention of Infinity: Mathematics and Art in the Renaissance. Oxford University Press. 1997. ISBN .
- J. Perez, Mécanique physique, Masson, 2007 ISBN
- M. B. Karbo, Le graphisme et l'internet, Compétence micro, № 26, 2002 ISBN
- F. Casiro, A. Deledicq, Pythagore et Thalès Les éditions du Kangourou 1998 ISBN
- R. Pouzergues, Les Hexamys, IREM de Nice, IremOuvrage, 1993 Cote : IM8974 Lire
- D. Lehmann et Rudolf Bkouche, Initiation à la géométrie, PUF, 1988, ISBN
- Y. Sortais, La Géométrie du triangle. Exercices résolus, Hermann, 1997, ISBN
- Y. Ladegaillerie, Géométrie pour le CAPES de mathématiques, Ellipses Marketing, 2002 ISBN
Xarici keçidlər
- Vektor anlayışı, vektorlar üzərində xətti əməllər (PDF)
- Vektor nədir?
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu adin diger istifade formalari ucun bax Vektor Vektor lat vector dasiyici istiqametlenmis duz xett parcasi Riyaziyyat fizika ve muhendislikde vektor dedikde Evklid fezasinda ve ya mustevide ededi qiymeti ve istiqameti ile xarakterize olunan hendesi obyekt basa dusulur AB displaystyle overrightarrow AB vektoru Vektorlara misal kimi radius vektoru suret ve moment vektorlarini gostermek olar Eger fezada koordinat sistemi verilerse vektor onun koordinatlar coxlugu ile yegane formada teyin oluna biler Buna gore de riyaziyyat informatika ve basqa elmlerde nizamli ededler coxluguna vektor deyilir Daha umumi menada riyaziyyatda vektor her hansi vektor xetti fezanin elementi kimi qebul edilir Xetti cebrde vektorlar umumi formada matris tenzor kimi ifade oluna bilir bu halda vektor dedikde muvafiq olaraq bir sira ve ya sutun vektoru birinci tertib tenzor kimi basa dusulur Vektorlar uzerindeki emellerin xasseleri vektor hesabinda oyrenilir Teyinatlaria1 a2 an displaystyle a 1 a 2 ldots a n elementlerinden komponentlerinden ibaret vektor asagidaki sekillerde isarelenir a1 a2 an a1 a2 an a1 a2 an displaystyle langle a 1 a 2 ldots a n rangle left a 1 a 2 ldots a n right a 1 a 2 ldots a n Kemiyyetin vektor oldugunu vurgulamaq ucun yuxari xett ve ya oxdan qalin ve ya qotik sriftden istifade edilir a a a A a displaystyle bar a vec a mathbf a mathfrak A mathfrak a Vektorlarin toplanmasi demek olar ki hemise plyus isaresiyle gosterilir a b displaystyle vec a vec b Edede skalyara vurma xususi bir isare olmadan sadece onun yaninda yazila biler meselen kb displaystyle k vec b eded ise hemise solda yazilir Bir matrise vurma xususi bir isare olmadan onun yaninda yazmaqla da gosterilir lakin burada umumi veziyyetde amillerin permutasiyasi neticeye tesir gosterir Xetti bir operatorun bir vektorda hereketi solda operatoru xususi isare olmadan yazmaqla da gosterilir TarixiIntuitiv olaraq bir vektor miqyasi istiqameti ve isteye bagli tetbiq noqtesi olan bir obyekt kimi basa dusulur Vektor hesablamasinin rudimentsleri kompleks ededlerin hendesi modeli ile birlikde ortaya cixdi Qauss 1831 Uilyam Rouen Hamilton islenmis emeliyyatlari vektorlarla hesablamasinin bir hissesi olaraq yayimladi dorduncu xeyali komponentler vektoru meydana getirdi Uilyam Rouen Hamilton vektor termini lat vector dasiyici teklif etdi ve vektor analizinin bezi emeliyyatlarini tesvir etdi Bu formalizm Ceyms Maksvell terefinden elektromaqnetizme dair eserlerinde istifade edilmis ve bununla da elm adamlarinin diqqetini yeni hesablamaya celb etmisdir Tezlikle Cozayya Uillard Gibbsin Vektor analizinin elementleri cixdi 1880 ci iller sonra Hevisayd Oliver 1903 cu il vektor analizine muasir bir gorunus verdi Umumiyyetle qebul edilmis vektor isarelemeleri yoxdur qalin tip herfin ustundeki xett ve ya ox qot elifbasi ve s istifade olunur HendesedeEsas meqale Vektor hendese Hendesede vektorlar istiqametlenmis duz xett parcalari demekdir Bu tefsir cox vaxt komputer qrafiklerinde isiqlandirma xeritelerini qurmaqda sethlere normadan istifade etmekde istifade olunur Vektorlardan istifade ederek ucbucaqlar ve paraleloqramlar kimi muxtelif formalarin sahelerini hem de cisimlerin hecmi tetraedr ve paralelepiped de tapa bilersiniz Bezen bir istiqamet bir vektorla teyin olunur Hendesede bir vektor tebii olaraq bir kocurme paralel kocurme ile elaqelendirilir ki bu da aciq sekilde adinin menseyini aydinlasdirir lat vector dasiyici Heqiqeten istenilen yonumlu duz xett parcasi mustevi ve ya fezanin paralel oturulmesini misilsiz sekilde mueyyenlesdirir ve eksine paralel oturme tek bir yonumlu parcani mueyyenlesdirir birmenali sekilde eyni istiqametde ve uzunluqdaki butun yonumlu parcalar beraber hesab olunursa yeni onlar serbest vektorlar hesab olunur Bir vektorun kocurme kimi serh edilmesi elave vektorlarin islemesini iki ve ya bir nece kocurmenin terkibi ardicil istifadesi kimi teqdim etmek ucun tebii ve intuitiv sekilde aciq bir yol teqdim etmeye imkan verir eyni bir vektorun bir sira ile vurulmasi emeline aiddir Xetti cebrdeXetti cebrde bir vektor asagida gosterilen umumi terife uygun bir xetti fezanin elementidir Vektorlar ferqli bir tebiete sahib ola biler yonlendirilmis parcalar matrisler ededler funksiyalar ve digerleri eyni olculu butun xetti fezalar bir birine Bir vektor anlayisi en cox xetti cebri tenlikler sistemlerinin hellinde habele xetti operatorlarla isleyerken istifade olunur xetti operatorun numunesi firlanma operatorudur Tez tez bu terif norma ve ya skalyar bir mehsul belke de her ikisi mueyyenlesdirilerek genislenir bundan sonra onlar normallasdirilmis ve Evklid fezalarinda fealiyyet gosterirler vektorlar arasindaki bucaq anlayisini skalyar mehsulu ile ve vektorun uzunlugu anlayisini norma ile baglayirlar Bir cox riyazi obyektler meselen matrisler tenzorlar ve s o cumleden sonlu ve bezen hetta sayila bilen sifaris edilmis siyahidan daha umumi bir qurulusa sahib olanlar bir vektor fezasinin aksiomlari yeni cebr baximindan vektorlardir Funksional analizdeFunksional analiz funksional fezalari sonsuz olculu nezerden kecirir Onlarin elementleri funksiyalar ola biler Bir funksiyanin bu teqdimatina esasen Furye siralari nezeriyyesi qurulur Eynile xetti cebr ile bir norma bir skalyar mehsul ve ya bir funksiya sahesindeki bir metrik tetbiq olunur Diferensial tenliklerin helli ucun bezi usullar meselen son element metodu Hilbert fezasinin bir elementi kimi bir fealiyyet anlayisina esaslanir Umumi terifBir vektorun en umumi terifi umumi cebr vasitesi ile verilir Qeyd edek ki F displaystyle mathfrak F qotik F bir cox elementi olan bezi sahe F displaystyle F elave emeliyyat displaystyle coxaltma emeliyyati displaystyle ve uygun neytral elementler elave hisse 0 displaystyle 0 ve multiplikativ vahid 1 displaystyle 1 ile ifade olur V displaystyle mathfrak V qotik V bezi Abel qrupunu V displaystyle V elementler desti ile elave isleme displaystyle ve muvafiq olaraq asqar birliyi 0 displaystyle mathbf 0 ile ifade edirik Basqa sozle F F displaystyle mathfrak F langle F rangle i V V displaystyle mathfrak V langle V rangle aliriq Bir emeliyyat varsa F V V displaystyle F times V to V her hansi biri ucun bele a b F displaystyle a b in F i dlya lyubyh x y V displaystyle mathbf x mathbf y in V nisbetler ifade olunur a b x a x b x displaystyle a b times mathbf x a times mathbf x b times mathbf x a x y a x a y displaystyle a times mathbf x mathbf y a times mathbf x a times mathbf y a b x a b x displaystyle a b times mathbf x a times b times mathbf x 1 x x displaystyle 1 times mathbf x mathbf x sonra F displaystyle mathfrak F sahenin ustunden V displaystyle mathfrak V vektor boslugu adlanir ve ya xetti bosluq V displaystyle V elementleri vektorlar adlanir F displaystyle F elementleri skalyarlar adlanir F V V displaystyle F times V to V gosterilen emeliyyat bir vektoru skalyara vurmadir Xetti cebrin bir cox neticesi komutativ olmayan cisimler ve hetta ixtiyari modullar uzerinde vahid modullara umumilesdirilir buna gore de en umumi veziyyetde bezi kontekstlerde bir uzuk uzerinde modulun istenilen elementine vektor deyile biler Fiziki serhHem qiymeti hem de istiqmeti olan struktur kimi vektor fizikada suret quvve ve elaqeli kemiyyetlerin kinematika ve ya dinamikanin riyazi modeli kimi nezerden kecirilir Bir cox fiziki sahelerin riyazi modeli meselen elektromaqnit saheleri ve ya maye suret saheleri vektor meydanlaridir Abstrakt coxolculu ve sonsuz olculu funksional analiz ruhunda vektor fezalari Laqranj ve Hamilton formalizminde mexaniki ve diger dinamik sistemlere tetbiq edildiyi kimi kvant mexanikasinda da tetbiq olunur Vektor ardicilliq kimiVektor bircins elementlerden ibaret destdir Bu adi vektor emellerinin umumiyyetle gosterilmemesi daha az olmasi ve ya xetti mekanin adi aksiomalarina cavab vere bilmemesi baximindan en umumi terifdir Bu formada vektorun proqramlasdirmada basa dusulduyu burada bir qayda olaraq kvadrat moterizede meselen obyekt olan identifikator adi ile isare olunur Xasselerin siyahisi sistem nezeriyyesinde qebul edilen bir obyektin sinfini ve veziyyetini teyin edir Belelikle vektor elementlerinin novleri cismin sinifini elementlerin deyerleri ise onun veziyyetini mueyyenlesdirir Ancaq ehtimal ki terminin bu cur istifadesi cebrde ve umumiyyetle riyaziyyatda umumiyyetle qebul olunanlardan artiqdir Arifmetik vektor n ededlerin yigilmasi emrine deyilir Bu x x1 x2 xn displaystyle overline x x 1 x 2 ldots x n isare edilmisdir x1 x2 xn displaystyle x 1 x 2 ldots x n bir arifmetik vektorun komponentleri adlanir Bir cox hesab vektoru hansi ki bunun ucun elave emeliyyatlar teyin olunur ve sayina gore coxalir arifmetik vektorlarin boslugu adlanirRn displaystyle R n Hemcinin baxVektor hendese Vektor Vektor displeyi Vektor prosessoruIstinadlarVektor Matematicheskaya enciklopediya v 5 tomah 2013 11 13 at the Wayback Machine M Sovetskaya Enciklopediya 1977 T 1 Aleksandrova N V Istoriya matematicheskih terminov ponyatij oboznachenij Slovar spravochnik 3 e izd SPb LKI 2008 ISBN 978 5 382 00839 4 Linejnaya algebra IET MEI Kratkij konspekt lekcij http old exponenta ru educat systemat slivina lection lection3 lection3 asp 2019 11 26 at the Wayback MachineEdebiyyatGusyatnikov P B Reznichenko S V Vektornaya algebra v primerah i zadachah M Vysshaya shkola 1985 232 J V Field The Invention of Infinity Mathematics and Art in the Renaissance Oxford University Press 1997 ISBN 0198523947 J Perez Mecanique physique Masson 2007 ISBN 2225553416 M B Karbo Le graphisme et l internet Competence micro 26 2002 ISBN 2912954959 F Casiro A Deledicq Pythagore et Thales Les editions du Kangourou 1998 ISBN 2 87694 040 X R Pouzergues Les Hexamys IREM de Nice IremOuvrage 1993 Cote IM8974 Lire D Lehmann et Rudolf Bkouche Initiation a la geometrie PUF 1988 ISBN 2130401600 Y Sortais La Geometrie du triangle Exercices resolus Hermann 1997 ISBN 270561429X Y Ladegaillerie Geometrie pour le CAPES de mathematiques Ellipses Marketing 2002 ISBN 2729811486Xarici kecidlerVikianbarda elaqeli media fayllar Vektor anlayisi vektorlar uzerinde xetti emeller PDF Vektor nedir
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans