Matris

Matris – düzbucaqlı sxemdə yerləşən a_ij elementləri (ədədlər, funksiyalar, üzərində cəbri əməllər aparıla bilən başqa kəmiyyətlər) sistemi. Onun m sətri və n sütunu varsa, deyilir ki, (m×n)–ölçülü matris verilmişdir. Məsələn,

m sətir və n sütundan ibarət m × n ölçülü matris. Matrisin hər bir elementi çox vaxt ikiqat aşağı indekslə işarələnir. Məsələn, a_2,1 matrisin ikinci sətir və birinci sütunundakı elementi göstərir.

${\displaystyle {\begin{bmatrix}1&9&-13\\20&5&-6\end{bmatrix}}}$

matrisi iki sətirə və üç sütuna malik 2×3 ölçülü matrisdir.

Matrislər əlavə spesifikasiyalar olmadan xətti çevirmələri təsvir edir və xətti cəbrdə aşkar hesablamalar aparmağa imkan verir. Buna görə də matrislərin tədqiqi xətti cəbrin böyük bir bölümünü təşkil edir və abstrakt xətti cəbrin əksər xassə və əməlləri matrislərlə ifadə oluna bilir. Məsələn, matrislərin hasili xətti çevirmələrin kompozisiyasını ifadə edir.

Matrislərin hamısı xətti cəbrlə əlaqəli deyil. Bu xüsusən qraf nəzəriyyəsində, insident və qonşuluq matrislərində belədir.

Bu məqalədə xətti cəbrlə əlaqəli matrislərə diqqət yetirilir və əgər digər hallar göstərilməyibsə, bütün matrislər xətti çevirmələri ifadə edir

Eyni sayda sətir və sütuna malik matrislər (kvadrat matrislər) matrislər nəzəriyyəsində böyük rol oynayır. Verilmiş ölçülü kvadrat matrislər qeyri-kommutativ halqa əmələ gətirir ki, bu da qeyri-kommutativ halqanın ən ümumi nümunələrindən biridir. Kvadrat matrisin determinantı kvadrat matrisin öyrənilməsi üçün əsas sayılan matrislə əlaqəli ədəddir; məsələn, kvadrat matris yalnız və yalnız sıfırdan fərqli determinanta malik olduqda və onun məxsusi qiymətləri çoxhədli determinantının kökləri olduqda tərs olur.

Həndəsədə matrislər həndəsi çevirmələri (məsələn, dönmələri) və koordinat dəyişmələrini təyin etmək və göstərmək üçün geniş istifadə olunur. Ədədi analizdəki bir çox hesablama məsələləri matris hesablamaya gətirilməklə həll edilir və bu, çox vaxt böyük ölçülü matrislərlə hesablamanı əhatə edir. Matrislər riyaziyyatın əksər sahələrində və bir çox elm sahələrində ya birbaşa, ya da həndəsə və ədədi analizdə istifadə yoluyla tətbiq olunur.

Tərif

Matris ədədlərin (və ya digər riyazi obyektlərin) düzbucaqlı yığımıdır. Matrisdəki ədəd, simvol və ya ifadələr onun ünsürləri və ya elementləri, ünsürlərdən ibarət üfüqi və şaquli sıralar isə müvafiq olaraq sətir və sütunlar adlanır.

Matrislər toplama və vurma kimi standart əməllərə tabedir. Ən geniş yayılmış F meydanı üzərindəki matris F elementlərinin düzbucaqlı yığımıdır.Ünsürləri uyğun olaraq həqiqi və ya kompleks ədədlər olan matris, həqiqi və ya kompleks matris adlanır.

Ölçü

Matrisin ölçüsü ona daxil olan sətir və sütunların sayı ilə xarakterizə olunur. Müsbət tam ədədlər olduqları müddətcə, bir matrisin (ümumi mənada) malik ola biləcəyi sətir və sütunların sayında heç bir məhdudiyyət yoxdur. m sətir və n sütundan ibarət matris m×n ölçülü matris və ya m-in n-ə matris adlanır. Məsələn, yuxarıdakı A matrisi 3×2 ölçülü matrisdir.

Yalnız bir sətirdən ibarət olan matris sətir vektoru, bir sütundan ibarət olan matris isə sütun vektoru adlanır. Eyni sayda sətir və sütuna malik olan matrisə kvadrat matris deyilir. Sonsuz sayda sətir və ya sütunu (və ya hər ikisi) olan matrisə sonsuz matris deyilir. Bəzi kontekstlərdə, məsələn, kompüter cəbri proqramlarında, sətirləri və ya sütunları olmayan, boş matrisi nəzərdən keçirmək faydalıdır.

Matris ölçüsünə ümumi baxış

Adı	Ölçüsü	Nümunə	Təsvir
Sətir vektoru	1 × n	${\displaystyle {\begin{bmatrix}3&7&2\end{bmatrix}}}$	Bir sətirli matris olub, bəzən vektoru göstərmək üçün istifadə edilir
Sütun vektoru	n × 1	${\displaystyle {\begin{bmatrix}4\\1\\8\end{bmatrix}}}$	Bir sütunlu matris olub, bəzən vektoru göstərmək üçün istifadə edilir
Kvadrat matris	n × n	${\displaystyle {\begin{bmatrix}9&13&5\\1&11&7\\2&6&3\end{bmatrix}}}$	Bərabər sayda sətir və sütuna malik matris, bəzən vektor fəzasından özünə xətti çevirməni (məsələn, əksetmə, dönmə və ya sürüşməni) göstərmək üçün istifadə olunur

İşarələmə

Matrislər, adətən, düzbucaqlı və ya dairəvi mötərizə daxilində yazılır:

${\displaystyle \mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}=\left(a_{ij}\right)\in \mathbb {R} ^{m\times n}.}$

Matrisin simvolik şəkildə göstərilmə xüsusiyyətləri bəzi yayğın meyllərlə birlikdə böyük ölçüdə dəyişir. Matrislər, adətən, böyük hərflərdən istifadə edilməklə (məsələn, yuxarıdakı nümunələrdə A kimi), buna uyğun olaraq ünsürlər isə iki işarəli aşağı indeksə malik kiçik hərflərlə (məsələn, a₁₁ və ya a_1,1) işarələnir. Bir çox müəlliflər matrisləri işarələmək üçün böyük hərflərdən istifadə etməklə yanaşı, matrisləri digər riyazi obyektlərdən daha da fərqləndirmək üçün xüsusi tipoqrafik üslubdan, adətən, qalın şriftdən (kursiv olmayan) istifadə edirlər. Alternativ işarələmə qalın şriftli və ya qalın şriftsiz dəyişənin adı ilə ikiqat alt xəttdən istifadəni özündə əks etdirir (məsələn, ${\displaystyle {\underline {\underline {A}}}}$ kimi).

A matrisinin i-ci sətir və j-ci sütunundakı element bəzən matrisin i, j, (i, j) və ya (i, j)-ci elementi kimi nəzərdə tutulur və çox vaxt a_{i, j} və ya a_ij kimi işarə olunur. Bu element üçün başqa bir işarələmə A[i, j] və ya A_{i, j} kimidir. Məsələn, aşağıdakı A matrisinin (1,3) elementi 5-dir (o həmçinin a₁₃, a_1,3, A[1,3] və ya A_1,3 ilə işarə olunur):

${\displaystyle \mathbf {A} ={\begin{bmatrix}4&-7&\color {red}{5}&0\\-2&0&11&8\\19&1&-3&12\end{bmatrix}}}$

Bəzən matrisin elementləri a_{i, j} = f(i, j) şəklindəki düsturla müəyyən edilə bilər. Məsələn, aşağıdakı A matrisinin hər bir elementi a_ij = i − j düsturu ilə müəyyən edilir.

${\displaystyle \mathbf {A} ={\begin{bmatrix}0&-1&-2&-3\\1&0&-1&-2\\2&1&0&-1\end{bmatrix}}}$

Bu halda matrisin özü bəzən düzbucaqlı və ya dairəvi mötərizə daxilində həmin düsturla müəyyən edilir. Məsələn, yuxarıdakı matris A = [i−j] və ya A = ((i−j)) kimi təyin olunur. Əgər matrisin ölçüsü m × n kimi olarsa, yuxarıda qeyd olunan f(i, j) düsturu istənilən i = 1, …, m və istənilən j = 1, …, n üçün etibarlıdır. Bunu ayrıca şəkildə, ya da aşağı indeksdə matrisin ölçüsünü (m × n) göstərməklə ifadə etmək olar. Məsələn, yuxarıdakı A matrisi 3 × 4 ölçülüdür və A = [i − j] (i = 1, 2, 3; j = 1, …, 4) və ya A = [i − j]_3×4 kimi müəyyən edilə bilər.

Bəzi proqramlaşdırma dilləri m-×-n matrisini təsvir etmək üçün ikiqat indeksli massivlərdən (və ya massivlərin massivlərindən) istifadə edir. Bəzi proqramlaşdırma dilləri massivin indekslərinin nömrələnməsinə sıfırdan başlayır, bu halda m × n matrisinin ünsürləri 0 ≤ i ≤ m − 1 və 0 ≤ j ≤ n − 1 ilə indekslənir. Bu məqalədə sadalamanın 1-dən başlayan riyazi yazılışda daha çox yayılmış qaydaya əməl edilir.

Matrisdəki bütün sətir və ya sütunlara istinad etmək üçün bəzən ulduz işarəsindən istifadə edilir. Məsələn, a_i,∗A-nın i-ci sətirinə, a_{∗, j} isə A-nın j-ci sütununa aiddir. m × n ölçülü bütün həqiqi matrislər çoxluğu çox zaman ${\displaystyle {\mathcal {M}}(m,n)}$ və ya ${\displaystyle {\mathcal {M}}_{m\times n}\mathbb {R} }$ kimi işarə olunur. Başqa bir meydan və ya R halqası üzərindəki bütün m × n matrislərinin çoxluğu oxşar şəkildə ${\displaystyle {\mathcal {M}}(m,n,R)}$ və ya ${\displaystyle {\mathcal {M}}_{m\times n}\mathbb {R} }$ işarə olunur. m = n olduqda, yəni matris kvadrat olan halda ölçü təkrarlanmır: ${\displaystyle {\mathcal {M}}(n,R)}$ və ya ${\displaystyle {\mathcal {M}}_{n}(R)}$. Çox vaxt ${\displaystyle M}$ əvəzinə ${\displaystyle {\mathcal {M}}}$-dən istifadə olunur.

Əsas əməllər

Matrislər üzərində dəyişikliklər aparmaq üçün tətbiq oluna bilən bir sıra əsas əməllər mövcuddur ki, bunlara matrislərin

Xarici video
	Matrisləri necə təşkil etmək, toplamaq və vurmaq olar – Bill Shillito, TED ED

toplanması, skalyara (ədədə) vurma, transponirə etmə, matrislərin hasili, sıra əməlləri və altmatris aiddir.

Toplama, skalyara vurma və transponirə etmə

Əməl	Tərif	Nümunə
Toplama	Eyni (m×n) ölçülü matrislərin cəmi həmin ölçülü başqa bir matrisi verir: (A + B)i,j = Ai,j + Bi,j, burada 1 ≤ i ≤ m və 1 ≤ j ≤ n.	${\displaystyle {\begin{bmatrix}1&3&1\\1&0&0\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\end{bmatrix}}={\begin{bmatrix}1+0&3+0&1+5\\1+7&0+5&0+0\end{bmatrix}}={\begin{bmatrix}1&3&6\\8&5&0\end{bmatrix}}}$
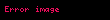Skalyara (ədədə) vurma	c ədədi (abstrakt cəbr dilində skalyar da deyilir) və A matrisinin cA hasili A-nın hər bir elementi c-yə vurulmaqla hesablanır: (cA)i, j = c · Ai, j.	${\displaystyle 2\cdot {\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot {(-3)}\\2\cdot 4&2\cdot {(-2)}&2\cdot 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}}$
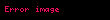Transponirə etmə	m x n ölçülü A matrisinin bütün sətirləri ilə sütunlarının yerlərinin dəyişdirilməsiylə (nömrələrini saxlamaqla) alınan n x m ölçülü A^T (həmçinin A^tr, A^t və ya A' ilə işarələnir) matrisi: (A^T)i, j = Aj, i.	${\displaystyle {\begin{bmatrix}1&2&3\\0&-6&7\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&0\\2&-6\\3&7\end{bmatrix}}}$

Ədədlərin məlum xassələri matrislər üzərindəki əməllərə də şamil edilir: məsələn, toplama kommutativdir, yəni matrislərin cəmi toplananların ardıcıllığından asılı deyil: A + B = B + A. Transponirə etmə (cA)^T = c(A^T) və (A + B)^T = A^T + B^T ilə ifadə olunduğu kimi toplama və skalyara vurma ilə uzlaşır.

Matrislərin vurulması

İki matris hasilinin sxematik təsviri.

İki matrisin hasili o halda təyin edilir ki, soldakı matrisin sütunlarının sayı sağdakı matrisin sətirlərinin sayı ilə eyni olsun. m × n ölçülü A matrisinin n × p ölçülü B matrisinə hasili hədləri

${\displaystyle [\mathbf {AB} ]_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots +a_{i,n}b_{n,j}=\sum _{r=1}^{n}a_{i,r}b_{r,j},}$

kimi təyin olunan AB matrisinə deyilir. Burada 1 ≤ i ≤ m və 1 ≤ j ≤ p. Məsələn, hasildə altından xətt çəkilmiş 2340 elementi aşağıdakı kimi hesablanır

(2 × 1000) + (3 × 100) + (4 × 10) = 2340:

${\displaystyle {\begin{aligned}{\begin{bmatrix}{\underline {2}}&{\underline {3}}&{\underline {4}}\\1&0&0\\\end{bmatrix}}{\begin{bmatrix}0&{\underline {1000}}\\1&{\underline {100}}\\0&{\underline {10}}\\\end{bmatrix}}&={\begin{bmatrix}3&{\underline {2340}}\\0&1000\\\end{bmatrix}}.\end{aligned}}}$

Matrislərin hasili (AB)C = A(BC) (assosiativlik) və (A + B)C = AC + BC, eləcə də C(A + B) = CA + CB (sola və sağa nəzərən distributivlik) qanununa cavab verir, bu zaman matrislərin ölçüsü elə olmalıdır ki, müxtəlif hasillər təyin oluna bilsin.

AB hasili BA təyin edilmədən müəyyən edilə bilər, yəni A və B müvafiq olaraq mxn və nxk ölçülü matrislərdirsə və m ≠ k olarsa. Hər iki hasil müəyyən edilsə belə, onların ümumiyyətlə bərabər olmasına ehtiyac yoxdur, yəni:

AB ≠ BA

Başqa sözlə, hasili vuruqların sırasından asılı olmayan (rasional, həqiqi və ya kompleks) ədədlərdən fərqli olaraq, matrislər vurmaya nəzərən kommutativ deyil.

${\displaystyle {\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}{\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}={\begin{bmatrix}0&1\\0&3\\\end{bmatrix}},}$

halbuki

${\displaystyle {\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}{\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}={\begin{bmatrix}3&4\\0&0\\\end{bmatrix}}.}$

Matrislərin adi formada vurulması ilə yanaşı, vurulan matrislər üzərində daha az istifadə olunan Adamar və Kroneker hasili kimi digər əməllər də mövcuddur. Onlar Silvestr tənliyi kimi matris tənliklərinin həlli zamanı ortaya çıxır.

Sətir əməlləri

Üç növ sətir əməli var:

1. sətirlərin toplanması, yəni bir sətir digəri ilə toplana bilər;
2. sətirlərin vurulması, yəni sətirin bütün elementlərini sıfırdan fərqli sabitə vurmaq olar;
3. sətirlərin yerdəyişməsi, yəni matrisin iki sətirini dəyişdirmək olar.

Bu əməllər xətti tənliklərin həlli və matrisin tərsinin tapılması da daxil olmaqla müxtəlif şəkillərdə istifadə olunur.

Altmatris

Hər hansı bir matrisin altmatrisi istənilən sətir və/və ya sütunlar yığımının silinməsi ilə əldə edilir.

Məsələn, aşağıdakı 3x4 ölçülü matrisin 3-cü sətir və 2-ci sütununu silməklə 2x3 ölçülü altmatris düzəltmək olar:

${\displaystyle \mathbf {A} ={\begin{bmatrix}1&\color {red}{2}&3&4\\5&\color {red}{6}&7&8\\\color {red}{9}&\color {red}{10}&\color {red}{11}&\color {red}{12}\end{bmatrix}}\rightarrow {\begin{bmatrix}1&3&4\\5&7&8\end{bmatrix}}.}$

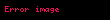
Matrisin minor və cəbri tamamlayıcıları müəyyən altmatrislərin determinantını hesablamaqla tapılır.

Əsas altmatris müəyyən sətir və sütunları silməklə əldə edilən kvadrat altmatrisdir. Onun tərifi müəllifdən müəllifə dəyişir. Bəzi müəlliflərə görə, əsas altmatris, qalan sətir indeksləri çoxluğu ilə qalan sütun indeksləri çoxluğu eyni olan altmatrisdir. Digər müəlliflər əsas matrisi bəzi k ədədləri üçün ilk k sətir və sütunundan geridə qalanlardan ibarət matris kimi təyin edir; bu tip submatris həm də aparıcı əsas submatris adlanır.

Xətti tənliklər

Matrislər bir çox xətti tənlikləri, yəni xətti tənliklər sistemini yığcam şəkildə yazmaq və onlarla işləmək üçün istifadə edilə bilər. Məsələn, A mxn ölçülü matris, x x₁, x₂, …, x_n dəyişənlərindən ibarət sütun vektoru (yəni n×1 ölçülü matris), b isə m×1 ölçülü sütun vektorudursa, onda

${\displaystyle \mathbf {Ax} =\mathbf {b} }$

matris tənliyi

${\displaystyle {\begin{aligned}a_{1,1}x_{1}+a_{1,2}x_{2}+&\cdots +a_{1,n}x_{n}=b_{1}\\&\ \ \vdots \\a_{m,1}x_{1}+a_{m,2}x_{2}+&\cdots +a_{m,n}x_{n}=b_{m}\end{aligned}}}$

xətti tənliklər sisteminə ekvivalentdir.

Bütün bu tənlikləri ayrı-ayrılıqda yazmaq əvəzinə matrislərdən istifadə etməklə daha yığcam şəkilə salmaq və həll etmək olar. Əgər n = m və tənliklər sərbəst olarsa, bunu aşağıdakı şəkildə yazmaqla tamamlamaq olar

${\displaystyle \mathbf {x} =\mathbf {A} ^{-1}\mathbf {b} }$

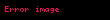
burada A⁻¹A matrisinin tərsidir.

Əgər A-nın tərsi yoxdursa, onun ümumiləşdirilmiş tərsindən istifadə etməklə həllər (əgər varsa) tapıla bilər.

Xətti çevirmələr

2x2 ölçülü matrislə göstərilən vektorlar paraleloqrama çevrilmiş vahid kvadratın tərəflərinə uyğun gəlməkdədir.

Matrislər və matrislərin hasili xətti çevirmələrlə əlaqəli olduqda onların əsas cəhətləri ortaya çıxır. mxn ölçülü həqiqi A matrisi Rⁿ-dəki hər bir x vektorunu R^m-də vektor olan Ax (matris) hasilinə qarşı qoyan Rⁿ → R^m xətti çevirməsinə səbəb olur. Digər tərəfdən, hər bir f: Rⁿ → R^m xətti çevirməsi mxn ölçülü unikal A matrisindən yaranır: aşkar şəkildə A-nın (i, j)-elementi f(e_j)-nin i-ci koordinatıdır (burada e_j = (0,…,0,1,0,…,0) j-ci mövqedə 1 və başqa yerlərdə 0 qiymətini alan vahid vektordur). Bu zaman deyilir ki, A matrisi f xətti çevirməsini təmsil edir, A isə f-in çevirmə matrisi adlanır.

Məsələn, 2×2 ölçülü

${\displaystyle \mathbf {A} ={\begin{bmatrix}a&c\\b&d\end{bmatrix}}}$

matrisinə vahid kvadratın təpələri (0, 0), (a, b), (a + c, b + d) və (c, d) olan paraleloqrama çevrilməsi kimi baxıla bilər. Sağda təsvir olunan paraleloqram A-nı növbə ilə ${\displaystyle {\begin{bmatrix}0\\0\end{bmatrix}},{\begin{bmatrix}1\\0\end{bmatrix}},{\begin{bmatrix}1\\1\end{bmatrix}}}$ və ${\displaystyle {\begin{bmatrix}0\\1\end{bmatrix}}}$ sütun vektorlarının hər birinə vurmaqla əldə edilir. Bu vektorlar vahid kvadratın təpə nöqtələrini müəyyən edir.

Aşağıdakı cədvəl R² ilə əlaqəli xətti çevirmələr vasitəsilə 2×2 ölçülü müxtəlif həqiqi matrisləri nümayiş etdirir. Mavi rəngli orijinal yaşıl tor və fiqurlara çevrilir. Koordinat başlanğıcı (0,0) qara nöqtə ilə qeyd olunmuşdur.

Üfüqi sürüşmə [m = 1.25]	Şaquli oxa nəzərən əksetmə	Sıxmaqla çevirmə [r = 3/2]	Miqyaslanma [3/2 nisbətdə]	Dönmə [π/6 = 30° qədər]
${\displaystyle {\begin{bmatrix}1&1.25\\0&1\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}-1&0\\0&1\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {2}{3}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {3}{2}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}\cos \left({\frac {\pi }{6}}\right)&-\sin \left({\frac {\pi }{6}}\right)\\\sin \left({\frac {\pi }{6}}\right)&\cos \left({\frac {\pi }{6}}\right)\end{bmatrix}}}$

Matrislər və xətti çevirmələr arasında birəbir uyğunluq (biyeksiya) altında matrislərin vurulması çevirmələrin kompozisiyasına uyğun gəlir: əgər kxm ölçülü matris B başqa bir xətti çevirməni təmsil edirsə: R^m → R^k, onda g ∘ f kompozisiyası BA ilə ifadə edilir, çünki

(g ∘ f) (x) = g(f(x)) = g(Ax) = B(Ax) = (BA)x.

Son bərabərlik matrislərin vurmaya görə assosiativliyindən irəli gəlir.

A matrisinin ranqı matrisin xətti sərbəst sətir vektorlarının maksimum sayıdır və bu, xətti sərbəst sütun vektorlarının maksimum sayına bərabərdir. Ekvivalent olaraq bu, A ilə ifadə olunan xətti çevirmənin obrazının ölçüsüdür. Ranq-sıfırlıq teoremi göstərir ki, matrisin nüvəsinin ölçüsü və ranqı matrisin sütunları sayına bərabərdir.

Kvadrat matris

Kvadrat matris bərabər sayda sətir və sütuna malik matrisdir. nxn ölçülü matris n tərtibli kvadrat matris adlanır. Tərtibləri bərabər olan istənilən iki kvadrat matris toplanıla və vurula bilər. a_ii elementləri kvadrat matrisin baş diaqonalını təşkil edir. Onlar matrisin yuxarı sol küncünü aşağı sağ küncü ilə birləşdirən xəyali xətt üzrə yerləşirlər.

Başlıca növləri

Diaqonal və üçbucaq matris

Adı	Nümunə (n = 3)
Diaqonal matris	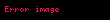${\displaystyle {\begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\\\end{bmatrix}}}$
Aşağı üçbucaq matris	${\displaystyle {\begin{bmatrix}a_{11}&0&0\\a_{21}&a_{22}&0\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}}$
Yuxarı üçbucaq matris	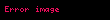${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&0&a_{33}\\\end{bmatrix}}}$

Əgər A-nın baş diaqonaldan aşağıda duran bütün elementləri sıfırdırsa, A yuxarı (yaxud sağ) üçbucaq matris adlanır. Eynilə, A-nın baş diaqonaldan yuxarıda duran bütün elementləri sıfırdırsa, A aşağı (yaxud sol) üçbucaq matris adlanır. Baş diaqonal elementlərindən başqa qalan elementlər sıfırdırsa, A diaqonal matris adlanır.

Vahid matris

n ölçülü vahid matris baş diaqonaldakı bütün elementləri 1-ə, digər elementləri isə 0-a bərabər olan nxn ölçülü matrisdir. Məsələn,

${\displaystyle \mathbf {I} _{1}={\begin{bmatrix}1\end{bmatrix}},\ \mathbf {I} _{2}={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\ \ldots ,\ \mathbf {I} _{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}}$

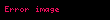
Bu n tərtibli kvadrat matrisdir, həmçinin diaqonal matrisin xüsusi növüdür. Ona vahid matrisi deyilir, çünki hər hansı matrisin onunla hasili elə həmin matrisi verir, yəni mxn ölçülü hər hansı A matrisi üçün

AI_n = I_mA = A

bərabəriyi doğrudur.

Vahid matrisin sıfırdan fərqli skalyarla hailinə skalyar matris deyilir. Əgər matrisin elementləri meydandan gəlirsə, skalyar matrislər matrislərin vurulması altında qrup təşkil edir, yəni meydanın sıfırdan fərqli elementlərinin multiplikativ qrupuna izomorfdur.

Simmetrik və ya çəp-simmetrik matris

Transponirə edildikdə özü alınan, yəni A=A^T olan A matrisinə simmetrik matris deyilir. Bunun əvəzinə, A= −A^T olduqda, A matrisinə çəpsimmetrik matris deyilir. Kompleks matrislərdə simmetriya çox vaxt A^∗=A bərabərliyini təmin edən Ermit matrisi anlayışıyla əvəz olunur, burada ulduz işarəsi A matrisinin Ermit və ya transponirə edilmiş kompleks qoşmasını bildirir.

Spektral teoremə görə, həqiqi simmetrik matrislər və kompleks Ermit matrisləri məxsusi bazisə malikdir; yəni hər bir vektor məxsusi vektorların xətti kombinasiyası kimi ifadə edilə bilər. Hər iki halda bütün məxsusi qiymətlər həqiqidir. Bu teorem sonsuz sayda sətir və sütuna malik matrislərlə əlaqəli olan sonsuz ölçülü hallar üçün ümumiləşdirilə bilər (aşağıya baxın).

Tərs matris və onun tərsi

Aşağıdakı bərabərliyi ödəyən B matrisi varsa, A kvadrat matrisinə tərsi olan və ya qeyri-sinqulyar matris deyilir:

AB = BA = I_n

burada I_n baş diaqonalında 1-lər və qalan yerlərdə 0-lar yerləşən n×n ölçülü vahid matrisdir. Əgər B mövcuddursa, o yeganədir və A-nın tərs matrisi adlanır, həmçinin A⁻¹ ilə göstərilir.

Müəyyən matris

Müsbət müəyyən matris	Qeyri-müəyyən matris
${\displaystyle {\begin{bmatrix}{\frac {1}{4}}&0\\0&1\\\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\frac {1}{4}}&0\\0&-{\frac {1}{4}}\end{bmatrix}}}$
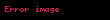Q(x, y) = 1/4 x^2 + y^2	Q(x, y) = 1/4 x^2 − 1/4y^2
Elə nöqtələr var ki, Q(x,y)=1 (Ellips).	Elə nöqtələr var ki, Q(x,y)=1 (Hiperbola).

Simmetrik həqiqi A matrisi, o zaman müsbət-müəyyən adlanır ki, onunla əlaqəli

f (x) = x^TA x

kvadratik forması Rⁿ-dəki sıfırdan fərqli hər bir x vektoru üçün müsbət qiymətlər alsın. f (x) yalnız mənfi qiymətlər aldıqda, A-ya mənfi-müəyyən; həm mənfi, həm də müsbət qiymətlər aldıqda isə qeyri-müəyyən matris deyilir. Əgər f kvadratratik forması yalnız mənfi olmayan qiymətlər (müsbət və ya sıfır) alırsa, simmetrik matris müsbət-yarımüəyyən adlanır (əksinə olduqda isə mənfi-yarımüəyyən); deməli, matris nə müsbət-yarımmüəyyən, nə də mənfi-yarımmüəyyən olmadıqda qeyri-müəyyən olur.

Simmetrik matris, o halda müsbət-müəyyən olur ki, onun bütün məxsusi qiymətləri müsbətdir, yəni matris müsbət-yarımüəyyəndir və onun tərsi var. Sağdakı cədvəldə 2x2 ölçülü matrislər üçün iki mümkün hal göstərilmişdir.

Sərbəst dəyişənin yerinə iki müxtəlif vektor yazılarsa A ilə əlaqəli bixətti forma alınar:

B_A (x, y) = x^TAy

Matrislərin kompleks olması halında da eyni terminologiya və nəticə tətbiq edilir, simmetrik matris, kvadratik forma, bixətti forma və x^Tçevrilməsi müvafiq olaraq Ermit matris, Ermit forma, bir yarım-xətti forma və x^H qoşma çevrilməsi ilə əvəz olunur.

Ortoqonal matris

Sütun və sətirləri ortoqonal vahid vektorlar (yəni ortonormal vektorlar) olan həqiqi elementli kvadrat matrisə ortoqonal matris deyilir.

Ekvivalent olaraq, A matrisi transponirə edildikdə onun tərsi alınırsa, o ortoqonaldır:

${\displaystyle \mathbf {A} ^{\mathrm {T} }=\mathbf {A} ^{-1},\,}$

buradan alınır ki,

${\displaystyle \mathbf {A} ^{\mathrm {T} }\mathbf {A} =\mathbf {A} \mathbf {A} ^{\mathrm {T} }=\mathbf {I} _{n},}$

burada I_n n ölçüsünün vahid matrisidir.

Ortoqonal A matrisi mütləq şəkildə tərslənən (A⁻¹ = A^T), unitar (A⁻¹ = A*) və normaldır (A*A = AA*). İstənilən ortoqonal matrisin determinantı ya +1, ya da −1-dir. Determinantı +1 olan ortoqonal matrisə xüsusi ortoqonal matris deyilir. Xətti çevirmə olaraq, determinantı +1 olan hər bir ortoqonal matris əksetməsiz xalis dönmədir, yəni çevirmə çevrilmiş strukturun oriyentasiyasını saxlayır, determinantı −1 olan hər bir ortoqonal matris isə oriyentasiyanı tərsinə çevirir, yəni xalis əksetmə və (ehtimal ki, sıfır) dönmənin kompozisiyasıdır. Vahid matrislərin determinantı 1-ə bərabər olur və onlar sıfır bucaq qədər xalis dönmələrdir.

Ortoqonal matrisin kompleks analoqu unitar matrisdir.

Başlıca əməllər

İz

A kvadrat matrisinin izi (tr A) dedikdə, onun diaqonal elementlərinin cəmi başa düşülür. Matrislərin vurulması yuxarıda qeyd edildiyi kimi kommutativ olmasa da, iki matrisin hasilinin izi vuruqların sırasından asılı deyil:

tr(AB) = tr(BA).

Bu bilavasitə matrislərin vurulmasından irəli gəlir:

${\displaystyle \operatorname {tr} (\mathbf {AB} )=\sum _{i=1}^{m}\sum _{j=1}^{n}a_{ij}b_{ji}=\operatorname {tr} (\mathbf {BA} ).}$

Buradan belə çıxır ki, ikidən artıq matrisin hasilinin izi matrislərin siklik permutasiyalarından asılı deyil, lakin bu, ümumiyyətlə, ixtiyari permutasiyalara şamil edilmir (məsələn, ümumi halda tr(ABC) ≠ tr(BAC)). Həmçinin, matrisin izi onun transponirəsinin izinə bərabərdir:

tr(A) = tr(A^T).

Determinant

Göstərilən matris tərəfindən verilən R² üzərində xətti çevirmə. Bu matrisin determinantı −1-dir, çünki sağdakı yaşıl paraleloqramın sahəsi 1-dir, lakin qarşı qoyma vektorların saat əqrəbinin əksinə istiqamətini saat əqrəbinin əqrəbinə çevirdiyi üçün oriyentasiyanı tərsinə çevirir.

Kvadrat A matrisinin determinantı (det(A) və ya |A|) həmin matrislə əlaqəli ədəddir. Hər hansı bir matrisin tərsi yalnız və yalnız onun determinantı sıfırdan fərqli olduqda mövcud ola bilər. Onun mütləq qiyməti vahid kvadratın (və ya kubun) obrazının sahə (R²-də) və ya həcminə (R³-də) bərabər olub, işarəcə müvafiq xətti çevirmənin oriyentasiyasına uyğundur: determinant yalnız və yalnız oriyentasiya qorunub saxlanılan zaman müsbət olur.

2x2 ölçülü matrisin determinantı aşağıdakı şəkildə təyin olunur:

${\displaystyle \det {\begin{bmatrix}a&b\\c&d\end{bmatrix}}=ad-bc.}$

3x3 ölçülü matrislərin determinantı 6 həddə malik olur (Sarrius qaydası). Daha uzun Leybnits düsturu bu iki düsturu bütün ölçülər üçün ümumiləşdirir.

Kvadrat matrislər hasilinin determinantı onların determinantları hasilinə bərabərdir:

det(AB) = det(A) · det(B).

Determinantın hər hansı bir sətir (sütun) elementlərini müəyyən bir ədədə vurub başqa sətrin (sütunun) uyğun elementləri ilə topladıqda onun qiyməti dəyişməz. Determinantın iki sətrinin və ya iki sütununun yerlərini dəyişsək, onun yalnız işarəsi dəyişər. Bu əməllərdən istifadə etməklə istənilən matrisi aşağı (və ya yuxarı) üçbucaq matrisə çevirmək olar və belə matrislər üçün determinant baş diaqonal elementlərinin hasilinə bərabərdir; bu hər hansı matrisin determinantını hesablamaq üçün bir üsul təqdim edir. Nəhayət, Laplas teoremi determinantı minorlar, yəni daha kiçik ölçülü matrislərin determinantları vasitəsilə ifadə edir. Bu genişlənmə determinantların rekursiv tərifi üçün istifadə edilə(başlanğıc hal kimi onun yeganə elementi olan 1x1 ölçülü matrisin determinantını və ya hətta 1-ə bərabər olan 0x0 ölçülü matrisin determinantını götürməklə), beləliklə bunun Leybnits düsturuna ekvivalent olduğu görülə bilər. Determinantlardan Kramer qaydasından istifadə edərək xətti sistemləri həll etmək üçün istifadə edilə bilər, burada iki əlaqəli kvadrat matrisin determinantlarının bölünməsi sistemin dəyişənlərinin hər birinin qiymətinə bərabərdir.

Məxsusi qiymətlər və məxsusi vektorlar

λ ədədi və sıfırdan fərqli v vektoru

${\displaystyle Av=\lambda v}$

bərabərliyini ödədikdə, müvafiq olaraq onlara A-nın məxsusi qiyməti və məxsusi vektoru deyilir. λ ədədi n×n ölçülü A matrisinin məxsusi qiymətidir, o halda və yalnız A−λI_n o ifadəsinin tərsi olmasın. Bu aşağıdakı bərabərliyə ekvivalentdir:

${\displaystyle \det(\mathbf {A} -\lambda \mathbf {I} )=0.}$

det(XI_n−A) determinantının qiymətləndirilməsi ilə verilən qeyri-müəyyən X-dəki p_A çoxhədlisi A-nın xarakteristik çoxhədlisi adlanır. Bu n dərəcəli monik çoxhədlidir. Buna görə də p_A(λ) = 0 çoxhədli tənliyinin ən çoxu n müxtəlif həlli var, belə ki, matris məxsusi qiymətlərə malikdir. A-nın elementləri həqiqi olsa belə, onlar kompleks ola bilər. Keli-Hamilton teoreminə görə, p_A(A) = 0 olur, yəni matris öz xarakteristik çoxhədlisi ilə əvəz edildikdə nəticə sıfır matris olur.

Hesablama aspektləri

Matris hesablamaları çox vaxt müxtəlif üsullarla həyata keçirilə bilər. Bir çox problem həm birbaşa alqoritmlər, həm də iterativ yanaşmaların köməyilə həll edilə bilər. Məsələn, kvadrat matrisin məxsusi vektorları, n sonsuzluğa yaxınlaşdıqda məxsusi vektora yaxınlaşan x_n vektorlar ardıcıllığını tapmaqla əldə edilə bilər.

Hər bir konkret problemə görə ən uyğun alqoritmi seçmək üçün bütün mövcud alqoritmlərin həm effektivliyini, həm də dəqiqliyini müəyyən etmək vacibdir. Bu məsələləri öyrənən sahə ədədi xətti cəbr adlanır. Digər ədədi vəziyyətlərdə olduğu kimi, iki əsas cəhət alqoritmlərin kompleksliyi və ədədi stabilliyidir.

Alqoritmin mürəkkəbliyini müəyyən etmək yuxarı hədləri tapmaq və ya bəzi alqoritmi yerinə yetirmək üçün skalyarların toplanması və vurulması kimi neçə elementar əməlin, məsələn, matrislərin vurulmasının zəruri olduğunun təxminlərini tapmaq deməkdir. Yuxarıda verilmiş tərifdən istifadə edərək iki nxn ölçülü matrisin hasilini hesablamaq üçün n³ vurma lazımdır, çünki hasilin n² elementlərindən hər hansı biri üçün n vurma lazımdır. Strassen alqoritmi bu "sadəlövh" alqoritmi üstələyir; ona yalnız n^2.807 vurma lazımdır. Təkmilləşdirilmiş yanaşma hesablama cihazlarının spesifik xüsusiyyətlərini də özündə birləşdirir. Bir çox praktik hallarda əlaqəli matrislər haqqında əlavə bilgilər məlum olur. Mühüm hal seyrək matrislərlə, yəni elementlərinin çoxu sıfır olan matrislərlə bağlıdır. Ax = b şəklindəki xətti tənliklər sistemini seyrək A matrisinə görə həll etmək üçün qoşma qradiyent metodu kimi xüsusi uyğunlaşdırılmış alqoritmlər mövcuddur.

Giriş qiymətlərindəki kiçik sapmalar nəticədə böyük sapmalara səbəb olmursa, alqoritm kobud formada desək, ədədi stabildir. Məsələn, Laplas teoremi vasitəsilə matrisin tərsinin hesablanması (adj(A) A-nın qarşılıqlı matrisini ifadə edir)

A⁻¹ = adj(A) / det(A)

matrisin determinantı çox kiçik olarsa, nəzərə çarpan yuvarlaqlaşdırma xətalarına səbəb ola bilər. Matrisin norması xətti cəbri məsələlərin şərtləndirilməsini, məsələn, matrisin tərsini hesablamaq üçün istifadə edilə bilər.

Əksər kompüter proqramlaşdırma dilləri massivləri dəstəkləyir, lakin matrislər üçün daxili əmrlərlə tərtib edilməyib. Bunun əvəzinə, mövcud xarici kitabxanalar, demək olar ki, bütün hazırda istifadə olunan proqramlaşdırma dillərində massivlərdə matris əməliyyatları təmin edir. Matris manipulyasiyası kompüterlərin ilk ədədi tətbiqləri arasında idi. Orijinal Dartmouth BASIC -də 1964-cü ildə ikinci buraxılışından etibarən massivlər üzərində matris arifmetikası üçün daxili əmrlər var idi. Hələ 1970-ci illərdə HP 9830 kimi bəzi mühəndis stolüstü kompüterlərində matrislər üçün BASIC əmrləri əlavə etmək üçün ROM kartricləri var idi. APL kimi bəzi kompüter dilləri matrisləri manipulyasiya etmək üçün nəzərdə tutulmuşdur və matrislərlə hesablamalara kömək etmək üçün müxtəlif riyazi proqramlardan istifadə edilə bilər.

Dekompozisiya

Matrisləri daha rahat formada göstərmək üçün bir neçə üsul var. Bunlar, ümumiyyətlə, matrisin dekompozisiyası və ya vuruqlara ayırma üsulu adlanır. Bütün bu üsulların marağı ondan ibarətdir ki, onlar sözügedən matrislərin determinantı, ranqı və ya tərsi kimi müəyyən xassələri qoruyub saxlayırlar ki, bu kəmiyyətlər çevirmənin tətbiqindən sonra hesablana bilsin və ya bəzi növ matrislər üçün müəyyən matris əməllərinin həyata keçirilməsi alqoritmik olaraq daha asan olsun.

LU-dekompozisiya matrisləri aşağı (L) və yuxarı üçbucaq matrislərin (U) hasili kimi verilir. Bu dekompozisiya hesablandıqdan sonra xətti sistemlər irəli və geri əvəzetmə adlanan sadə metodla daha səmərəli formada həll edilə bilər. Eyni şəkildə, üçbucaqlı matrislərin tərslərini hesablamaq alqoritmik olaraq daha asandır. Qauss üsulu oxşar alqoritmə əsaslanır; istənilən matrisi sətir pilləli formaya çevirir. Hər iki üsul matrisi sətir və ya sütunların dəyişdirilməsinə uyğun gələn uyğun elementar matrislərə vurmaqla davam edir və bir sətiri müəyyən ədədə vurub digər sətirlə toplanılır. Sinqulyar ayrılma istənilən A matrisini UDV^∗ hasili kimi ifadə edir, burada U və V unitar, D isə diaqonal matrisdir.

Matrisin Jordan (normal) formasına dair nümunə. Boz bloklara Jordan blokları deyilir.

Məxsusi dekompozisiya və ya diaqonallaşdırma A-nı VDV⁻¹ hasili kimi ifadə edir, burada D diaqonal, V isə uyğun tərslənən matrisdir. Əgər A matrisini bu formada yazmaq mümkündürsə, ona diaqonallaşdırıla bilən matris deyilir. Daha ümumi şəkildə və bütün matrislərə aid olan Jordan ayrılması matrisi normal formaya (Jordan formasına) çevirir, yəni yalnız sıfırdan fərqli elementləri əsas diaqonalda yerləşdirilən A-nın λ₁-dən λ_n-ə qədər olan məxsusi qiymətləri olan matrisləri, sağda göstərildiyi kimi əsas diaqonalın üstündə yerləşdirilir və ola bilsin ki, ünsürlər birbaşa baş diaqonalın üzərində birinə bərabər olan matrislərdir. Məxsusi dekompozisiyanı nəzərə almaqla, A-nın n-ci dərəcəsini (yəni, matrislərin n dəfə özünə vurulması) aşağıdakı üsulla hesablamaq olar

Aⁿ = (VDV⁻¹)ⁿ = VDV⁻¹VDV⁻¹…VDV⁻¹ = VDⁿV⁻¹

Və diaqonal matrisin qüvvətini diaqonal elementlərinin müvafiq qüvvətləri götürməklə hesablamaq olar, bu, A matrisinin eksponentini hesablamaqla müqayisədə daha asandır. Bu, xətti diferensial tənliklərin, matris loqarifmlərinin və matrislərin kvadrat köklərinin həllində çox vaxt ehtiyac duyulan eksponensial e^A matrisini hesablamaq üçün istifadə edilə bilər. Ədədi mənada gözlənilməz hallardan yayınmaq üçün Şur dekompozisiyası kimi əlavə alqoritmlərdən istifadə edilə bilər.

Abstrakt cəbri aspektlər və ümumiləşdirmələr

Matrislər müxtəlif yollarla ümumiləşdirilə bilər. Abstrakt cəbr daha ümumi sahələrə və ya hətta halqalara daxil olan matrislərdən istifadə edir, xətti cəbr isə xətti çevirmələr anlayışı daxilində matrislərin xassələrini sistemləşdirir. Sonsuz sayda sütun və sətirlərə malik matrisləri nəzərdən keçirmək mümkün olur. Başqa bir uzantı, vektorlardan fərqli olaraq, daha yüksək ölçülü ədədlər yığımı kimi baxıla bilən tenzorlardır, bunlar çox vaxt ədədlərin ardıcıllığı kimi həyata keçirilə bilər, matrislər isə düzbucaqlı və ya ikiölçülü ədədlər yığımıdır. Müəyyən tələblərə tabe olan matrislər matris qrupları kimi tanınan qrupları meydana gətirirlər. Eynilə müəyyən şərtlərdə matrislər matris halqaları kimi tanınan halqalar əmələ gətirir. Matrislərin hasilinin ümumi kommutativ olmasa da, müəyyən matrislər matris meydanları kimi tanınan meydanları əmələ gətirir.

Daha ümumi elementlərə malik matrislər

Bu məqalədə elementləri həqiqi və ya kompleks ədədlər olan matrislərə diqqət yetirilir. Bununla belə, həqiqi və ya kompleks ədədlərdən başqa, daha ümumi elementlərə malik olan matrisləri də nəzərdən keçirmək olar. Ümumiləşdirmənin ilk addımı kimi, R və ya C yerinə hər hansı bir meydan, yəni toplama, çıxma, vurma və bölmə əməlləri təyin edildiyi və düzgün aparıldığı çoxluq, məsələn, rasional ədədlər və ya sonlu meydanlar istifadə edilə bilər. Məsələn, kodlaşdırma nəzəriyyəsində sonlu meydanlar üzərindəki matrislərdən istifadə edilir. Məxsusi qiymətlər çoxhədlinin kökləri kimi nəzərə alındıqda, onlar yalnız matrisin elementlərindən daha böyük meydanda mövcud ola bilər; məsələn, real elementləri olan matris halında onlar kompleks ola bilər. Matrisin elementlərini daha böyük meydanın elementləri kimi yenidən şərh etmək imkanı (məsələn, həqiqi matrisə elementləri hamısı həqiqi olan kompleks matris kimi baxmaq) sonra hər kvadrat matrisin tam məxsusi qiymətlərinə malik olmasını nəzərdən keçirməyə imkan verir. Alternativ olaraq, əvvəldən yalnız C kimi cəbri qapalı meydanda elementləri olan matrisləri nəzərdən keçirmək olar.

Daha ümumi formada, R halqasında elementləri olan matrislər riyaziyyatda geniş istifadə olunur. Halqa anlayışı meydana nəzərən daha ümumi bir anlayışdır ki, burada bölmə əməlinin mövcud olmasına ehtiyac yoxdur. Matrislərin eyni toplama və vurma əməlləri bu parametrə də aiddir. R üzərində bütün kvadrat nxn matrislərin M(n, R) (həmçinin M_n(R)) çoxluğu matris halqasıdır, sol R modulunun R endomorfizm halqasına izomorfdur. Əgər R halqası kommutativdirsə, yəni onun vurulması kommutativdirsə, M(n, R) R üzərində unitar qeyri-kommutativ (n = 1 olmadıqda) assosiativ cəbrdir. Kvadrat matrislərin R kommutativ halqası üzərindəki determinantını hələ də Leybnits düsturundan istifadə etməklə müəyyən etmək olar; belə bir matrisin yalnız və yalnız o halda tərsi var ki, onun determinantı R-də tərslənən olarsa, hər bir sıfırdan fərqli elementin çevrilə bildiyi F meydanı üzərində vəziyyəti ümumiləşdirir. Üst halqalar üzərindəki matrislər supermatrislər adlanır.

Matrislərin bütün elementləri həmişə eyni halqada, hətta ümumiyyətlə hər hansı bir halqada olmur. Xüsusi, lakin ümumi hallardan biri blok matrisləridir ki, bu da elementlərinin özləri matrislər olan matrislər kimi qəbul edilə bilər. Elementlər kvadrat matrislər olmamalıdır və buna görə də hər hansı bir halqanın üzvləri olmamalıdır; lakin onların ölçüləri müəyyən uyğunluq şərtlərinə cavab verməlidir.

Xətti çevirmələrlə əlaqə

Rⁿ → R^m xətti çevirmələri yuxarıda təsvir olunduğu kimi mxn ölçülü matrislərə ekvivalentdir. Daha ümumi şəkildə, sonlu ölçülü vektor fəzaları arasında istənilən f: V → W xətti çevirməsi, V-nin v₁, …, v_n və w₁, …, w_m əsaslarını seçdikdən sonra A = (a_ij) matrisi ilə təsvir edilə bilər. W-nun (beləliklə, n V-nin, m isə W-nun ölçüsüdür), belə ki,

${\displaystyle f(\mathbf {v} _{j})=\sum _{i=1}^{m}a_{i,j}\mathbf {w} _{i}\qquad \ j=1,\ldots ,n.}$

Başqa sözlə, A-nın j sütunu v_j-nin obrazını W-nun w_i bazis vektorları baxımından ifadə edir; beləliklə, bu əlaqə A matrisinin elementlərini yeganə formada müəyyən edir. Matris əsasların seçimindən asılıdır: əsasların müxtəlif seçimləri fərqli, lakin ekvivalent matrislərin yaranmasına səbəb olur. Yuxarıdakı konkret anlayışların bir çoxunu bu işıqda yenidən şərh etmək olar, məsələn, A^T çevrilmiş matrisi ikili əsaslara münasibətdə A tərəfindən verilmiş xətti çevirmənin yerdəyişməsini təsvir edir.

Bu xüsusiyyətlər daha təbii şəkildə yenidən ifadə edilə bilər: kompozisiya olaraq vurma ilə k meydanında elementləri olan bütün matrislərin kateqoriyası sonlu ölçülü vektor fəzalarının və bu meydan üzərində xətti çevirmələrin kateqoriyasına bərabərdir. Daha ümumi olaraq, m×n matrislər çoxluğu birliyə malik ixtiyari R halqası üçün R^m və Rⁿ sərbəst modulları arasında R-xətti çevirmələri göstərmək üçün istifadə edilə bilər. n = m olduqda, bu çevirmələrin kompozisiyası mümkündür və bu, Rⁿ-nin endomorfizm halqasını təmsil edən n× n ölçülü matrislərin matris halqasına səbəb olur.

Matris qrupları

Qrup binar əməllə birlikdə obyektlər toplusundan ibarət riyazi struktur, yəni müəyyən tələblərə uyğun olaraq hər hansı iki obyekti üçüncü ilə birləşdirən əməldir.Obyektləri matrislər və qrup əməli matrislərin vurulması olan qrupa matris qrupu deyilir. Bir qrup hər bir element tərslənən olduğundan, ən ümumi matris qrupları ümumi xətti qruplar adlanan verilmiş ölçülü tərsi olan bütün matrislərin qruplarıdır. Matrislərin hasilləri və tərsləri altında qorunan matrislərin istənilən xassəsindən sonrakı matris qruplarını təyin etmək üçün istifadə edilə bilər. Məsələn, verilmiş ölçülü, determinantı 1 olan matrislər, xüsusi xətti qrup adlanan ümumi xətti qrupun (yəni daxilində olan daha kiçik bir qrupun) altqrupunu təşkil edir. Aşağıdakı

M^TM = I

şərti ilə təyin olunan ortoqonal matrislər ortoqonal qrup təşkil edir. Hər bir ortoqonal matrisin determinantı 1 və ya −1 olur. Determinantı 1 olan ortoqonal matrislər xüsusi ortoqonal qrup adlanan altqrupu təşkil edir. Simmetrik qrupun nizamlı təsvirini nəzərə almaqla görmək olar ki, hər bir sonlu qrup matris qrupuna izomorfdur. Ümumi qruplar təqdimat nəzəriyyəsi vasitəsilə nisbətən yaxşı başa düşülən matris qruplarından istifadə etməklə öyrənilə bilər.

Sonsuz matrislər

Sonsuz sayda sətir və/və ya sütuna malik matrislər, sonsuz obyektlərdən ibarət olmalarına baxmayaraq, aşkar formada yazılmadan da düşünülə bilərlər. Əhəmiyyətli olan odur ki, çoxluq indeksləşdirmə sətirlərindəki hər bir element və çoxluq indeksləşdirmə sütunlarındakı hər bir element üçün yaxşı müəyyən edilmiş bir giriş var (hətta bu indeks çoxluqlarının natural ədədlərin alt çoxluqları olmasına ehtiyac yoxdur). Toplama, çıxma, skalyara vurma və transponirə etmə kimi əsas əməllər hələ də problemsiz şəkildə təyin edilə bilər; lakin matrislərin vurulması nəticədə olan elementləri müəyyən etmək üçün sonsuz cəmləmələri əhatə edə bilər və bunlar ümumiyyətlə təyin olunmamışdır. Əgər R hər hansı vahid halqadırsa, onda düzgün R modulu kimi ${\displaystyle M=\bigoplus _{i\in I}R}$-in endomorfizm halqası elementləri ${\displaystyle I\times I}$ ilə indekslənən ${\displaystyle \mathrm {CFM} _{I}(R)}$ sonlu sütunlu matrislər halqasına izomorfdur və sütunların hər biri yalnız sonlu sayda sıfırdan fərqli elementlərdən ibarətdir. Sol R modulu kimi qəbul edilən M-in endomorfizmləri analoji obyektlə, sətirlərinin hər biri yalnız sonlu sayda sıfırdan fərqli elementlərdən ibarət olan sonlu sətirli ${\displaystyle \mathrm {RFM} _{I}(R)}$ matrisləri ilə nəticələnir.

Xətti çevirmələri təsvir etmək üçün sonsuz matrislərdən istifadə edilirsə, aşağıdakı səbəbə görə yalnız sütunları sonlu sayda sıfırdan fərqli elementlərdən ibarət bütün matrislər istifadə edilə bilər. A matrisinin xətti f: V→W çevirməsini təsvir etməsi üçün, hər iki fəza üçün bazislər seçilmiş olmalıdır; (xatırlamaq lazımıdır ki, tərifə görə bu o deməkdir ki, fəzadakı hər bir vektor yeganə şəkildə bazis vektorların (sonlu) xətti kombinasiyası kimi ifadə edilə bilər), beləliklə, əmsalların (sütun) v vektoru kimi yazılan zaman yalnız sonlu sayda v_i elementləri sıfırdan fərqli olur. İndi A sütunları W əsasında V-nin fərdi bazis vektorlarının təsvirlərini f ilə təsvir edir, bu, yalnız bu sütunların yalnız sonlu sayda sıfırdan fərqli elementlərə malik olduğu halda məna kəsb edir. Bununla belə, A-nın sətirlərində heç bir məhdudiyyət yoxdur: A·v hasilində yalnız v-nin sonlu sayda sıfırdan fərqli əmsalları iştirak edir, ona görə də onun hər bir elementi, hətta hasilin sonsuz cəmi kimi verilsə belə, yalnız sonlu sayda sıfırdan fərqli hədlərə malik olur və buna görə də yaxşı təyin olunmuşdur. Üstəlik, bu, A sütunlarının yalnız sonlu bir küllüsünü təsirli şəkildə əhatə edən xətti kombinasiyasının formalaşdırılmasına ekvivalentdir, beləliklə, nəticədə yalnız sonlu sayda sıfırdan fərqli elementlər olur, çünki bu sütunların hər biri bunu edir. Verilmiş tipli iki matrisin hasili yaxşı təyin edilib (sütun-indeks və sətir-indeks çoxluqları uyğun gəlmək şərti ilə), eyni tiplidir və xətti çevirmələrin kompozisiyasına uyğundur.

Əgər R normalaşdırılmış halqadırsa, o zaman sətir və ya sütunun sonluluğu şərti yumşaldıla bilər. Norma yerində olduqda, sonlu cəmlərin əvəzinə mütləq yaxınlaşan sıralardan istifadə edilə bilər. Məsələn, sütunları cəmləri mütləq yaxınlaşan ardıcıllıq olan matrislər halqa əmələ gətirir. Analoji olaraq, sətirləri cəmi mütləq yaxınlaşan sıra olan matrislər də halqa əmələ gətirir. Sonsuz matrislər yaxınlaşma və kəsilməzlik problemlərinin meydana gəldiyi və yenə tətbiq ediməli olan müəyyən məhdudiyyətlərlə nəticələnən Hilbert fəzalarındakı operatorları ifadə etmək üçün də istifadə edilə bilər. Bununla belə, matrislərin açıq-aydın nöqteyi-nəzəri məsələni çaşdırmağa meyillidir və bunun əvəzinə mücərrəd və daha güclü funksional analiz vasitələrindən istifadə edilə bilər.

Boş matris

Sətir və ya sütunlarının (və ya hər ikisinin) sayı sıfır olan matris boş matris adlanır.

Boş matrislər sıfır vektor fəzasını əhatə edən çevirmələrlə işləməyə kömək edir. Məsələn, A 3x0 ölçülü matris, B isə 0x3 ölçülü matrisdirsə, AB 3-ölçülü V fəzasından özünə doğru olan sıfır çevirməyə uyğun gələn 3x3 ölçlü sıfır matris, BA isə 0-a 0 matrisidir. Boş matrislər üçün ümumi işarələmə yoxdur, lakin əksər kompüter cəbr sistemləri onları yaratmağa və hesablamalar aparmağa imkan verir. 0x0 ölçülü matrisin determinantı, determinant üçün Leybnits düsturunda meydana gələn boş hasillə əlaqədar olaraq 1-ə bərabərdir. Bu qiymət həm də hər hansı sonlu ölçülü fəzadan özünə doğru olan eynilik çevirməsinin 1 determinantına malik olması faktına uyğundur, bu fakt çox vaxt determinantların xarakteristikasının bir hissəsi kimi istifadə olunur.

Tətbiqlər

Matrislərin həm riyaziyyatda, həm də digər elmlərdə çoxsaylı tətbiqləri var. Bəzən onlardan sadəcə olaraq ədədlər yığımını yığcam formada təsvir etmək üçün istifadə edirlər. Məsələn, oyunlar nəzəriyyəsi və iqtisadiyyatda qazanc matrisi, oyunçuların verilmiş (sonlu) alternativlər çoxluğundan hansını seçməsindən asılı olaraq iki oyunçuya uyğun gələn qazancı özündə əks etdirir. Mətnin öyrənilməsi və avtomatlaşdırılmış tezaurus tərtibi bir neçə sənəddə müəyyən sözlərin tezliyini izləmək üçün tf-idf kimi sənəd-söz matrislərindən istifadə edir.

Kompleks ədədlər 2x2 ölçülü məxsusi həqiqi

${\displaystyle a+ib\leftrightarrow {\begin{bmatrix}a&-b\\b&a\end{bmatrix}},}$

matrisləriylə göstərilə bilər ki, bu halda da kompleks ədədlərin və matrislərin toplanması və vurulması bir-birinə uyğun gəlir. Məsələn, 2x2 ölçülü dönmə matrisləri yuxarıda göstərildiyi kimi kompleks ədədin mütləq qiyməti olan 1-ə vurmanı ifadə edir. Oxşar izahı kvaternionlara və ümumilikdə Klifford cəbrlərinə də şamil etmək olar.

Hill şifri kimi qədim şifrələmə üsulları da matrislərin tətbiqinə əsaslanırdı. Buna baxmayaraq, matrislərin xətti təbiətinə görə, bu kodları sındırmaq nisbətən asandır.Kompüter qrafikası nəzəri kamera müşahidəsinə uyğun olaraq matrislərdən üçölçülü obyektin ikiölçülü ekrana proyeksiyası kimi tapşırıqları yerinə yetirmək üçün həm obyektləri göstərmək, həm də affin fırlanma matrislərindən istifadə edərək obyektlərin çevrilməsini hesablamaq üçün istifadə edir. Çoxhədli halqası üzərindəki matrislər idarəetmə nəzəriyyəsinin öyrənilməsində mühüm əhəmiyyət kəsb edir.

Kimyada matrislər müxtəlif məsələlərdə, xüsusən də molekulyar rabitə və spektroskopiyanı öyrənmək üçün kvant nəzəriyyəsinin tətbiq edilməsindən etibarən istifadə olunmaqdadır. Nümunə kimi, Hartri-Fok metodunun molekulyar orbitallarını əldə etmək üçün Rutaan tənliklərinin həllində istifadə olunan uzlaşma və Fok matrisini göstərmək olar.

Qraf nəzəriyyəsi

Qonşuluq matrisi

$${\displaystyle {\begin{bmatrix}1&1&0\\1&0&1\\0&1&0\end{bmatrix}}}$$

şəklində olan istiqamətsiz qraf

Sonlu qrafın qonşuluq matrisi qraf nəzəriyyəsinin əsas anlayışıdır. O qrafın hansı təpələrinin kənarla birləşdirildiyini ifadə edir. Yalnız iki müxtəlif qiyməti olan matrislər (1 və 0, məsələn, müvafiq olaraq "hə" və "yox" mənasında) məntiqi matrislər adlanır. Məsafə (və ya xərc) matrisi kənarların uzunluğu haqqında məlumatları ehtiva edir. Bu anlayışlar hiperlinklərə bağlanan vebsaytlara və ya yollar və s. ilə əlaqələnən şəhərlərə tətbiq oluna bilər, bu halda (əlaqə şəbəkəsi son dərəcə sıx olmadıqda) matrislər seyrək olur, yəni sıfırdan fərqli bir neçə elementə malik olur. Buna görə də, şəbəkə nəzəriyyəsində xüsusi olaraq uyğunlaşdırılmış matris alqoritmlərindən istifadə edilə bilər.

Analiz və həndəsə

Diferensiallanan ƒ: Rⁿ → R funksiyasının Hesse matrisi (Hessianı) ƒ-in bir neçə koordinatına görə ikinci tərtib törəmələrindən ibarətdir, yəni,

${\displaystyle H(f)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}\right].}$

f(x,−y) = x² − y² funksiyasının yəhər nöqtəsində (x = 0, y = 0) (qırmızı) ${\displaystyle {\begin{bmatrix}2&0\\0&-2\end{bmatrix}}}$ Hesse matrisi qeyri-müəyyəndir

O, funksiyanın lokal artım xarakterini təsvir edir: x = (x₁, …, x_n) böhran nöqtəsi, yəni ƒ-in ${\displaystyle \partial f/\partial x_{i}}$ birinci tərtib xüsusi törəmələrinin sıfıra çevrildiyi nöqtə verildikdə, funksiya lokal minimuma malik olur. Matrislərə əlavə olunanlarla sıx əlaqəli olan kvadratik funksiyaların qlobal minimum və ya maksimumlarını tapmaq üçün kvadratik proqramlaşdırmadan istifadə etmək olar (yuxarıya baxın).

Həndəsi situasiyalarda çox zaman istifadə olunan digər matris diferensiallanan f inikasının Yakobi matrisidir: Rⁿ → R^m. Əgər f₁, …, f_m f-in komponentlərini göstərirsə, Yakobi matrisi (Yakobian) bu cür təyin olunur:

${\displaystyle J(f)=\left[{\frac {\partial f_{i}}{\partial x_{j}}}\right]_{1\leq i\leq m,1\leq j\leq n}.}$

Əgər n>m və Yakobi matrisinin ranqı maksimum m qiymətinə çatarsa, qeyri-aşkar funksiya teoreminə görə həmin nöqtədə f lokal tərslənəndir.

Xüsusi törəməli diferensial tənlikləri tənliyin yüksək tərtibli diferensial operatorların əmsallar matrisini nəzərə almaqla təsnif etmək olar. Elliptik xüsusi törəməli diferensial tənliklər üçün bu matris müsbət müəyyəndir və sözügedən tənliyin mümkün həllər çoxluğuna həlledici təsir göstərir.

Sonlu elementlər üsulu mürəkkəb fiziki sistemlərin simulyasiyasında geniş tətbiq olunan xüsusi törəməli diferensial tənliklərin həlli üçün mühüm bir ədədi üsuldur. O bəzi tənlikləri hissə-hissə xətti funksiyalar vasitəsilə yaxınlaşmaqla həll etməyə imkan verir, burada parçalar kifayət qədər incə bir şəbəkə üçün seçilir və bu da öz növbəsində matris tənliyi kimi yenidən tərtib edilə bilər.

Ehtimal nəzəriyyəsi və statistika

İki müxtəlif Markov zənciri. Diaqram "2" vəziyyətində hissəciklərin sayını (cəmi 1000) təsvir edir. Hər iki məhdudlaşdırıcı qiymət ${\displaystyle {\begin{bmatrix}0.7&0\\0.3&1\end{bmatrix}}}$(qırmızı) və ${\displaystyle {\begin{bmatrix}0.7&0.2\\0.3&0.8\end{bmatrix}}}$(qara) tərəfindən verilən keçid matrislərindən müəyyən edilə bilər

Stoxastik matrislər sətirləri ehtimal vektorları olan, yəni elementləri mənfi olmayan və cəmi vahidə bərabər olan kvadrat matrislərdir. Stoxastik matrislər sonlu sayda hala malik Markov zəncirlərini təyin etmək üçün istifadə olunur. Stoxastik matrisin bir sətiri, cari cərgəyə uyğun gələn haldakı bəzi hissəciklərin növbəti mövqeyi üçün ehtimal paylanmasını verir. Markov zəncirinəbənzər udma hallarının xassələri, yəni hər hansı bir hissəciyin son nəticədə çatdığı hallar keçid matrislərinin məxsusi vektorlarından anlaşıla bilər.

Statistikada matrislər müxtəlif formalarda tətbiq edilir. Təsviri statistika çox vaxt verilən (data) matrisləri kimi təqdim oluna bilən və sonra ölçüləri azaltma üsullarına məruz qala bilən verilən çoxluqlarının təsviri ilə əlaqədardır. Kovariasiya matrisi bir neçə təsadüfi dəyişənin qarşılıqlı dispersiyasını kodlaşdırır. Matrislərdən istifadə edən başqa bir üsul xətti ən kiçik kvadratlardır, bu üsulda

y_i ≈ ax_i + b, i = 1, …, N

xətti funksiyasının köməyilə (x₁, y₁), (x₂, y₂), …, (x_N, y_N) sonlu cütlər çoxluğuna yaxınlaşılır. Bu matrislər baxımından tərtib edilə bilir və matrislərin sinqulyar dekompozisiyası ilə əlaqədardır.

Təsadüfi matrislər, elementləri təsadüfi ədədlər olan və matris normal paylanması kimi ehtimal paylanmalarına tabe olan matrislərdir. Ehtimal nəzəriyyəsindən başqa, onlar ədədlər nəzəriyyəsindən tutmuş fizikaya qədər müxtəlif sahələrdə tətbiq olunur.

Fizikada simmetriya və çevirmələr

Xətti çevirmələr və onlarla əlaqəli simmetriyalar müasir fizikada vacib rol oynayır. Məsələn, kvant sahə nəzəriyyəsindəki elementar hissəciklər xüsusi nisbilik nəzəriyyəsinin Lorens qrupunun təsvirləri kimi və daha dəqiq desək, spin qrupu altındakı davranışlarına görə təsnif edilir. Pauli matrislərini və daha ümumi qamma matrislərini əhatə edən konkret təsvirlər spinor kimi davranan fermionların fiziki xarakteristikasının əsas tərkib hissəsidir. Üç ən yüngül kvark üçün SU(3) xüsusi unitar qrupunu əhatə edən qrup-nəzəri təsvir var; fiziklər öz hesablamaları üçün Gell-Mann matrisləri kimi tanınan rahat matris təsvirindən istifadə edirlər ki, bu da güclü nüvə qarşılıqlı təsirlərinin müasir təsvirinin, kvant xromodinamikasının əsasını təşkil edən SU(3) ölçü qrupu üçün də istifadə olunur. Kabibbo-Kobayaşi-Maskava matrisi, öz növbəsində ifadə edir ki, zəif qarşılıqlı təsirlər üçün vacib olan əsas kvark halları konkret və müxtəlif kütləli hissəcikləri təyin edən əsas kvark halları ilə eyni olmayıb, xətti əlaqəlidir.

Kvant hallarının xətti kombinasiyaları

Kvant mexanikasının ilk modeli (Hayzenberq, 1925) nəzəriyyənin operatorlarını kvant hallarına təsir edən sonsuz ölçülü matrislərlə ifadə edirdi. Bu, eyni zamanda matris mexanikası da adlanır. Xüsusi nümunələrdən biri, kvant sisteminin "qarışıq" halını elementar, "xalis" məxsusi halların xətti kombinasiyası kimi xarakterizə edən sıxlıq matrisidir.

Başqa bir halda matris eksperimental hissəciklər fizikasının təməl daşı olan səpilmə təcrübələrini təsvir etmək üçün əsas alət rolunu oynayır: toqquşma reaksiyaları, məsələn, hissəcik sürətləndiricilərində, qarşılıqlı təsir göstərməyən hissəciklərin bir-birinə doğru yönəldiyi və kiçik bir qarşılıqlı təsir zonasında toqquşduğu, yeni nəticədə qarşılıqlı təsir göstərməyən hissəciklər dəsti, çıxan hissəcik vəziyyətlərinin skalyar hasili və daxil olan hissəcik vəziyyətlərinin xətti kombinasiyası kimi təsvir edilə bilər. Xətti kombinasiya hissəciklər arasındakı mümkün qarşılıqlı təsirlər barədə bütün məlumatları özündə saxlayan S-matrislə verilir.

Normal modlar

Matrislərin fizikadakı ümumi tətbiqi xətti əlaqəli harmonik sistemlərin təsviriylə də bağlıdır.

Belə sistemlərin hərəkət tənliklərini matris formasında təsvir etmək üçün kütlə matrisini ümumiləşmiş sürətə (kinetik ifadəni almaq üçün), qüvvə matrisini isə yerdəyişmə vektoruna vurmaq (qarşılıqlı təsirləri xarakterizə etmək üçün) lazımdır. Həlləri əldə etməyin ən yaxşı yolu matris tənliyini diaqonallaşdırmaqla sistemin məxsusi vektorlarını, onun normal modlarını təyin etməkdir. Bu kimi üsullar molekulların daxili dinamikası: bir-birilə əlaqələnmiş komponent atomlarından ibarət sistemlərin daxili rəqsləriylə bağlı mühüm əhəmiyyət kəsb edir. Həmçinin onlar mexaniki rəqsləri və elektrik rəqslərini təsvir etmək üçün lazımdır.

Həndəsi optika

Həndəsi optika matrislərin tətbiqi üçün daha çox imkan yaradır. Bu yaxınlaşma nəzəriyyəsində işığın dalğa təbiəti nəzərə alınmır. Nəticədə, işıq şüalarının həqiqətən də həndəsi şüalar olduğu model alınır. Əgər işıq şüalarının optik elementlər tərəfindən meyllənməsi kiçikdirsə, linza və ya qaytarıcı elementin verilmiş işıq şüasına təsiri ikikomponentli vektorun şüa ötürmə matris analizi adlanan 2x2 ölçülü matrislə vurulması kimi ifadə edilə bilər: vektorun komponentləri işıq şüasının mailliyi və optik oxdan uzaqlığıdır, matris isə optik elementin xassələrini kodlaşdırır. Faktiki olaraq, iki növ matris var, yəni linza səthində sınmanı təsvir edən sınma matrisi və istinad müstəvisinin başqa bir sınma matrisinin tətbiq olunduğu növbəti sındırıcı səthə ötürülməsini təsvir edən ötürmə matrisi. Linza və/və ya qaytarıcı elementlərin birləşməsindən ibarət olan optik sistem sadə formada komponentlərin matrislərinin hasili nəticəsində yaranan matrislə təsvir edilir.

Elektronika

Elektronikadakı ənənəvi kontur cərəyanları və potensiallar metodu matrislə təsvir edilə bilən xətti tənliklər sisteminə gətirib çıxarır. Bir çox elektron komponentlərin davranışı matrislərin köməyilə təsvir edilə bilər. A elementləri komponentin v₁ giriş gərginliyi və i₁ giriş cərəyanından ibarət 2-ölçülü vektor, B isə elementləri komponentin v₂ çıxış gərginliyi və i₂ çıxış cərəyanından ibarət 2-ölçülü vektor olsun. Sonra elektron komponentin davranışı B = H · A ilə təsvir edilə bilər, burada H bir impedans (h₁₂), bir admittans (h₂₁) elementindən və iki ədəd ölçüsüz elementdən (h₁₁ və h₂₂) ibarət 2 x 2 ölçülü matrisdir. Sonda dövrənin hesabatı matrislərin vurulmasına gətirilir.

Tarix

Matrislər xətti tənliklərin həllində tətbiq olunma ilə bağlı uzunmüddətli keçmişə sahibdir, lakin onlar 1800-cü illərə qədər nizamlı elementlər yığımı (massiv) kimi tanınırdılar. Eramızdan əvvəl 10–2-ci əsrlərdə yazılmış Çin mətni olan Riyazi sənətə dair doqquz fəsil tənliklər sisteminin həlli üçün massiv metodlarından, o cümlədən determinant anlayışından istifadənin ilk nümunəsidir. 1545-ci ildə italyan riyaziyyatçısı Cerolamo Kardano, Ars Magna (Dahiyanə incəsənət) kitabını nəşr etdirərkən bu metodu Avropaya təqdim etdi. 1683-cü ildə yapon riyaziyyatçısı Seki tənliklər sistemini həll etmək üçün eyni massiv üsullarından istifadə etdi. Niderland riyaziyyatçısı Jan de Vitt 1659-cu ildə çap olunmuş Əyrilərin elementləri (1659) kitabında massivlərdən istifadə edərək çevirmələri göstərmişdir. 1700–1710-cu illər arasında Qotfrid Vilhelm Leybnits informasiya və ya həlləri qeyd etmək üçün massivlərin istifadəsini açıqladı və 50-dən artıq müxtəlif massivlər sistemini təcrübədən keçirdi. 1750-ci ildə Kramer öz qaydasını təqdim etdi.

"Matris" termini (latınca "bətn, başlanğıc" mənasını verən mater—ana sözündən törəmişdir) 1850-ci ildə Ceyms Cozef Silvestr tərəfindən istifadə edilmişdir, o, matrisi bu gün minorlar adlanan bir neçə determinantın, yəni, sütun və sətirləri silməklə orijinaldan əldə edilən kiçik matrislərin determinantlarının yaranmasına səbəb olan obyekt kimi başa düşür. 1851-ci ildə bir məqaləsində Silvestr bunu belə izah edir:

Əvvəlki məqalələrdə mən "Matris"i ümumi bir valideynin bətnində olduğu kimi müxtəlif determinant sistemlərinin yaradıla biləcəyi düzbucaqlı ifadələr yığımı kimi təyin etmişdim.

Artur Keli əvvəllər edildiyi kimi tədqiq edilən əmsalların dönmə variantları olmayan matrislərdən istifadə edərək həndəsi çevrirmələr haqqındakı traktatını nəşr etdirdi. Bunun əvəzinə o, toplama, çıxma, vurma və bölmə kimi əməlləri həmin matrislərin çevrilmələri kimi təyin etdi və assosiativ və distributivlik kimi dəyişməz xassələri ifadə etdi. Keli matrislərin vurulmasının qeyri-kommutativ xassəsini, eləcə də matrisin toplanmasının kommutativ xassəsini tədqiq etdi və göstərdi. Əvvəllər matris nəzəriyyəsi massivlərin istifadəsini demək olar ki, yalnız determinantlarla məhdudlaşdırmışdı və Artur Kelinin mücərrəd matris əməlləri inqilabi idi. O, tənlik sistemlərindən asılı olmayan matris konsepsiyasının təklif edilməsində mühüm rol oynamışdır. 1858-ci ildə Keli, Keli-Hamilton teoremini təklif etdiyi və göstərdiyi Matrislər nəzəriyyəsiylə bağlı xatirələrini nəşr etdirdi.

İngilis riyaziyyatçısı Katbert Edmund Kullis 1913-cü ildə matrislər üçün bugünkü düzbucaqlı mötərizə işarələrini istifadə edən ilk şəxsdir və eyni zamanda o, matrisi ifadə etmək üçün A = [a_{i, j}] işarələməsinin ilk əhəmiyyətli istifadəsini nümayiş etdirmişdir (burada a_{i, j} i-ci sıra və j-ci sütunu nəzərdə tutur).

Determinantların müasir tədqiqi bir neçə mənbədən qaynaqlanır. Ədədlər nəzəriyyəsinə dair məsələlər Qaussu kvadratik formaların, yəni x² + xy − 2y² kimi ifadələrin əmsallarını və üçölçülü xətti çevirmələri matrislərlə əlaqələndirməyə vadar etdi. Eyzenşteyn müasir dillə desək, matrislər hasilinin qeyri-kommutativ olduğunu söyləməklə birlikdə bu anlayışları daha da inkişaf etdirdi. Koşi A = [a_{i, j}] matrisinin determinantının tərifi kimi aşağıdakılardan istifadə edərək, aşağıdakı çoxhədlidə a_j^k qüvvətlərini a_jk ilə əvəz etməklə determinantlar haqqındakı ümumi müddəaları ilk dəfə olaraq isbat etdi

${\displaystyle a_{1}a_{2}\cdots a_{n}\prod _{i<j}(a_{j}-a_{i})\;}$

burada Π göstərilən hədlərin hasilini bildirir. O, həmçinin 1829-cu ildə simmetrik matrislərin məxsusi qiymətlərinin həqiqi olduğunu da göstərdi. Yakobi lokal (və ya sonsuz kiçik) səviyyədə həndəsi çevirmələri təsvir etmək üçün istifadə edilən "funksional determinantları" (sonralar Silvestr tərəfindən Yakobi determinantları adlandırılmışdır) araşdırdı (yuxarıya baxın); Kronekerin Vorlesungen über die Theorie der Determinanten (Determinantlar nəzəriyyəsi üzrə mühazirələr) və hər ikisi 1903-cü ildə nəşr olunan Veyerştrassın Zur Determinantentheorie (Determinantlar nəzəriyyəsinə) əsərlərində Koşinin qeyd olunan düsturu kimi əvvəlki daha konkret yanaşmalardan fərqli olaraq, ilk dəfə determinantları aksiomatik şəkildə nəzərdən keçirdi. Bu nöqtədə determinantlar ciddi şəkildə qurulmuşdu.

Bir çox teoremlər ilk dəfə yalnız yığcam matrislər üçün yaradılmışdır, məsələn, Keli-Hamilton teoremi yuxarıda qeyd olunan memuarda Keli tərəfindən 2×2 ölçülü matrislər üçün, Hamilton tərəfindən isə 4×4 matrislər üçün isbat edilmişdir. Bixətti formalar üzərində işləyən Forbenius, teoremi bütün ölçülər üçün ümumiləşdirdi (1898). Həmçinin 19-cu əsrin sonlarında Vilhelm Jordan tərəfindən Qauss-Jordan üsulu (indi Qauss üsulu adlanan xüsusi halın ümumiləşməsi) yaradıldı. 20-ci əsrin əvvəllərində matrislər, qismən əvvəlki əsrin hiperkompleks ədəd sistemlərinin təsnifatında istifadə edildiyinə görə xətti cəbrdə mərkəzi rola sahib oldular.

Hayzenberq, Born və Jordan tərəfindən matris mexanikasının yaradılması sonsuz sayda sətir və sütundan ibarət matrislərin öyrənilməsinə səbəb oldu. Daha sonra fon Neyman Hilbert fəzaları üzərindəki xətti operatorlar kimi funksional analitik anlayışları daha da inkişaf etdirərək kvant mexanikasının riyazi formulyasiyasını həyata keçirdi; bunlar, kobud şəkildə desək, Evklid fəzasına uyğun gəlir, lakin sonsuz sayda sərbəst istiqamətə malikdir.

Riyaziyyatda "matris" sözünün digər tarixi istifadələri

Bu söz ən azından tarixi önəmə malik iki müəllif tərəfindən qeyri-adi şəkildə istifadə edilmişdir.

Bertran Rassel və Alfred Nort Vaythed Principia Mathematica (Riyaziyyatın əsasları) (1910–1913) əsərində "matris" sözünü sadələşdiriləbilmə aksiomları kontekstində istifadə edirlər.

Onlar bu aksiomu hər hansı funksiyanı ardıcıl olaraq daha aşağı növdən birinə sadələşdirmə vasitəsi kimi təklif etdilər, beləliklə də, "aşağıdakı" (0 sıra) funksiya onun artımı ilə eyniləşdirildi:

"Gəlin dəyişənlərin sayı nə qədər çox olsa da, heç bir zahiri dəyişənləri ehtiva etməyən istənilən funksiyaya matrisin adını verək. Bu zaman matris istisna olmaqla başqa hər hansı mümkün funksiya ümumiləşdirmə yolu ilə, yəni təklifi nəzərə almaqla matrisdən alınır və bu sözügedən funksiyanın bütün mümkün qiymətlərlə və ya arqumentlərdən birinin bəzi qiymətləri üçün, digər arqument və ya arqumentlər qeyri-müəyyən olduqda doğrudur".

Məsələn, x və y dəyişənlərinin Φ(x, y) funksiyası "obyektlərin" bütün mümkün qiymətləri üçün funksiyanı nəzərə alaraq bir dəyişənli funksiyalar yığımına gətirilə bilər. Və sonra ortaya çıxan birdəyişənli funksiyalarının yığımı, yəni ∀a_i: Φ(a_i, y), y dəyişəninin yerinə yazılan b_i "obyektlərinin" bütün mümkün qiymətləri üçün funksiya "nəzərə alınmaqla" qiymətlər "matrisinə" gətirilə bilər:

∀b_j∀a_i: Φ(a_i, b_j).

Alfred Tarski 1946-cı ildə Məntiqə giriş əsərində "matris" sözünü riyazi məntiqdə istifadə edilən doğruluq cədvəli anlayışının sinonimi kimi işlətmişdir.

Qeydlər

1. Bununla belə, qonşuluq matrisləri halında, matrislərin vurulması və ya onun bir variantı eyni vaxtda istənilən iki təpə arasındakı yollar sayını və iki təpə arasındakı ən qısa məsafəni hesablamağa imkan verir.
2. Lang, 2002
3. Fraleigh, (1976. səh. 209)
4. Nering, 1970. səh. 37
5. Weisstein, Eric W. "Matrix". mathworld.wolfram.com (ingilis). 2022-09-12 tarixində . İstifadə tarixi: 2020-08-19.
6. Oualline, 2003, Fəsil 5
7. Pop; Furdui (2017). Square Matrices of Order 2. Springer International Publishing. ISBN .
8. "Matrisləri necə təşkil etmək, toplamaq və vurmaq olar – Bill Shillito". TED ED. April 10, 2022 tarixində . İstifadə tarixi: April 6, 2013.
9. Brown, 1991, Tərif I.2.1 (toplama), Tərif I.2.4 (skalyara vurma), və Tərif I.2.33 (transponirə etmə)
10. Brown, 1991, Teorem I.2.6
11. "How to Multiply Matrices". www.mathsisfun.com. 2022-08-14 tarixində . İstifadə tarixi: 2020-08-19.
12. Brown, 1991, Tərif I.2.20
13. Brown, 1991, Teorem I.2.24
14. Horn, Johnson, 1985. səh. 4 və 5
15. Bronson, (1970. səh. 16)
16. Kreyszig, (1972. səh. 220)
17. Protter, Morrey, (1970. səh. 869)
18. Kreyszig, (1972. səh. 241,244)
19. Schneider, Hans; Barker, George Phillip, Matrices and Linear Algebra, Dover Books on Mathematics, Courier Dover Corporation, 2012, səh. 251, ISBN , 2022-04-10 tarixində , İstifadə tarixi: 2022-05-24.
20. Perlis, Sam, Theory of Matrices, Dover books on advanced mathematics, Courier Dover Corporation, 1991, səh. 103, ISBN , 2022-04-10 tarixində , İstifadə tarixi: 2022-05-24.
21. Anton, Howard, Elementary Linear Algebra (10th), John Wiley & Sons, 2010, səh. 414, ISBN , 2022-04-10 tarixində , İstifadə tarixi: 2022-05-24.
22. Horn, Roger A.; Johnson, Charles R., Matrix Analysis (2nd), Cambridge University Press, 2012, səh. 17, ISBN , 2022-04-10 tarixində , İstifadə tarixi: 2022-05-24.
23. Brown, 1991, I.2.21 və 22
24. Greub 1975. səh. Bölmə III.2
25. Brown, 1991, Tərif II.3.3
26. Greub 1975, Bölmə III.1
27. Brown, 1991, Teorem II.3.22
28. Horn, Johnson, 1985, Teorem 2.5.6
29. Brown, 1991, Tərif I.2.28
30. Brown, 1991, Tərif I.5.13
31. Horn, Johnson, 1985, Fəsil 7
32. Horn, Johnson, 1985, Teorem 7.2.1
33. Horn, Johnson, 1985, Nümunə 4.0.6, səh. 169
34. "Matrix | mathematics". Encyclopedia Britannica (ingilis). 2022-08-14 tarixində . İstifadə tarixi: 2020-08-19.
35. Brown, 1991, Tərif III.2.1
36. Brown, 1991, Teorem III.2.12
37. Brown, 1991, Nəticə III.2.16
38. Mirsky 1990, Teorem 1.4.1
39. Brown, 1991, Teorem III.3.18
40. Brown, 1991, Tərif III.4.1
41. Brown, 1991, Tərif III.4.9
42. Brown, 1991, Nəticə III.4.10
43. Householder, 1975, Fəsil 7
44. Bau III & Trefethen 1997
45. Golu, Van Loan, 1996, Alqoritm 1.3.1
46. Golub, Van Loan, 1996, Fəsil 9 və 10, xüs. bölmə 10.2
47. Golub, Van Loan, 1996, Fəsil 2.3
48. Grcar, Joseph F. "John von Neumann's Analysis of Gaussian Elimination and the Origins of Modern Numerical Analysis". SIAM Review. 53 (4). 2011-01-01: 607–682. doi:10.1137/080734716. ISSN 0036-1445. 2022-08-27 tarixində . İstifadə tarixi: 2022-05-25.
49. Məsələn, Mathematica, bax Wolfram, 2003, Fəsil 3.7
50. Press və b. 1992
51. Stoer, Bulirsch, 2002, Bölmə 4.1
52. Horn, Johnson, 1985, Teorem 2.5.4
53. Arnold və b.
54. Bronson, 1989, Fəsil 15
55. Coburn, 1955, Fəsil V
56. Lang, 2002, Fəsil XIII
57. Lang, 2002, XVII.1, p. 643
58. Lang, 2002, Təklif XIII.4.16
59. Reichl, 2004, Bölmə L.2
60. Greub, 1975, Bölmə III.3
61. Greub, 1975, Bölmə III.3.13
62. Qrupdakı hər hansı bir standart istinada baxın.
63. Əlavə olaraq, qrup ümumi xətti qrupda qapalı olmalıdır.
64. Baker, 2003, Tərif 1.30
65. Baker, 2003, Teorem 1.2
66. Artin, 1991, Fəsil 4.5
67. Rowen, 2008, Nümunə 19.2, səh. 198
68. Təqdimat nəzəriyyəsi və ya qrup təqdimatına dair hər hansı bir istinada baxın.
69. Itõ (1987)-da "Matrix" maddəsinə baxın
70. "Matris nəzəriyyəsinin çoxu sonsuz ölçülü fəzalara keçmir və bu o qədər də faydalı deyil, lakin bəzən kömək edir." Halmos, 1982, səh. 23, 5-ci fəsil
71. "Boş Matris: Sətir və ya sütunlarının ölçüsü sıfırdır olan matris boşdur", Glossary 2009-04-29 at the Wayback Machine, O-Matrix v6 User Guide
72. "Ən azı bir ölçüsü sıfıra bərabər olan matrisə boş matris deyilir", MATLAB Data Structures 2009-12-28 at the Wayback Machine
73. Fudenberg, Tirole, 1983, Bölmə 1.1.1
74. Ward, 1997, Fəsil 2.8
75. Stinson, 2005, Fəsil 1.1.5 və 1.2.4
76. Association for Computing Machinery, 1979, Fəsil 7
77. Godsil, Royle, 2004, Fəsil 8.1
78. Punnen, 2002
79. Lang, 1987a, Fəsil XVI.6
80. Nocedal, 2006, Fəsil 16
81. Lang, 1987a, Fəsil XVI.1
82. Lang, 1987a, Fəsil XVI.5. Daha təkmil və ümumi izahat üçün bax: Lang, 1969, Fəsil VI.2
83. Gilbarg, Trudinger, 2001
84. Šolin, 2005, Fəsil 2.5.
85. Latouche, Ramaswami, 1999
86. Mehata, Srinivasan, 1978, Fəsil 2.8
87. Krzanowski, 1988. səh. 60, Fəsil 2.2.
88. Krzanowski, 1988, Fəsil 4.1
89. Itzykson, Zuber, 1980, Fəsil 2
90. bax: Burgess, Moore, 2007, bölmə 1.6.3. (SU(3)), bölmə 2.4.3.2. (Kobayashi–Maskawa matrix)
91. Schiff, 1968, Fəsil 6
92. Bohm, 2001, bölmə II.4 və II.8
93. Weinberg, 1995, Fəsil 3
94. Wherrett, 1987, II hissə
95. Riley, Hobson və Bence, 1997, 7.17
96. Guenther, 1990, Fəsil 5
97. Shen, Crossley və Lun, 1999 ilə yanaşı Bretscher, 2005. səh. 1
98. Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Published by Addison Wesley, October 10, 2001 ISBN , p. 564–565
99. Needham, Joseph; Wang Ling. Science and Civilisation in China. III. Cambridge: Cambridge University Press. 1959. səh. 117. ISBN . 2022-05-26 tarixində . İstifadə tarixi: 2022-05-26.
100. Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Published by Addison Wesley, October 10, 2001 ISBN , p. 564
101. Merriam-Webster dictionary, Merriam-Webster, August 2, 2022 tarixində , İstifadə tarixi: April 20, 2009
102. Although many sources state that J. J. Sylvester coined the mathematical term "matrix" in 1848, Sylvester published nothing in 1848. (For proof that Sylvester published nothing in 1848, see: J. J. Sylvester with H. F. Baker, ed., The Collected Mathematical Papers of James Joseph Sylvester (Cambridge, England: Cambridge University Press, 1904), vol. 1. 2022-05-26 at the Wayback Machine) His earliest use of the term "matrix" occurs in 1850 in J. J. Sylvester (1850) "Additions to the articles in the September number of this journal, "On a new class of theorems," and on Pascal's theorem," The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 37: 363–370. From page 369 2022-05-26 at the Wayback Machine: "For this purpose, we must commence, not with a square, but with an oblong arrangement of terms consisting, suppose, of m lines and n columns. This does not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants … "
103. The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853, Paper 37 2022-05-26 at the Wayback Machine, p. 247
104. Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Published by Addison Wesley, October 10, 2001 ISBN , p. 564–565
105. Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Published by Addison Wesley, October 10, 2001 ISBN , p. 564–565
106. Phil. Trans. 1858, vol.148, pp.17–37 Math. Papers II 475–496
107. Dieudonné, 1978, Cild 1, Fəsil III, səh. 96
108. Knobloch, 1994
109. Hawkins, 1975
110. Kronecker, 1897
111. Weierstrass, 1915. səh. 271–286
112. Bôcher, 2004
113. Mehra, Rechenberg, 1987
114. Whitehead, Alfred North; and Russell, Bertrand (1913) Principia Mathematica to *56, Cambridge at the University Press, Cambridge UK (republished 1962) cf page 162ff.
115. Tarski, Alfred; (1946) Introduction to Logic and the Methodology of Deductive Sciences, Dover Publications, Inc, New York NY, ISBN .

İstinadlar

• Anton, Howard, Elementary Linear Algebra (5th), New York: Wiley, 1987, ISBN 
• Arnold, Vladimir I.; Cooke, Roger, Ordinary differential equations, Berlin, DE; New York, NY: Springer-Verlag, 1992, ISBN 
• Artin, Michael, Algebra, Prentice Hall, 1991, ISBN 
• Association for Computing Machinery, Computer Graphics, Tata McGraw–Hill, 1979, ISBN 
• Baker, Andrew J., Matrix Groups: An Introduction to Lie Group Theory, Berlin, DE; New York, NY: Springer-Verlag, 2003, ISBN 
• Bau III, David; Trefethen, Lloyd N., Numerical linear algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, 1997, ISBN 
• Beauregard, Raymond A.; Fraleigh, John B., A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., 1973, ISBN 
• Bretscher, Otto, Linear Algebra with Applications (3rd), Prentice Hall, 2005
• Bronson, Richard, Matrix Methods: An Introduction, New York: Academic Press, 1970, LCCN 70097490
• Bronson, Richard, Schaum's outline of theory and problems of matrix operations, New York: McGraw–Hill, 1989, ISBN 
• Brown, William C., Matrices and vector spaces, New York, NY: Marcel Dekker, 1991, ISBN 
• Coburn, Nathaniel, Vector and tensor analysis, New York, NY: Macmillan, 1955, OCLC 1029828
• Conrey, J. Brian, Ranks of elliptic curves and random matrix theory, Cambridge University Press, 2007, ISBN 
• Fraleigh, John B., A First Course In Abstract Algebra (2nd), Reading: Addison-Wesley, 1976, ISBN 
• Fudenberg, Drew; Tirole, Jean, Game Theory, MIT Press, 1983
• Gilbarg, David; Trudinger, Neil S., Elliptic partial differential equations of second order (2nd), Berlin, DE; New York, NY: Springer-Verlag, 2001, ISBN 
• Godsil, Chris; Royle, Gordon, Algebraic Graph Theory, Graduate Texts in Mathematics, 207, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 
• Golub, Gene H.; Van Loan, Charles F., Matrix Computations (3rd), Johns Hopkins, 1996, ISBN 
• Greub, Werner Hildbert, Linear algebra, Graduate Texts in Mathematics, Berlin, DE; New York, NY: Springer-Verlag, 1975, ISBN 
• Halmos, Paul Richard, A Hilbert space problem book, Graduate Texts in Mathematics, 19 (2nd), Berlin, DE; New York, NY: Springer-Verlag, 1982, ISBN ,  0675952
• Horn, Roger A.; Johnson, Charles R., Matrix Analysis, Cambridge University Press, 1985, ISBN 
• Householder, Alston S., The theory of matrices in numerical analysis, New York, NY: Dover Publications, 1975,  0378371
• Kreyszig, Erwin, Advanced Engineering Mathematics (3rd), New York: Wiley, 1972, ISBN .
• Krzanowski, Wojtek J., Principles of multivariate analysis, Oxford Statistical Science Series, 3, The Clarendon Press Oxford University Press, 1988, ISBN ,  0969370
• Itô, Kiyosi, redaktorEncyclopedic dictionary of mathematics. Vol. I-IV (2nd), MIT Press, 1987, ISBN ,  0901762
• Lang, Serge, Analysis II, Addison-Wesley, 1969
• Lang, Serge, Calculus of several variables (3rd), Berlin, DE; New York, NY: Springer-Verlag, 1987a, ISBN 
• Lang, Serge, Linear algebra, Berlin, DE; New York, NY: Springer-Verlag, 1987b, ISBN 
• , Algebra, , 211 (Revised third), New York: Springer-Verlag, 2002, ISBN ,  1878556
• Latouche, Guy; Ramaswami, Vaidyanathan, Introduction to matrix analytic methods in stochastic modeling (1st), Philadelphia, PA: Society for Industrial and Applied Mathematics, 1999, ISBN 
• Manning, Christopher D.; Schütze, Hinrich, Foundations of statistical natural language processing, MIT Press, 1999, ISBN 
• Mehata, K. M.; Srinivasan, S. K., Stochastic processes, New York, NY: McGraw–Hill, 1978, ISBN 
• Mirsky, Leonid, An Introduction to Linear Algebra, Courier Dover Publications, 1990, ISBN 
• Nering, Evar D., Linear Algebra and Matrix Theory (2nd), New York: Wiley, 1970, LCCN 76-91646
• Nocedal, Jorge; Wright, Stephen J., Numerical Optimization (2nd), Berlin, DE; New York, NY: Springer-Verlag, 2006, səh. 449, ISBN 
• Oualline, Steve, Practical C++ programming, O'Reilly, 2003, ISBN 
• Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T., (PDF) // Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd), Cambridge University Press, 1992, 34–42, Archived from the original on 2009-09-06
• Protter, Murray H.; Morrey, Jr., Charles B., College Calculus with Analytic Geometry (2nd), Reading: Addison-Wesley, 1970, LCCN 76087042
• Punnen, Abraham P.; Gutin, Gregory, The traveling salesman problem and its variations, Boston, MA: Kluwer Academic Publishers, 2002, ISBN 
• Reichl, Linda E., The transition to chaos: conservative classical systems and quantum manifestations, Berlin, DE; New York, NY: Springer-Verlag, 2004, ISBN 
• Rowen, Louis Halle, Graduate Algebra: noncommutative view, Providence, RI: American Mathematical Society, 2008, ISBN 
• Šolin, Pavel, Partial Differential Equations and the Finite Element Method, Wiley-Interscience, 2005, ISBN 
• Stinson, Douglas R., Cryptography, Discrete Mathematics and its Applications, Chapman & Hall/CRC, 2005, ISBN 
• Stoer, Josef; Bulirsch, Roland, Introduction to Numerical Analysis (3rd), Berlin, DE; New York, NY: Springer-Verlag, 2002, ISBN 
• Ward, J. P., Quaternions and Cayley numbers, Mathematics and its Applications, 403, Dordrecht, NL: Kluwer Academic Publishers Group, 1997, doi:10.1007/978-94-011-5768-1, ISBN ,  1458894
• Wolfram, Stephen, The Mathematica Book (5th), Champaign, IL: Wolfram Media, 2003, ISBN 

Fizikaya aid istinadlar

• Bohm, Arno, Quantum Mechanics: Foundations and Applications, Springer, 2001, ISBN 
• Burgess, Cliff; Moore, Guy, The Standard Model. A Primer, Cambridge University Press, 2007, ISBN 
• Guenther, Robert D., Modern Optics, John Wiley, 1990, ISBN 
• Itzykson, Claude; Zuber, Jean-Bernard, Quantum Field Theory, McGraw–Hill, 1980, ISBN 
• Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J., Mathematical methods for physics and engineering, Cambridge University Press, 1997, ISBN 
• Schiff, Leonard I., Quantum Mechanics (3rd), McGraw–Hill, 1968
• Weinberg, Steven, The Quantum Theory of Fields. Volume I: Foundations, Cambridge University Press, 1995, ISBN 
• Wherrett, Brian S., Group Theory for Atoms, Molecules and Solids, Prentice–Hall International, 1987, ISBN 
• Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul, Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry), Berlin, DE; New York, NY: Springer-Verlag, 2006, ISBN 

Tarixi istinadlar

• A. Cayley A memoir on the theory of matrices. Phil. Trans. 148 1858 17–37; Math. Papers II 475–496
• Bôcher, Maxime, Introduction to higher algebra, New York, NY: Dover Publications, 2004, ISBN , reprint of the 1907 original edition
• Cayley, Arthur, The collected mathematical papers of Arthur Cayley, I (1841–1853), Cambridge University Press, 1889, 123–126
• Dieudonné, Jean, redaktorAbrégé d'histoire des mathématiques 1700–1900, Paris, FR: Hermann, 1978
• Hawkins, Thomas, "Cauchy and the spectral theory of matrices", Historia Mathematica, 2, 1975: 1–29, doi:10.1016/0315-0860(75)90032-4, ISSN 0315-0860,  0469635
• Knobloch, Eberhard, From Gauss to Weierstrass: determinant theory and its historical evaluations // The interBölmə of history and mathematics, Science Networks Historical Studies, 15, Basel, Boston, Berlin: Birkhäuser, 1994, 51–66,  1308079
• Kronecker, Leopold, Hensel, Kurt (redaktor), Leopold Kronecker's Werke, Teubner, 1897
• Mehra, Jagdish; Rechenberg, Helmut, The Historical Development of Quantum Theory (1st), Berlin, DE; New York, NY: Springer-Verlag, 1987, ISBN 
• Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung, Nine Chapters of the Mathematical Art, Companion and Commentary (2nd), Oxford University Press, 1999, ISBN 
• Weierstrass, Karl, Collected works, 3, 1915