Ellips (q.yun. ἔλλειψις — endirmə, çatışmazlıq) — müstəvi üzərində fokuslar adlanan iki nöqtədən məsafələrinin cəmi sabit olub, fokuslar arasındakı məsafədən böyük qalan nöqtələrin həndəsi yeri.


Ellipsin kanonik tənliyi
Düstur ilə təyini və Ellipsin kanonik tənliyi:
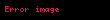
Xüsusi halda 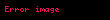
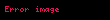
Əlaqəli təyinləri
- Ellips fokusları vasitəsilə keçən və ucu ellipsə uzanan AB parçası, bu ellipsin böyük oxu adlanır. Böyük oxun uzunluğu yuxarıda göstərilən tənlikdə 2a-ya bərabərdir.
- CD parçası - perpendikulyar ellipsin böyük oxunun mərkəzindən keçən və elliə uzanan ox, ellipsin kiçik oxu adlan
- larının kəsişmə nöqtəsi oadl Abbasov eli 1706anır.
- Müstəvi üzərində ixtiyari nöqtənin fokuslardan ibarət
və
məsafəsi bu nöqtənin fokal radiusları adlanır.
- Məsafə tənliyi:
- Bu təyin fokus məsafəsi adlanır.
təyini eliptik ölçü adlanır.
- Ellipsin diametri onun mərkəzindən keçən vətərdir. Ellipsin diametri 2 xüsusiyyətə malikdir: vətərin ortası paralel olaraq birinci diametrdən ikinci diametrə qədər uzanır. Bu halda və vətərin ortası paralel olaraq ikinci diametrdən, birinci diametrə qədər uzanır.
- İxtiyari nöqtədə ellipsin radiusu (mərkəzdən bu nöqtəyə qədər olan məsafə) aşağıdakı düstur ilə hesablanır:
- burada
— bu nöqtənin radius-vektoru ilə absis oxu arasında qalan bucaqdır.
- burada
fokus parametri fokusdan keçən vətər ilə ellipsə perpendikulyar böyük oxun uzunluğunun yarısına bərabərdir.
- Kiçiyin uzunluqlar ilə və böyük yarımoxlar arasındakı əlaqə ellipsin sıxma əmsalı və ya eliptiklik adlanır:
Xüsusiyyətlər
- Optika
- Fokuslardan birində olan mənbədən əks etdirilən işıq şüaları ikinci fokusda kəsişəcək.
- Fokuslardan kənar olan ixtiyari mənbədən ellipsə əks etdirilən şüalar heç bir fokusda kəsişməyəcək.
- Əgər ellipsin fokusları
və
-sə, — onda ellipsə aid olan ixtiyari X nöqtəsi ilə toxunan arasındakı bucağı,
düzü ilə bu toxunanın
düzü arasındakı bucağa bərabərdir.
- Ellipsdən keçən iki paralel düz xətt parçaları həmişə ellipsin mərkəzindən keçir. Bu da ellipsi pərgarın köməyi ilə qurmağa imkan verir. Beləki, xətlər ilə ellipsin mərkəzi, oxları, zirvələri və fokusları asan qurulur.
- , ellipsin evolyutasıdır.
- Oxları ilə ellipsin kəsişmə nöqtələri onun zirvələridir.
- Ellips eliptik əlaqəyə bərabərdir
Eliptik ellipsin uzunluğunu xarakterizə edir. Nə qədər eliptik sıfıra daha yaxın olarsa ellipsin təsvir olunması artır və əks prosesdə isə (yəni sıfırdan böyük) ellips təsviri xatırladır. Eliptik vahidə yaxın olduqda isə, bir o qədər uzadacaqlar.
- Ellipsi təsvir etmək olar:
- çevrəyə affin dəyişikliyini tətbiq edərək;
- çevrənin səthə ortoqonal proyeksiyası ilə;
- Səthin və dairəvi silindrin kəsişməsi ilə;
Ellipsin elementləri arasındakı münasibətlər

— böyük yarım ox;
— kiçik yarım ox;
— fokus məsafəsi (fokuslar arasındakı məsafə);
— fokus parametri;
— perifoks məsafəsi (ellipsdə fokusdan nöqtəyə qədər minimal məsafə);
— apofoks məsafəsi (ellipsdə fokusdan nöqtəyə qədər maksimal məsafə);

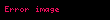

 |  | 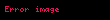 |  |  |  | |
|---|---|---|---|---|---|---|
 – böyük yarım ox – böyük yarım ox |  |  | 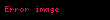 | 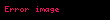 |  |  |
 – kiçik yarım ox – kiçik yarım ox | 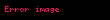 |  | 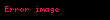 |  | 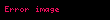 |  |
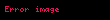 – fokal məsafə – fokal məsafə | 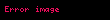 |  | 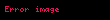 |  | 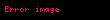 |  |
 – fokal parametr – fokal parametr | 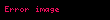 | 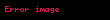 | 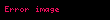 |  | 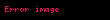 |  |
 – perifoks məsafə – perifoks məsafə | 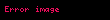 | 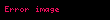 | 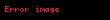 |  |  | 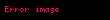 |
 – apofoks məsafə – apofoks məsafə |  |  |  |  |  |  |
Mənbə
- Ali riyaziyyat (lectures) (pdf). Melikov Behruz. səh. səh. 22-27. 2016-04-04 tarixində (PDF). İstifadə tarixi: 2013-12-25. (az.)
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Ellips q yun ἔlleipsis endirme catismazliq mustevi uzerinde fokuslar adlanan iki noqteden mesafelerinin cemi sabit olub fokuslar arasindaki mesafeden boyuk qalan noqtelerin hendesi yeri Ellips fokuslari ve esas oxlariEllipsin konussekilli formasi Fokuslar ve direktrisalar hendesi olaraq Dandelena kurelerinin komeyi ile alinib Ellipsin kanonik tenliyiDustur ile teyini ve Ellipsin kanonik tenliyi x2a2 y2b2 1 displaystyle frac x 2 a 2 frac y 2 b 2 1 Xususi halda a b displaystyle a b olarsa x2 y2 1 displaystyle x 2 y 2 1 cevresi alinar Elaqeli teyinleriEllips fokuslari vasitesile kecen ve ucu ellipse uzanan AB parcasi bu ellipsin boyuk oxu adlanir Boyuk oxun uzunlugu yuxarida gosterilen tenlikde 2a ya beraberdir CD parcasi perpendikulyar ellipsin boyuk oxunun merkezinden kecen ve ellie uzanan ox ellipsin kicik oxu adlan larinin kesisme noqtesi oadl Abbasov eli 1706anir Mustevi uzerinde ixtiyari noqtenin fokuslardan ibaret r1 displaystyle r 1 ve r2 displaystyle r 2 mesafesi bu noqtenin fokal radiuslari adlanir Mesafe tenliyi c F1F2 2 displaystyle c frac F 1 F 2 2 Bu teyin fokus mesafesi adlanir dd e ca 1 b2a2 displaystyle e frac c a sqrt 1 frac b 2 a 2 teyini eliptik olcu adlanir Ellipsin diametri onun merkezinden kecen veterdir Ellipsin diametri 2 xususiyyete malikdir veterin ortasi paralel olaraq birinci diametrden ikinci diametre qeder uzanir Bu halda ve veterin ortasi paralel olaraq ikinci diametrden birinci diametre qeder uzanir Ixtiyari noqtede ellipsin radiusu merkezden bu noqteye qeder olan mesafe asagidaki dustur ile hesablanir r abb2cos2 f a2sin2 f b1 e2cos2 f displaystyle r frac ab sqrt b 2 cos 2 varphi a 2 sin 2 varphi frac b sqrt 1 e 2 cos 2 varphi burada f displaystyle varphi bu noqtenin radius vektoru ile absis oxu arasinda qalan bucaqdir dd p b2a displaystyle p frac b 2 a fokus parametri fokusdan kecen veter ile ellipse perpendikulyar boyuk oxun uzunlugunun yarisina beraberdir Kiciyin uzunluqlar ile ve boyuk yarimoxlar arasindaki elaqe ellipsin sixma emsali ve ya eliptiklik adlanir XususiyyetlerOptika Fokuslardan birinde olan menbeden eks etdirilen isiq sualari ikinci fokusda kesisecek Fokuslardan kenar olan ixtiyari menbeden ellipse eks etdirilen sualar hec bir fokusda kesismeyecek Eger ellipsin fokuslari F1 displaystyle F 1 ve F2 displaystyle F 2 se onda ellipse aid olan ixtiyari X noqtesi ile toxunan arasindaki bucagi F1X displaystyle F 1 X duzu ile bu toxunanin F2X displaystyle F 2 X duzu arasindaki bucaga beraberdir Ellipsden kecen iki paralel duz xett parcalari hemise ellipsin merkezinden kecir Bu da ellipsi pergarin komeyi ile qurmaga imkan verir Beleki xetler ile ellipsin merkezi oxlari zirveleri ve fokuslari asan qurulur ellipsin evolyutasidir Oxlari ile ellipsin kesisme noqteleri onun zirveleridir Ellips eliptik elaqeye beraberdir e ca 1 b2a2 0 e lt 1 displaystyle e frac c a sqrt 1 frac b 2 a 2 0 leqslant e lt 1 Eliptik ellipsin uzunlugunu xarakterize edir Ne qeder eliptik sifira daha yaxin olarsa ellipsin tesvir olunmasi artir ve eks prosesde ise yeni sifirdan boyuk ellips tesviri xatirladir Eliptik vahide yaxin olduqda ise bir o qeder uzadacaqlar Ellipsi tesvir etmek olar cevreye affin deyisikliyini tetbiq ederek cevrenin sethe ortoqonal proyeksiyasi ile Sethin ve dairevi silindrin kesismesi ile Ellipsin elementleri arasindaki munasibetlerEllipsin hisseleri a displaystyle boldsymbol a boyuk yarim ox b displaystyle boldsymbol b kicik yarim ox c displaystyle boldsymbol c fokus mesafesi fokuslar arasindaki mesafe p displaystyle boldsymbol p fokus parametri rp displaystyle boldsymbol r p perifoks mesafesi ellipsde fokusdan noqteye qeder minimal mesafe ra displaystyle boldsymbol r a apofoks mesafesi ellipsde fokusdan noqteye qeder maksimal mesafe a2 b2 c2 displaystyle a 2 b 2 c 2 e ca 1 b2a2 0 e lt 1 displaystyle e frac c a sqrt 1 frac b 2 a 2 0 leqslant e lt 1 p b2a displaystyle p frac b 2 a a displaystyle boldsymbol a b displaystyle boldsymbol b c displaystyle boldsymbol c p displaystyle boldsymbol p rp displaystyle boldsymbol r p ra displaystyle boldsymbol r a a displaystyle boldsymbol a boyuk yarim ox a displaystyle boldsymbol a a b1 e2 displaystyle a frac b sqrt 1 e 2 a ce displaystyle a frac c e a p1 e2 displaystyle a frac p 1 e 2 a rp1 e displaystyle a frac r p 1 e a ra1 e displaystyle a frac r a 1 e b displaystyle boldsymbol b kicik yarim ox b a1 e2 displaystyle b a sqrt 1 e 2 b displaystyle boldsymbol b b c 1 e2e displaystyle b frac c sqrt 1 e 2 e b p1 e2 displaystyle b frac p sqrt 1 e 2 b rp1 e1 e displaystyle b r p sqrt frac 1 e 1 e b ra1 e1 e displaystyle b r a sqrt frac 1 e 1 e c displaystyle boldsymbol c fokal mesafe c ae displaystyle c ae c be1 e2 displaystyle c frac be sqrt 1 e 2 c displaystyle boldsymbol c c pe1 e2 displaystyle c frac pe 1 e 2 c rpe1 e displaystyle c frac r p e 1 e c rae1 e displaystyle c frac r a e 1 e p displaystyle boldsymbol p fokal parametr p a 1 e2 displaystyle p a 1 e 2 p b 1 e2 displaystyle p b sqrt 1 e 2 p c 1 e2e displaystyle p c frac 1 e 2 e p displaystyle boldsymbol p p rp 1 e displaystyle p r p 1 e p ra 1 e displaystyle p r a 1 e rp displaystyle boldsymbol r p perifoks mesafe rp a 1 e displaystyle r p a 1 e rp b 1 e1 e displaystyle r p b sqrt frac 1 e 1 e rp c 1 ee displaystyle r p c frac 1 e e rp p1 e displaystyle r p frac p 1 e rp displaystyle boldsymbol r p rp ra1 e1 e displaystyle r p r a frac 1 e 1 e ra displaystyle boldsymbol r a apofoks mesafe ra a 1 e displaystyle r a a 1 e ra b 1 e1 e displaystyle r a b sqrt frac 1 e 1 e ra c 1 ee displaystyle r a c frac 1 e e ra p1 e displaystyle r a frac p 1 e ra rp 1 e1 e displaystyle r a r p frac 1 e 1 e ra displaystyle boldsymbol r a MenbeAli riyaziyyat lectures pdf Melikov Behruz seh seh 22 27 2016 04 04 tarixinde PDF Istifade tarixi 2013 12 25 az
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans