Ədədlər nəzəriyyəsi

Ədədlər nəzəriyyəsi — riyaziyyatın ilk növbədə tam ədədləri öyrənən bölməsidir. Müasir ədədlər nəzəriyyəsində həm də , transsendent ədədlər kimi ədədlər nəzərdən keçirilir, həmçinin tam ədədlər və onların ümumiləşməsi hesabı ilə bağlı olan müxtəlif mənşəli funksiyalar öyrənilir.

Ədədlər nəzəriyyəsi üzrə tədqiqatlarda elementar və cəbri metodlarla yanaşı həndəsi, analitik üsullar, həmçinin ehtimal nəzəriyyəsinin metodları tətbiq edilir. Öz növbəsində ədədlər nəzəriyyəsi riyazi analizin, həndəsənin, klassik və müasir cəbrin, sıralar nəzəriyyəsinin, ehtimal nəzəriyyəsinin və s. inkişafına təsir göstərmişdir.

Öz metodlarına görə ədədlər nəzəriyyəsi dörd hissəyə bölünür: elementar, analitik, cəbri və həndəsi. Ədədlər nəzəriyyəsinin metodları kriptoqrafiyada, hesablama riyaziyyatında, informatikada geniş istifadə olunur.

Təsnifatı

Elementar ədədlər nəzəriyyəsi

Elementar ədədlər nəzəriyyəsində tam ədədlər riyaziyyatın başqa bölmələrinin metodları istifadə edilmədən öyrənilir. Elementar ədədlər nəzəriyyəsinin əsas istiqamətləri arasında aşağıdakıları qeyd etmək olar:

• Tam ədədlərin bölünməsi nəzəriyyəsi;
• Ən böyük ortaq bölənin və ən kiçik ortaq bölünənin hesablanması üçün Evklid alqoritmi;
• Ədədin sadə vuruqlara ayrılması və hesabın əsas teoremi;
• Modula görə müqayisə nəzəriyyəsi və müqayisə həlli;
• Dövrü kəsrlər, yaxınlaşma nəzəriyyəsi;
• Diofant tənlikləri, yəni qeyri-müəyyən tənliklərin tam (tam ədədlərdə) həlli;
• Tam ədədlərin bəzi siniflərinin öyrənilməsi — mükəmməl ədədlər, Fibonaççi ədədləri, fiqurlu ədədlər və s.
• Kiçik Ferma teoremi və onun ümumiləşməsi: Eyler teoremi;
• Pifaqor üçlüklərinin tapılması, dörd kub haqqında məsələ;
• Əyləncəli riyaziyyat, məsələn, sehirli kvadratların qurulması.

Analitik ədədlər nəzəriyyəsi

Analitik ədədlər nəzəriyyəsində ədədlər və ədədi funksiyalar haqqında iddiaların çıxarılması və isbat edilməsi üçün riyazi (həm həqiqi, həm də kompleks) analizin güclü aparatı, bəzən də diferensial tənliklər nəzəriyyəsi istifadə olunur. Bu, ədədlər nəzəriyyəsinin tədqiqat sahəsini əhəmiyyətli dərəcədə genişləndirməyə imkan verdi. Xüsusilə, buraya aşağıdakı yeni bölmələr daxil edilmişdir:

• Sadə ədədlərin natural ədədlər sırasında və digər ardıcıllıqlarda (məsələn, verilmiş çoxhədlinin qiymətləri arasında) paylanması;
• Natural ədədlərin müəyyən növ (sadə ədədlər, qüvvətlər, fiqurlu ədədlər və s.) toplananların cəmi şəklində göstərilişi (bax: Additiv ədədlər nəzəriyyəsi);
• Diofant yaxınlaşmalar.

Cəbri ədədlər nəzəriyyəsi

Cəbri ədədlər nəzəriyyəsində tam ədəd anlayışı genişlənir, cəbri ədədlər olaraq rasional əmsallı çoxhədlilərin köklərinə baxılır. Cəbri və transsendent ədədlərin ümumi nəzəriyyəsi işlənmişdir. Bu zaman tam ədədlərin analoqu olaraq tam cəbri ədədlər, yəni tam əmsallı unitar çoxhədlilərin kökləri çıxış edir. Tam ədədlərdən fərqli olaraq, tam cəbri ədədlər halqasında faktoriallıq xüsusiyyəti, yəni sadə vuruqlara ayrılmanın yeganəliyi yerinə yetirilməyə bilər.

Cəbri ədədlər nəzəriyyəsinin meydana çıxmasında Diofant tənliklərinin öyrənilməsi, o cümlədən Böyük Ferma teoremini isbat etmək cəhdləri mühüm rol oynamışdır.

${\displaystyle x^{n}=z^{n}-y^{n}=\prod _{i=1}^{n}(z-a_{i}y),}$

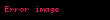
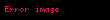
bərabərliyi məxsusdur, burada ${\displaystyle a_{i}}$-lər — vahidin ${\displaystyle n}$-ci dərəcədən kökləridir. Beləliklə, Kummer yeni ${\displaystyle z+a_{i}y}$ şəkilli tam ədədləri təyin etdi. Daha sonra Liuvill göstərdi ki, əgər cəbri ədəd tənliyin ${\displaystyle n}$ dərəcəli köküdürsə, onda ona ${\displaystyle P/Q}$ şəkilində olan kəsrlərlə ${\displaystyle Q^{-n}}$-dən çox yaxınlaşmaq olmaz, burada ${\displaystyle P}$ və ${\displaystyle Q}$ — qarşılıqlı tam ədədlərdir.

Cəbri və transsendent ədədlər təyin edildikdən sonra cəbri ədədlər nəzəriyyəsində iki istiqamət — konkret ədədlərin transsendentliyinin isbatı ilə məşğul olan istiqamət və cəbri ədədləri, onların rasional və cəbri ədədlərlə yaxınlaşma dərəcəsini öyrənən istiqamət ayrılmışdır.

Əsas üsullarından biri cəbri ədədlər sahəsinin öz tamamlayıcısına hər hansı — Arximed (məsələn, həqiqi və ya kompleks ədədlər sahəsinə), yaxud qeyri-Arximed (məsələn, p—adik ədədlər sahəsinə) metrika üzrə daxil edilməsidir.

Həndəsi ədədlər nəzəriyyəsi

Həndəsi ədədlər nəzəriyyəsi əsasən "məkan qəfəslərini" — tam koordinatlı nöqtələr sistemlərini (düzbucaqlı və ya əyrixətli koordinat sistemində) öyrənir. Bu konstruksiyalar həndəsə və kristalloqrafiya üçün böyük əhəmiyyət kəsb edir, onların tədqiqatı kvadratik formaların hesablama nəzəriyyəsi və ədədlər nəzəriyyəsinin digər mühüm bölmələri ilə sıx bağlıdır. Həndəsi ədədlər nəzəriyyəsinin əsasını Herman Minкovski qoymuşdur.

İnkişaf tarixi

Qədim dövrdə ədədlər nəzəriyyəsi

Qədim Misirdə riyazi əməliyyatlar tam ədədlər və alikvot kəsrlər üzərində aparılmışdır. Riyazi papiruslarda həll yolları və köməkçi cədvəllərlə məsələlər saxlanılır. Cədvəllərin daha geniş tətbiqi şümerlərdən sonra altmışlıq say sistemindən istifadə edilmiş Babilistan üçün xarakterikdir. Babil mixi riyazi mətnlərinə vurma və tərs ədədllər, natural ədədlərin kvadratları və kubları cədvəlləri daxildir. Babilistanda çoxlu Pifaqor üçlüyü tanıyırdılar, onları tapmaq üçün, ehtimal ki, naməlum ümumi qaydadan istifadə etmişlər. Hesablama tarixində ən qədim arxeoloji tapıntı — eramızdan əvvəl 1800-cü illərə aid Plimpton 322 gil lövhəsinin fraqmentidir. Onun üzərində Pifaqor üçlüyünün siyahısı, yəni 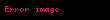${\displaystyle a^{2}+b^{2}=c^{2}}$ şərtini ödəyən ${\displaystyle (a,b,c)}$ natural ədədləri əks olunur. Üçlüklərdə beşrəqəmli ədədlər var və onların sayı variantların mexaniki sayılması ilə əldə edildiyini söyləmək üçün həddindən artıq çoxdur.

Ədədlər nəzəriyyəsinin inkişafına pifaqorçular Evklid və Diofant tərəfindən əhəmiyyətli töhfələr verilmişdir. Pifaqorçular yalnız müsbət tam ədədlərə baxırdılar və ədədi vahidlər toplusu hesab edirdilər. Vahidlər bölünməz və nizamlı həndəsi fiqurlar şəklində düzülmüşdü. Pifaqorçulara "fiqurlu ədədləri" ("üçbucaq", "kvadrat" və s.) müəyyən etmək xasdır. Ədədlərin xassələrini öyrənərək onları cüt və tək, sadə və mürəkkəb ədədlərə böldülər. Ehtimal ki, məhz pifaqorçular yalnız ikiyə bölünmə əlamətindən istifadə edərək sübut edə bilmişlər ki, əgər 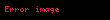${\displaystyle 1+2+...+2^{n}=p}$ sadə ədəddirsə, onda ${\displaystyle 2^{n}p}$ mükəmməl ədəddir. İsbatı Evklidin "Elementlər" kitabında verilmişdir (IX, 36). Yalnız XVIII əsrdə Eyler isbat etdi ki, başqa mükəmməl ədədlər mövcud deyil, mükəmməl ədədlərin sayının sonsuzluğu məsələsi isə hələ də həllini tapmayıb. Pifaqorçular həmçinin ${\displaystyle x^{2}+y^{2}=z^{2}}$ tənliyinin Pifaqor üçlüyü adlandırılan sonsuz tam həllər çoxluğunu tapdılar və onlar üçün ümumi bir düstur əldə etdilər.

Eramızdan əvvəl 399-cu ildə Teetetə məxsus olduğu güman edilən bölünmə nəzəriyyəsi meydana çıxdı. Evklidin VII "Elementlər" kitabı və IX kitabının bir hissəsi buna həsr olunmuşdur. Bu nəzəriyyə iki ədədin ən böyük ortaq bölənini tapmaq üçün Evklid alqoritminə əsaslanır. Alqoritmin nəticəsi istənilən ədədin sadə vuruqlara ayrılmasının mümkünlüyü və bu cür ayrılışın yeganəliyidir. Ədədin sadə vuruqlara ayrılmasının yeganəliyi qanunu tam ədədlər hesabının əsasını təşkil edir.

Evklidin VII, VIII və IX "Elementlər" kitabları sadə ədədlərə və bölünməyə həsr olunmuşdur. Burada, xüsusilə, iki ədədin ən böyük ortaq bölənini tapmaq üçün alqoritm (Evklid alqoritmi) təsvir edilmiş və sadə ədədlər çoxluğunun sonsuz olması isbat edilmişdir.

İskəndəriyyəli Diofant, Qədim Yunanıstanın əvvəlki riyaziyyatçılarından fərqli olaraq, klassik cəbrin məsələlərini həndəsi şəkildə təsvir edərək onları həll etdi. "Hesab" adlı əsərində o, çoxhədli tənliklər sistemlərinin (indiki Diofant tənliklər sistemi) tam həllərinin tapılması üzrə məsələləri sadalayır. Diofantın qeyri-müəyyən tənliklərin rasional ədədlərdə həllinə dair işləri ədədlər nəzəriyyəsi ilə cəbri həndəsənin kəsişməsində dayanır. O, konus kəsiyinin tənliyi olan ikidərəcəli ikidəyişənli ${\displaystyle F_{2}(x,y)=0}$ tənliyini araşdırır. Diofantın, ən azı biri məlum olduqda əyrinin digər rasional nöqtələrini tapmaq üsulu müəyyən edir ki, ikitərtibli əyri ya koordinatları bir parametrli rasional funksiyalar kimi ifadə olunan sonsuz sayda nöqtələrə malikdir, ya da belə nöqtələrə malik deyil. Üçdərəcəli və dörddərəcəli tənliklərin tədqiqi üçün daha mürəkkəb həndəsi üsullardan (rasional nöqtədə toxunanın və ya növbəti kəsişməni tapmaq üçün iki rasional nöqtədən keçən düz xəttin qurulması) istifadə olunur.

Orta əsrlərdə ədədlər nəzəriyyəsi

Çin qalıq teoremi Sun Tzunun "Sun Tzu Suan Jing" (Çin misalları 孙子算经, pinyin sūnzǐ suànjīng) əsərinə misal kimi daxil edilmişdir. Onun həllində mühüm addımlardan biri buraxılmışdı, tam isbatı ilk dəfə eramızın VI əsrində Aryabhata tərəfindən verilmişdir.

Hind riyaziyyatçıları Aryabhata, Brahmaqupta və Bhaskara tam ədədlərdə ${\displaystyle ax+b=cy}$ şəklində olan Diofant tənliklərini həll etdilər. Bundan əlavə, ${\displaystyle ax^{2}+b=y^{2}}$ şəkillı tənliklərin tam həllini tapdılar ki, bu da hind riyaziyyatçılarının ədədlər nəzəriyyəsi sahəsində ən yüksək nailiyyəti idi. Sonradan bu tənlik və onun ${\displaystyle b=1}$ üçün xüsusi halı Ferma, Eyler və Laqranjın diqqətini çəkdi. Həllin tapılması üçün Laqranjın təklif etdiyi üsul hind riyaziyyatçılarınkına yaxın idi.

Ədədlər nəzəriyyəsinin sonrakı inkişafı

Fermanın Diofant tənliklərinin həlli və tam ədədlərin bölünməsi ilə bağlı əsərlərində ədədlər nəzəriyyəsi daha da inkişaf etdirildi. Xüsusilə, Ferma, Fermanın kiçik teoremi adlandırılan belə bir teorem formalaşdırdı ki, istənilən sadə ${\displaystyle p}$ və tam ${\displaystyle a}$ ədədi üçün ${\displaystyle a^{p}-a}$ ədədi ${\displaystyle p}$-yə bölünür. Bundan başqa, o, Fermanın böyük və ya son teoremi adlandırılan ${\displaystyle a^{n}+b^{n}=c^{n}}$ Diofant tənliyinin tam ədədlərdə həll olunmazlığı haqqında teoremi formalaşdırdı. XVIII əsrin əvvəllərində Eyler kiçik teoremin ümumiləşdirməsi və xüsusi hallar üçün böyük teoremin isbatı ilə məşğul olmuşdur. O, həmçinin ədədlər nəzəriyyəsində problemləri həll etmək üçün, funksiyaların generasiyası üsulunu, Eyler eyniliyini, habelə sadə ədədlərin əlavə edilməsi ilə bağlı məsələləri formalaşdıraraq güclü riyazi analiz aparatından istifadə etməyə başladı.

XIX əsrdə bir çox görkəmli alimlər ədədlər nəzəriyyəsi üzərində işləmişlər. Qauss müqayisələr nəzəriyyəsini yaratdı, onun köməyi ilə sadə ədədlər haqqında bir sıra teoremlər isbat edildi, kvadratik çıxıqların və qeyri-çıxıqların xassələri, o cümlədən kvadrat qarşılıqlılıq qanunu öyrənildi. Bu qanunun isbatının tapılması üçün Qauss, sonradan triqonometrik cəmlərə ümumiləşdirilmiş müəyyən tip sonlu sıraları nəzərdən keçirdi. Eylerin işlərini inkişaf etdirərək, Qauss və Dirixle kvadratik formalar nəzəriyyəsini yaratdılar. Bundan əlavə, onlar müstəvidə oblastların tam nöqtələrinin sayına dair bir sıra məsələlər tərtib etdilər ki, onların xüsusi həlləri ${\displaystyle nk+l}$ şəklində silsilələrdə sadə nöqtələrin sayının sonsuzluğu haqqında ümumi teoremi isbat etməyə imkan verdi, burada ${\displaystyle k}$ və ${\displaystyle l}$ qarşılıqlı sadə ədədlərdir. Sadə ədədlərin paylanmasının tədqiqini Çebışev davam etdirdi, o, Evklid teoremindən, sadə ədədlərin sayının sonsuzluğa yaxınlaşması qanununu, daha dəqiq göstərdi, ${\displaystyle (x,2x),x\geq 2}$ intervalında sadə ədədin varlığı haqqında Bertran fərziyyəsini isbat etdi, və eyni zamanda qonşu sadə ədədlər arasındakı fərqin ən kiçik qiymətinin yuxarıdan qiymətləndirilməsi məsələsini qoydu (əkiz sadə ədədlər haqqında məsələnin genişlənməsi).

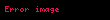
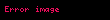
XX əsrin əvvəllərində A. N. Korkin, Y. İ. Zolotarev və A. A. Markov kvadratik formalar nəzəriyyəsi üzərində işləri davam etdirdilər. Korkin və Zolotarev müsbət kvaternar kvadratik formanın dəyişənləri haqqında teoremi isbat etmiş, Markov isə müsbət determinantın binar kvadratik formalarının minimumlarını tədqiq etmişdir. Müstəvi oblastlarındakı tam nöqtələr üçün Dirixle tərəfindən tərtib edilmiş düsturlar G. F. Voronoyun əsərlərində inkişaf etdirildi, o, 1903-cü ildə qalıq həddin tərtibini müəyyən etdi. 1906-cı ildə metod V.Serpinski tərəfindən uğurla dairədə tam ədədlərin sayı haqqında Qauss məsələsinə gətirildi.

1909-cu ildə D.Hilbert Varinqin additiv problemini həll etdi.

Ferma teoremini isbat etməyə çalışan E.Kummer dörd cəbri əməli tətbiq etdiyi ədədlər çoxluğu üçün cəbri ədədlər meydanı ilə işləmiş, və beləliklə, 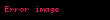${\displaystyle a_{i}}$-lərin doğurduğu cəbri ədədlər meydanının tam ədədlər hesabını qurmuş, ideal vuruqlar anlayışını daxil etmiş və cəbri ədədlər nəzəriyyəsinin yaradılmasına təkan vermişdir. 1844-cü ildə J. Liuvill cəbri və transsendent ədəd anlayışlarını daxil etdi, və beləliklə, Eylerin tam ədədlərin kvadrat kökləri və loqarifmlərinin prinsipial fərqlərə malik olması barədə qeydini riyazi terminlərlə ifadə etdi. Liuvill göstərdi ki, cəbri ədədlər rasional kəsrlərlə zəif yaxınlaşır. XIX əsrin sonlarında Ş. Ermit və F. Lindeman kimi riyaziyyatçılar xüsusi ədədlərin transsendentliyini isbat etmək üzərində işləmişlər – Ş. Ermit 1873-cü ildə ${\displaystyle e}$ ədədinin, F. Lindeman 1882-ci ildə ${\displaystyle \pi }$ ədədinin transsendentliyini isbat etmişdir. Digər istiqamət cəbri ədədlərin rasional və ya cəbri ədədlərlə yaxınlaşma dərəcəsinin öyrənilməsi idi. Bu istiqamətdə işləyən Aksel Tue 1909-cu ildə onun adı ilə adlandırılan teoremi isbat etdi.

Digər istiqamətdə Riemann tərəfindən zeta funksiyasının tərifi verildi, onun analitik olaraq bütün kompleks müstəviyə davam etdiyinin və bir sıra başqa xüsusiyyətlərə malik olmasının isbatı verildi. Riemann həmçinin zeta funksiyasının sıfırları haqqında hipotez irəli sürdü. Zeta funksiyası üzərində işləyərək, Valle Pussen və Jak Adamar 1896-cı ildə sadə ədədlərin paylanması üçün asimptotik qanunu tərtib etdilər. Onların asimptotik düsturları əldə etmək üçün istifadə etdikləri metod, yaxud kompleks inteqrallama üsulu sonralar geniş istifadə olunmağa başladı.

XX əsrin birinci yarısında ədədlər nəzəriyyəsi problemləri üzərində H. Veyl, Q. Hardy, C.Litlvud, A. O. Gelfond, T. Qneyder, K. Zigel, B. N. Delone, D. K. Fadeyev, A.Selberq kimi riyaziyyatçılar çalışmışlar. Herman Veyl tam qiymətli funksiyaların kəsr hissələrinin müntəzəm paylanması üçün münasibətləri formalaşdırmış, Q.Hardy və C.Litlvud additiv məsələlərin həlli üçün dairəvi metod tərtib etmiş, A. O. Qelfond və T. Qneyder Hilbertin 7-ci problemini həll etmiş, K. Zigel funksiyaların qiymətlərinin transsendentliyinə dair bir sıra teoremlər isbat etmiş, B. N. Delone və D. K. Fadeyev 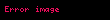${\displaystyle x^{3}-ay^{3}=1}$ Diofant tənliyini tədqiq etmiş, A. Selberq Rieman zeta funksiyasının nəzəriyyəsi üzərində tədqiqatlar aparmıdır.

Ədədlər nəzəriyyəsinin inkişafına böyük töhfə verən İ.M.Vinoqradov parçada kvadrat çıxıqların və qeyri-çıxıqların sayına dair bərabərsizliyi isbat etmiş, Varinq məsələsinin, eləcə də funksiyanın kəsr hissələrinin paylanmasına dair bir sıra məsələlərin həllini sadələşdirməyə, müstəvi və fəza oblastlarında tam nöqtələri təyin etməyə, kritik zolaqda zeta funksiyasının artma tərtibini təyin etməyə imkan verən triqonometrik cəmlər metodunu formalaşdırmışdır. Triqonometrik cəmlərlə bağlı məsələlərdə onların modulunu mümkün qədər dəqiq qiymətləndirmək vacibdir. Vinoqradov belə bir qiymətləndirmə üçün iki üsul təklif etmişdir. Bundan əlavə, o, tələbələri ilə birlikdə Riemann hipotezindən irəli gələn məsələlərin həllinə imkan verən bir sıra üsullar işləyib hazırlamışdır.

Ədədlər nəzəriyyəsinə dair çoxsaylı əsərlər XX əsrin ikinci yarısına aiddir. Y.V.Linnik dispersiya metodunu işləyib hazırladı ki, bu da Hardi-Litlvud problemini və Titçmarçın sadə bölənlər problemi üçün asimptotik düsturlar əldə etməyə imkan verdi. 2003-cü ildə N. M. Səbziyev natural ədədlər ardıcıllığında sadə ədədlərin paylanma funksiyasını vermiş, bu funksiyadan istifadə etməklə istənilən intervalda olan sadə ədədləri və əkiz sadə ədədləri hesablamaq üçün alqoritm təqdim etmişdir. 2004-cü ildə çap olunmuş məqaləsində Səbziyev alqoritminin tətbiqi ilə nümunə üçün hesablanaraq, ${\displaystyle [2\times 10^{9};~2\times 10^{9}+6000]}$ intervalında yerləşən sadə ədədlərin və ${\displaystyle [2\times 10^{9}+6000;~2\times 10^{9}+46000]}$ intervalında yerləşən əkiz sadə ədədlərin cədvəli təqdim edilmişdir.

Eyni zamanda, ədədlər nəzəriyyəsində çoxlu sayda açıq problemlər mövcuddur.

Həmçinin bax

• Теория чисел [3]
• Evklid [4]
• Pifaqor [5]

İstinadlar

1. "Number Theory, page 1 (англ.). Encyclopædia Britannica. Дата обращения: 6 июня 2012. Архивировано 22 июня 2012 года". 2020-09-20 tarixində . İstifadə tarixi: 2022-06-02.
2. Математика, её содержание, методы и значение (в трёх томах). — АН СССР, 1956. — Т. 2. — С. 226–227. — 397 с.
3. Нестеренко Ю. В., 2008, с. 3–6
4. теория чисел // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969–1978
5. История математики. С древнейших времён до начала Нового времени // Под редакцией Юшкевича А. П., в трёх томах. — М.: Наука, 1970. — Т. I.
6. Арифметика // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969–1978.
7. История математики, том I, 1970, с. 37–39.
8. История математики, том I, 1970, с. 50.
9. История математики, том I, 1970, с. 68–69.
10. История математики, том I, 1970, с. 74–76.
11. Number Theory, page 2 (англ.). Encyclopædia Britannica. Дата обращения: 6 июня 2012. Архивировано 22 июня 2012 года.
12. История математики, том I, 1970, с. 146–148.
13. История математики, том I, 1970, с. 146–148. История математики, том I, 1970, с. 194-195.
14. Number Theory, page 3 (англ.). Encyclopædia Britannica. Дата обращения: 6 июня 2012. Архивировано 22 июня 2012 года.
15. Number Theory, page 4 (англ.). Encyclopædia Britannica. Дата обращения: 6 июня 2012. Архивировано 22 июня 2012 года.
16. Number Theory, page 5 (англ.). Encyclopædia Britannica. Дата обращения: 6 июня 2012. Архивировано 22 июня 2012 года
17. Сабзиев Н.М. Распределение простых чисел в натуральном ряду // Известия АН Азерб.ССР. Серия физ.-тех. и матем. наук, 2003, № 3, С. 50-56. [1] 2022-05-27 at the Wayback Machine
18. 'Сабзиев Н.М. Алгоритм составления таблиц простых чисел и простых близнецов // Известия АН Азерб.ССР. Серия физ.-тех. и матем. наук, 2004, Т.XXIV, № 3, С. 35-39. [2] 2022-05-27 at the Wayback Machine
19. "Babayev M.-B., Мusаyев K.M., Таghizadeh Е.D. Azerbaijani Mathematicians. ХХ Century (Математики Азербайджана. ХХ век. Науч. ред. академик Гаджиев А.Д. "ОKA Ofset", Баку, 2007, C.134(175 C.), с. портр., фотогр.)". 2020-02-05 tarixində . İstifadə tarixi: 2022-07-07.

Ədəbiyyat

• М. S. Əkbərov. Ədədlər və fiqurlar aləmində. / Professor Maarif Əkbərov; İxtisas red.: A.P.Bayramov; Rəyçilər: A.Ə.Babayev, M.H.Yaqubov.- B.: Təbib, 1999.- 335 s.[6] [7]
• А. А. Бухштаб. Теория чисел. — М.: Просвещение, 1966 [8]
• И. М. Виноградов. Аналитическая теория чисел // Математическая энциклопедия. — Советская энциклопедия. — М., 1977–1985.[9]
• А. Е. Ингам. Распределение простых чисел. М., 1960. [10]
• А. Я. Хинчин . Три жемчужины теории чисел. М., Наука, 1979, C.64 [11]
  

Xarici keçidlər