Şredinger tənliyi — kvant-mexaniki sistemləri təsvir edən xüsusi törəməli xətti diferensial tənlik; kvant mexanikasının fundamental tənliyi.:1–2 Bu tənlik kvant mexanikasının inkişafında başlıca dönüş nöqtəsi yaratmışdır. Tənlik Ervin Şredingerin adını daşıyır. Şredinger bu tənliyi 1925-ci ildə irəli sürmüş, 1926-cı ildə nəşr etdirmiş, 1933-cü ildə isə bu işinə görə Fizika üzrə Nobel Mükafatı almışdır.

Konseptual olaraq Şredinger tənliyi klassik mexanikadakı Nyutonun ikinci qanununun kvant qarşılığıdır. Bir sıra məlum başlanğıc şərtləri nəzərə aldıqda, Nyutonun ikinci qanunu müəyyən bir fiziki sistemin zamanla hansı yolu keçəcəyinə dair riyazi proqnoz verir. Şredinger tənliyi nın zamana görə evolyusiyasını, təcrid olunmuş fiziki sistemin kvant-mexaniki xarakteristikasını ifadə edir. Tənlik zaman-evolyusiya operatorunun unitarlığı şərtindən çıxarıla bilər və buna görə də kvant Hamiltonianı olan özü-özünə qoşma operatorun üstlü qiymətiylə əldə olunmalıdır.
Şredinger tənliyi kvant-mexaniki sistemləri öyrənmək və proqnozlar vermək üçün yeganə yol deyil. Kvant mexanikasının digər formulyasiyalarına Verner Heyzenberq tərəfindən irəli sürülən matris mexanikası və əsası Riçard Feynman tərəfindən hazırlanmış trayektoriya inteqral formulyasiyası daxildir. Pol Dirak matris mexanikasını və Şredinger tənliyini vahid bir formada birləşdirmişdir. Bu yanaşmaları nəzərə aldıqda, Şredinger tənliyinə əsaslanan mexanikaya bəzən "dalğa mexanikası" da deyilir.
Tərif
Önhazırlıq

Fizika və ya kimyanın giriş kurslarında, adətən, Şredinger tənliyini elə verirlər ki, yalnız diferensial hesabının əsas anlayış və xassələrini, xüsusən də fəza və zamana aid törəmələri bilərək hesablamalar aparmaq mümkün olsun. Bütün bu deyilənləri özündə əks etdirən Şredinger tənliyinin xüsusi halı, tək qeyri-relyativist hissəcik üçün birölçülü mövqe-fəza Şredinger tənliyidir:
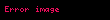
Burada, 


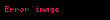
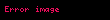
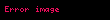

Bu sadə vəziyyətin önünə keçməklə kvant mexanikasının Pol Dirak, David Hilbert, Con fon Neyman və Herman Veyl tərəfindən tərtib edilmiş ciddi riyazi forması kvant-mexaniki sistemin halını 
Maraqlanılan fiziki kəmiyyətlər — mövqe, impuls, enerji, spin — Hilbert fəzasına təsir edən Ermit (daha dəqiq, özü-özünə qoşma) xətti operatorlar olan "müşahidəolunanlar" ilə təmsil olunur. Dalğa funksiyası müşahidəolunabilənin məxsusi vektoru ola bilər, bu halda o, məxsusi hal adlanır və əlaqəli xüsusi qiymət həmin məxsusi halda müşahidəolunanın qiymətinə uyğun gəlir. Daha ümumi şəkildə, kvant halı kvant superpozisiyası kimi tanınan məxsusi halların xətti kombinasiyası olacaqdır. Müşahidəolunabilən ölçüldükdə, nəticə ilə verilmiş ehtimalla onun məxsusi qiymətlərindən biri olacaq: ən sadə halda məxsusi qiymət 


İmpulsun məxsusi halı kvadratik inteqrallanmayan, sonsuz dərəcədə mükəmməl monoxromatik dalğa olacaqdır. Eynilə, mövqenin məxsusi halı Dirak delta paylanması olacaq, o kvadratik inteqrallanmır və texniki cəhətdən ümumiyyətlə funksiya deyil. Nəticə etibarilə, heç biri hissəciyin Hilbert fəzasına aid ola bilməz. Fiziklər bəzən bu fəzanın xaricindəki elementlərdən ibarət Hilbert fəzası üçün həqiqi olmayan "əsaslar" irəli sürürlər. Bunlar hesablama rahatlığı üçün icad edilmişdir və fiziki halları təmsil etmir. Beləliklə, mövqe-fəza dalğa funksiyası 


Zamandan asılı tənlik
Şredinger tənliyinin forması fiziki şəraitdən asılıdır. Ən ümumi forma zamandan asılı Şredinger tənliyidir. O zamana görə dəyişən sistemi təsvir edir:
Burada, 

"Şredinger tənliyi" ifadəsi həm ümumi tənliyi, həm də onun xüsusi qeyri-relyativist versiyanı ifadə edə bilər. Ümumi tənlik həqiqətən də olduqca ümumidir, Dirak tənliyindən tutmuş kvant sahə nəzəriyyəsinə qədər hər şey üçün kvant mexanikasında Hamiltonian üçün müxtəlif ifadələr birləşdirərək istifadə olunur. Xüsusi qeyri-relativist versiya bir çox hallarda, ancaq müəyyən dərəcəyə qədər dəqiq nəticələr verən yaxınlaşmadır.
Şredinger tənliyini tətbiq etmək üçün sistemi təşkil edən hissəciklərin kinetik və potensial enerjilərini nəzərə alaraq sistem üçün Hamiltonian yazılır, sonra o Şredinger tənliyinə daxil edilir. Alınan xüsusi törəməli diferensial tənlik sistem haqqında məlumatı ehtiva edən dalğa funksiyası üçün həll edilir. Praktikada ehtimal sıxlığı funksiyasını təyin etmək üçün hər bir nöqtədə dalğa funksiyasının mütləq qiymətinin kvadratı götürülür. Məsələn, yuxarıdakı kimi mövqe fəzasında 
Zamandan asılı olmayan tənlik
Yuxarıda təsvir edilən zamandan asılı Şredinger tənliyi dalğa funksiyalarının stasionar hallar adlanan durğun dalğalar əmələ gətirə biləcəyini xəbər verir. Bu hallar xüsusilə vacibdir, çünki onların ayrıca tədqiqi sonradan istənilən vəziyyət üçün zamandan asılı Şredinger tənliyinin həll olunması məsələsini asanlaşdırır. Stasionar hallar Şredinger tənliyinin daha sadə forması, zamandan asılı olmayan Şredinger tənliyi ilə də təsvir edilə bilər.

burada 
Xassələr
Xəttilik
Şredinger tənliyi xətti diferensial tənlikdir, yəni iki hal vektoru 
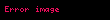
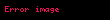
burada a və b ixtiyari kompleks ədədlərdir. Üstəlik, bu cəmi istənilən sayda hal vektoru üçün genişləndirmək olar. Bu xassə kvant hallarının superpozisiyalarının Şredinger tənliyinin həlli olmasına imkan verir. Daha ümumi şəkildə desək, Şredinger tənliyinin ümumi həllini hallar əsasında cəmləmə aparmaqla tapmaq olar. Tez-tez istifadə olunan seçim zamandan asılı olmayan Şredinger tənliyinin həlləri olan məxsusi enerji hallarının əsasıdır. Bu əsasda zamandan asılı hal vektoru 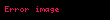
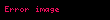
burada 


Unitarlıq


bəzi unitar 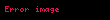
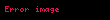

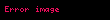
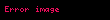
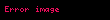
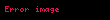


bəzən özü-özünə qoşma 
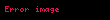
Əsasın dəyişməsi
Şredinger tənliyi tez-tez mövqe funksiyaları kimi dəyişən kəmiyyətlərdən istifadə etməklə verilir, lakin vektor-operator tənliyi kimi Hilbert fəzasında ketlərin istənilən ixtiyari tam bazasında etibarlı təmsilə malikdir. Yuxarıda qeyd edildiyi kimi, fiziki Hilbert fəzasından kənarda yerləşən "əsaslar" da hesablama məqsədləri üçün istifadə olunur. Bu, qeyri-relyativistik, spinsiz hissəcik üçün mövqe-fəza və impuls-fəza Şredinger tənlikləri ilə təsvir edilmişdir. Belə bir hissəcik üçün Hilbert fəzası üçölçülü Evklid fəzasında kompleks kvadratik inteqrallanan funksiyalar fəzasıdır və onun Hamiltonianı impuls operatorunda kvadratik olan kinetik və potensial enerji hədlərinin cəmidir.
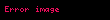
Üçölçülü 

İmpuls-fəza qarşılığı dalğa funksiyasının və potensialın Furye çevrilmələrini əhatə edir:



burada 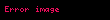
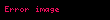


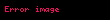


Bu o deməkdir ki,
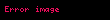
ona görə də mövqe-fəza təsvirində 



Kanonik kommutasiya əlaqəsi həm də mövqe və impuls operatorlarının bir-birinin Furye qoşmaları olduğunu nəzərdə tutur. Nəticə etibarilə, ilkin olaraq mövqedən asılılıq baxımından müəyyən edilmiş funksiyalar Furye çevrilməsindən istifadə edərək impuls funksiyalarına çevrilə bilər. Bərk cisim fizikasında Şredinger tənliyi tez-tez impuls funksiyaları üçün yazılır, çünki Blox teoremi periodik kristal qəfəsin potensial cütlərini təmin etdiyindən, 
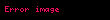

Ehtimal cərəyanı
Şredinger tənliyi yerli ehtimalın saxlanmasına uyğundur. Sağdakı Şredinger tənliyini kompleks qoşma dalğa funksiyasına vurmaq və dalğa funksiyasını Şredinger tənliyinin kompleks qoşmasının soluna vurub çıxmaqla ehtimal üçün kəsilməzlik tənliyini almaq olar:
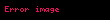
burada

ehtimal sıxlığı (vahid həcmə düşən ehtimal, * kompleks qoşmanı bildirir),
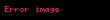
isə ehtimal cərəyanıdır (vahid səthə düşən cərəyandır).
Dəyişənlərə ayrılma
Əgər Hamiltonian zamanın aşkar funksiyası deyilsə, tənlik fəza və zamana aid hissələrin hasili kimi vuruqlara ayrıla bilər. Tənliyi dəyişənlərə ayırma yolu ilə həll etmək, aşağıdakı formanın həllini axtarmaq deməkdir
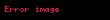
burada 


Bu tip bir həll stasionar adlanır, çünki zamandan asılı olan yeganə şey Born qaydası ilə ehtimal sıxlığı hesablandıqda ləğv edən bir faza amilidir.
Bu, istənilən sayda ölçülər (zamandan asılı olmayan potensialda) istənilən sayda hissəcik üçün ümumiləşdirilir: zamandan asılı tənliyin durğun dalğa həlləri müxtəlif enerjilərin ehtimal paylanması əvəzinə müəyyən enerjiyə malik vəziyyətlərdir. Fizikada bu durğun dalğalar "stasionar vəziyyətlər" və ya "enerji məxsusi halları" adlanır; kimyada onlara "atom orbitalları" və ya "molekul orbitalları" deyilir. Enerjinin məxsusi hallarının superpozisiyaları enerji səviyyələri arasındakı nisbi fazalara uyğun olaraq xassələrini dəyişir. Enerjinin məxsusi halları əsas təşkil edir: hər hansı bir dalğa funksiyası diskret enerji vəziyyətləri üzərində cəmi və ya kəsilməz enerji vəziyyətləri üzərində inteqral və ya daha ümumi olaraq ölçü üzərində inteqral kimi yazıla bilər. Bu, riyaziyyatda spektral teoremdir və sonlu ölçülü vəziyyət fəzasında bu, sadəcə olaraq Ermit matrisinin məxsusi vektorlarının tamlığının ifadəsidir.
Dəyişənlərin ayrılması zamandan asılı olmayan Şredinger tənliyi üçün də səmərəli bir üsul ola bilər. Məsələn, problemin simmetriyasından asılı olaraq, Dekart oxları üzrə
şəklində və ya sferik koordinatlar üzrə aşağıdakı kimi ayrıla bilər:

İstinadlar
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 978-0-13-111892-8.
- "Physicist Erwin Schrödinger's Google doodle marks quantum mechanics work" 2017-08-27 at the Wayback Machine. The Guardian.
- Schrödinger, E. (1926). (PDF). Physical Review. 28 (6): 1049–1070. Bibcode:1926PhRv…28.1049S 2022-04-22 at the Wayback Machine. doi:10.1103/PhysRev.28.1049 2022-09-13 at the Wayback Machine.
- Dirac, Paul Adrien Maurice (1930). The Principles of Quantum Mechanics. Oxford: Clarendon Press.
- von Neumann, John (1932). Mathematische Grundlagen der Quantenmechanik. Berlin: Springer. English translation: Mathematical Foundations of Quantum Mechanics. Translated by Beyer, Robert T. Princeton University Press. 1955.
- Hilbert, David (2009). Sauer, Tilman; Majer, Ulrich (eds.). Lectures on the Foundations of Physics 1915–1927: Relativity, Quantum Theory and Epistemology. Springer. doi:10.1007/b12915 2022-01-19 at the Wayback Machine. ISBN 978-3-540-20606-4. OCLC 463777694 2022-04-12 at the Wayback Machine.
- Weyl, Hermann (1950) [1931]. The Theory of Groups and Quantum Mechanics. Translated by Robertson, H. P. Dover. ISBN 978-0-486-60269-1. Translated from the German Gruppentheorie und Quantenmechanik (2nd ed.). S. Hirzel Verlag. 1931.
- Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2005). Quantum Mechanics. Translated by Hemley, Susan Reid; Ostrowsky, Nicole; Ostrowsky, Dan. John Wiley & Sons. ISBN 0–471–16433-X.
- Shankar, R. (1994). Principles of Quantum Mechanics (2nd ed.). Kluwer Academic/Plenum Publishers. ISBN 978-0-306-44790-7.
- Rieffel, Eleanor G.; Polak, Wolfgang H. (4 March 2011). Quantum Computing: A Gentle Introduction. MIT Press. ISBN 978-0-262-01506-6.
- Yaffe, Laurence G. (2015). "Chapter 6: Symmetries" 2022-05-19 at the Wayback Machine (PDF). Physics 226: Particles and Symmetries.
Xarici keçidlər
- Quantum Cook Book and PHYS 201: Fundamentals of Physics II by , Yale OpenCourseware (ing.)
- The Modern Revolution in Physics – an online textbook. (ing.)
- Quantum Physics I at MIT OpenCourseWare (ing.)
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Sredinger tenliyi kvant mexaniki sistemleri tesvir eden xususi toremeli xetti diferensial tenlik kvant mexanikasinin fundamental tenliyi 1 2 Bu tenlik kvant mexanikasinin inkisafinda baslica donus noqtesi yaratmisdir Tenlik Ervin Sredingerin adini dasiyir Sredinger bu tenliyi 1925 ci ilde ireli surmus 1926 ci ilde nesr etdirmis 1933 cu ilde ise bu isine gore Fizika uzre Nobel Mukafati almisdir Varsava Yeni Texnologiyalar Universitetinin qarsisinda Sredinger tenliyi Oxota kampusu yuxari sagda Konseptual olaraq Sredinger tenliyi klassik mexanikadaki Nyutonun ikinci qanununun kvant qarsiligidir Bir sira melum baslangic sertleri nezere aldiqda Nyutonun ikinci qanunu mueyyen bir fiziki sistemin zamanla hansi yolu kececeyine dair riyazi proqnoz verir Sredinger tenliyi nin zamana gore evolyusiyasini tecrid olunmus fiziki sistemin kvant mexaniki xarakteristikasini ifade edir Tenlik zaman evolyusiya operatorunun unitarligi sertinden cixarila biler ve buna gore de kvant Hamiltoniani olan ozu ozune qosma operatorun ustlu qiymetiyle elde olunmalidir Sredinger tenliyi kvant mexaniki sistemleri oyrenmek ve proqnozlar vermek ucun yegane yol deyil Kvant mexanikasinin diger formulyasiyalarina Verner Heyzenberq terefinden ireli surulen matris mexanikasi ve esasi Ricard Feynman terefinden hazirlanmis trayektoriya inteqral formulyasiyasi daxildir Pol Dirak matris mexanikasini ve Sredinger tenliyini vahid bir formada birlesdirmisdir Bu yanasmalari nezere aldiqda Sredinger tenliyine esaslanan mexanikaya bezen dalga mexanikasi da deyilir TerifOnhazirliq Qeyri relativistik Sredinger tenliyinin V 0 ucun uygun olan dalga funksiyasinin kompleks qrafiki Basqa sozle bu bos fezada serbest hereket eden zerreciye uygundur Fizika ve ya kimyanin giris kurslarinda adeten Sredinger tenliyini ele verirler ki yalniz diferensial hesabinin esas anlayis ve xasselerini xususen de feza ve zamana aid toremeleri bilerek hesablamalar aparmaq mumkun olsun Butun bu deyilenleri ozunde eks etdiren Sredinger tenliyinin xususi hali tek qeyri relyativist hissecik ucun birolculu movqe feza Sredinger tenliyidir iℏ tPS x t ℏ22m 2 x2 V x t PS x t displaystyle i hbar frac partial partial t Psi x t left frac hbar 2 2m frac partial 2 partial x 2 V x t right Psi x t Burada PS x t displaystyle Psi x t dalga funksiyasi olub her bir x displaystyle x noqtesine t displaystyle t aninda mueyyen bir kompleks ededi qarsi qoyur m displaystyle m parametri hisseciyin kutlesi V x t displaystyle V x t ise hisseciyin yerlesdiyi muhiti xarakterize eden potensial i displaystyle i xeyali vahid ℏ displaystyle hbar ise getirilmis Plank sabitidir Bu uc cergenin her biri harmonik ossilyator ucun zamandan asili olan Sredinger tenliyine uygun gelen dalga funksiyasidir Sol Dalga funksiyasinin heqiqi hissesi mavi ve xeyali hissesi qirmizi Sag Verilmis movqede bu dalga funksiyasi ile hisseciyi tapma ehtimalinin paylanmasi Ust iki sira durgun dalgalara uygun gelen stasionar veziyyetlere numunedir Asagi cerge stasionar olmayan veziyyete numunedir Sag sutun stasionar veziyyetlerin niye stasionar adlandirildigini gosterir Bu sade veziyyetin onune kecmekle kvant mexanikasinin Pol Dirak David Hilbert Con fon Neyman ve Herman Veyl terefinden tertib edilmis ciddi riyazi formasi kvant mexaniki sistemin halini H displaystyle mathcal H Hilbert fezasinin ps displaystyle psi rangle vektoruyla ifade edir Bu vektorun Hilbert fezasinin skalyar hasili altinda normallasdirildigi ferz edilir yeni o Dirak notasiyasina tabe olur ps ps 1 displaystyle langle psi psi rangle 1 Hilbert fezasinin tebieti sistemden asilidir meselen movqe ve impulsu tesvir etmek ucun Hilbert fezasi L2 C displaystyle L 2 mathbb C kompleks kvadratik inteqrallanan funksiyalar fezasi tek protonun spini ucun ise sadece olaraq C2 displaystyle mathbb C 2 ikiolculu kompleks vektorlar fezasidir Maraqlanilan fiziki kemiyyetler movqe impuls enerji spin Hilbert fezasina tesir eden Ermit daha deqiq ozu ozune qosma xetti operatorlar olan musahideolunanlar ile temsil olunur Dalga funksiyasi musahideolunabilenin mexsusi vektoru ola biler bu halda o mexsusi hal adlanir ve elaqeli xususi qiymet hemin mexsusi halda musahideolunanin qiymetine uygun gelir Daha umumi sekilde kvant hali kvant superpozisiyasi kimi taninan mexsusi hallarin xetti kombinasiyasi olacaqdir Musahideolunabilen olculdukde netice ile verilmis ehtimalla onun mexsusi qiymetlerinden biri olacaq en sade halda mexsusi qiymet l displaystyle displaystyle lambda cirlasmayandir ve l ps 2 displaystyle langle lambda psi rangle 2 ehtimaliyla verilir Burada l displaystyle lambda rangle rabiteli mexsusi vektordur Daha umumi sekilde mexsusi qiymet cirlasandir ve ps Pl ps displaystyle langle psi P lambda psi rangle ehtimali ile verilir Burada Pl displaystyle P lambda rabiteli mexsusi feza uzre proyektordur Impulsun mexsusi hali kvadratik inteqrallanmayan sonsuz derecede mukemmel monoxromatik dalga olacaqdir Eynile movqenin mexsusi hali Dirak delta paylanmasi olacaq o kvadratik inteqrallanmir ve texniki cehetden umumiyyetle funksiya deyil Netice etibarile hec biri hisseciyin Hilbert fezasina aid ola bilmez Fizikler bezen bu fezanin xaricindeki elementlerden ibaret Hilbert fezasi ucun heqiqi olmayan esaslar ireli sururler Bunlar hesablama rahatligi ucun icad edilmisdir ve fiziki hallari temsil etmir Belelikle movqe feza dalga funksiyasi PS x t displaystyle Psi x t yuxarida istifade edildiyi kimi zamandan asili PS t displaystyle displaystyle Psi t rangle hal vektorunun qeyri fiziki lakin elverisli olan movqenin mexsusi hallari x displaystyle x rangle ile skalyar hasili kimi yazila biler PS x t x PS t displaystyle Psi x t langle x Psi t rangle Zamandan asili tenlik Sredinger tenliyinin formasi fiziki seraitden asilidir En umumi forma zamandan asili Sredinger tenliyidir O zamana gore deyisen sistemi tesvir edir Zamandan asili Sredinger tenliyi umumi hal Burada t displaystyle t zaman PS t displaystyle vert Psi t rangle kvant sisteminin hal vektoru PS displaystyle Psi yunan herfi psidir H displaystyle hat H Hamilton operatorudur Sredinger tenliyi ifadesi hem umumi tenliyi hem de onun xususi qeyri relyativist versiyani ifade ede biler Umumi tenlik heqiqeten de olduqca umumidir Dirak tenliyinden tutmus kvant sahe nezeriyyesine qeder her sey ucun kvant mexanikasinda Hamiltonian ucun muxtelif ifadeler birlesdirerek istifade olunur Xususi qeyri relativist versiya bir cox hallarda ancaq mueyyen dereceye qeder deqiq neticeler veren yaxinlasmadir Sredinger tenliyini tetbiq etmek ucun sistemi teskil eden hisseciklerin kinetik ve potensial enerjilerini nezere alaraq sistem ucun Hamiltonian yazilir sonra o Sredinger tenliyine daxil edilir Alinan xususi toremeli diferensial tenlik sistem haqqinda melumati ehtiva eden dalga funksiyasi ucun hell edilir Praktikada ehtimal sixligi funksiyasini teyin etmek ucun her bir noqtede dalga funksiyasinin mutleq qiymetinin kvadrati goturulur Meselen yuxaridaki kimi movqe fezasinda PS x t displaystyle Psi x t dalga funksiyasi verilmisdirse Pr x t PS x t 2 displaystyle Pr x t Psi x t 2 Zamandan asili olmayan tenlik Yuxarida tesvir edilen zamandan asili Sredinger tenliyi dalga funksiyalarinin stasionar hallar adlanan durgun dalgalar emele getire bileceyini xeber verir Bu hallar xususile vacibdir cunki onlarin ayrica tedqiqi sonradan istenilen veziyyet ucun zamandan asili Sredinger tenliyinin hell olunmasi meselesini asanlasdirir Stasionar hallar Sredinger tenliyinin daha sade formasi zamandan asili olmayan Sredinger tenliyi ile de tesvir edile biler H PS E PS displaystyle operatorname hat H Psi rangle E Psi rangle burada E displaystyle E sistemin enerjisidir Bu yalniz Hamiltonian ozu zamandan askar sekilde asili olmadiqda istifade olunur Bununla bele hetta bu halda umumi dalga funksiyasi asagida xettilik bolmesinde izah edildiyi kimi zamandan asilidir Xetti cebrin diliyle desek bu tenlik mexsusi qiymetli tenlikdir Buna gore de dalga funksiyasi Hamilton operatorunun muvafiq mexsusi qiymet ler i olan mexsusi funksiyasidir XasselerXettilik Sredinger tenliyi xetti diferensial tenlikdir yeni iki hal vektoru ps1 displaystyle psi 1 rangle ve ps2 displaystyle psi 2 rangle hellerdirse onda her hansi bir xetti kombinasiya da tenliyin helli olar ps a ps1 b ps2 displaystyle psi rangle a psi 1 rangle b psi 2 rangle burada a ve b ixtiyari kompleks ededlerdir Ustelik bu cemi istenilen sayda hal vektoru ucun genislendirmek olar Bu xasse kvant hallarinin superpozisiyalarinin Sredinger tenliyinin helli olmasina imkan verir Daha umumi sekilde desek Sredinger tenliyinin umumi hellini hallar esasinda cemleme aparmaqla tapmaq olar Tez tez istifade olunan secim zamandan asili olmayan Sredinger tenliyinin helleri olan mexsusi enerji hallarinin esasidir Bu esasda zamandan asili hal vektoru PS t displaystyle Psi t rangle xetti kombinasiya kimi yazila biler PS t nAne iEnt ℏ psEn displaystyle Psi t rangle sum n A n e iE n t hbar psi E n rangle burada An displaystyle A n ve psEn displaystyle psi E n rangle uygun olaraq kompleks ededler ve vektorlar olub zamandan asili olmayan H psEn En psEn displaystyle H psi E n rangle E n psi E n rangle tenliyinin helleridir Unitarliq H displaystyle hat H Hamilton operatoru sabit olduqda Sredinger tenliyinin helli var PS t e iH t ℏ PS 0 displaystyle Psi t rangle e i hat H t hbar Psi 0 rangle U t e iH t ℏ displaystyle hat U t e i hat H t hbar zaman evolyusiya operatoru adlanan unitar operatordur yeni Hilbert fezasinda vektorlararasi skalyar hasili qoruyur Unitarliq Sredinger tenliyi uzre zaman evolyusiyanin umumi xassesidir Ilkin hal ise PS 0 displaystyle Psi 0 rangle kimidir Bu hal t displaystyle t muddetinden sonra bele olar PS t U t PS 0 displaystyle Psi t rangle hat U t Psi 0 rangle bezi unitar U t displaystyle hat U t operatorlari ucun Eksine ferz edek ki U t displaystyle hat U t t displaystyle t vasitesile parametrlesdirilmis vahid operatorlarin kesilmez ailesidir Umumiliyi pozmadan parametrlesdirme ele secile biler ki U 0 displaystyle hat U 0 her hansi U t N N U t displaystyle hat U t N N hat U t istenilen N gt 0 displaystyle N gt 0 ucun identifikasiya operatoru olsun Bu zaman U t displaystyle hat U t operatorunun t displaystyle t parametrinden asililigi asagidaki kimi olar U t e iG t displaystyle hat U t e i hat G t bezen ozu ozune qosma G displaystyle hat G operatoruna U t displaystyle hat U t ailesinin generatoru deyilir Hamiltonian mehz bele bir generatordur tebii vahidlerde 1 e beraber olan Plank sabitine qeder Esasin deyismesi Sredinger tenliyi tez tez movqe funksiyalari kimi deyisen kemiyyetlerden istifade etmekle verilir lakin vektor operator tenliyi kimi Hilbert fezasinda ketlerin istenilen ixtiyari tam bazasinda etibarli temsile malikdir Yuxarida qeyd edildiyi kimi fiziki Hilbert fezasindan kenarda yerlesen esaslar da hesablama meqsedleri ucun istifade olunur Bu qeyri relyativistik spinsiz hissecik ucun movqe feza ve impuls feza Sredinger tenlikleri ile tesvir edilmisdir Bele bir hissecik ucun Hilbert fezasi ucolculu Evklid fezasinda kompleks kvadratik inteqrallanan funksiyalar fezasidir ve onun Hamiltoniani impuls operatorunda kvadratik olan kinetik ve potensial enerji hedlerinin cemidir iℏddt PS t 12mp 2 V PS t displaystyle i hbar frac d dt Psi t rangle left frac 1 2m hat p 2 hat V right Psi t rangle Ucolculu r displaystyle mathbf r feza ve p displaystyle mathbf p impuls vektorlari ucun movqe feza Sredinger tenliyi asagidaki kimi yazilir iℏ tPS r t ℏ22m 2PS r t V r PS r t displaystyle i hbar frac partial partial t Psi mathbf r t frac hbar 2 2m nabla 2 Psi mathbf r t V mathbf r Psi mathbf r t Impuls feza qarsiligi dalga funksiyasinin ve potensialin Furye cevrilmelerini ehate edir iℏ tPS p t p22mPS p t 2pℏ 3 2 d3p V p p PS p t displaystyle i hbar frac partial partial t tilde Psi mathbf p t frac mathbf p 2 2m tilde Psi mathbf p t 2 pi hbar 3 2 int d 3 mathbf p tilde V mathbf p mathbf p tilde Psi mathbf p t PS r t displaystyle Psi mathbf r t ve PS p t displaystyle tilde Psi mathbf p t funksiyalari PS t displaystyle Psi t rangle funksiyasindan asagidakilarin komeyile alinir PS r t r PS t displaystyle Psi mathbf r t langle mathbf r Psi t rangle PS p t p PS t displaystyle tilde Psi mathbf p t langle mathbf p Psi t rangle burada r displaystyle mathbf r rangle ve p displaystyle mathbf p rangle Hilbert fezasinin ozune aid deyildir lakin bu fezanin butun elementleri ile deqiq mueyyen edilmis skalyar hasillere malikdirler Movqe feza tenliyi uc olcuden bir olcuye dogru mehdudlasdirildiqda movqe feza tenliyi yuxarida verilmis Sredinger tenliyinin yalniz birinci formasidir Kvant mexanikasinda movqe ve impuls arasindaki elaqe bir olcude qiymetlendirile biler Kanonik kvantlamada klassik deyisenler x displaystyle x ve p displaystyle p kanonik kommutasiya elaqesini temin eden x displaystyle hat x ve p displaystyle hat p ozu ozune qosma operatorlara yukseldilir x p iℏ displaystyle hat x hat p i hbar Bu o demekdir ki x p PS iℏddxPS x displaystyle langle x hat p Psi rangle i hbar frac d dx Psi x ona gore de movqe feza tesvirinde p displaystyle hat p impuls operatorunun tesiri beledir iℏddx displaystyle i hbar frac d dx Belelikle p 2 displaystyle hat p 2 ikitertibli toreme olur ve uc olcude ikitertibli toreme 2 displaystyle nabla 2 Laplasian olur Kanonik kommutasiya elaqesi hem de movqe ve impuls operatorlarinin bir birinin Furye qosmalari oldugunu nezerde tutur Netice etibarile ilkin olaraq movqeden asililiq baximindan mueyyen edilmis funksiyalar Furye cevrilmesinden istifade ederek impuls funksiyalarina cevrile biler Berk cisim fizikasinda Sredinger tenliyi tez tez impuls funksiyalari ucun yazilir cunki Blox teoremi periodik kristal qefesin potensial cutlerini temin etdiyinden PS p displaystyle tilde Psi p ile PS p K displaystyle tilde Psi p K yalniz diskret qarsiliqli qefes vektorlari K displaystyle K ucun yazilir Bu Briluen zonasindaki diger noqtelerden asili olmayaraq Briluen zonasinin her bir noqtesinde impuls feza Sredinger tenliyini hell etmeyi asanlasdirir Ehtimal cereyani Sredinger tenliyi yerli ehtimalin saxlanmasina uygundur Sagdaki Sredinger tenliyini kompleks qosma dalga funksiyasina vurmaq ve dalga funksiyasini Sredinger tenliyinin kompleks qosmasinin soluna vurub cixmaqla ehtimal ucun kesilmezlik tenliyini almaq olar tr r t j 0 displaystyle frac partial partial t rho left mathbf r t right nabla cdot mathbf j 0 burada r PS 2 PS r t PS r t displaystyle rho Psi 2 Psi mathbf r t Psi mathbf r t ehtimal sixligi vahid hecme dusen ehtimal kompleks qosmani bildirir j 12m PS p PS PSp PS displaystyle mathbf j frac 1 2m left Psi hat mathbf p Psi Psi hat mathbf p Psi right ise ehtimal cereyanidir vahid sethe dusen cereyandir Deyisenlere ayrilma Eger Hamiltonian zamanin askar funksiyasi deyilse tenlik feza ve zamana aid hisselerin hasili kimi vuruqlara ayrila biler Tenliyi deyisenlere ayirma yolu ile hell etmek asagidaki formanin hellini axtarmaq demekdir PS r t ps r t t displaystyle Psi mathbf r t psi mathbf r tau t burada ps r displaystyle psi mathbf r yalniz sistemi teskil eden hissecik ler in butun feza koordinat lar inin t t displaystyle tau t ise yalniz zamanin funksiyasidir Bu ifadeni PS displaystyle Psi funksiyasinin yerine yazsaq PS r t ps r e iEt ℏ displaystyle Psi mathbf r t psi mathbf r e i Et hbar Bu tip bir hell stasionar adlanir cunki zamandan asili olan yegane sey Born qaydasi ile ehtimal sixligi hesablandiqda legv eden bir faza amilidir Bu istenilen sayda olculer zamandan asili olmayan potensialda istenilen sayda hissecik ucun umumilesdirilir zamandan asili tenliyin durgun dalga helleri muxtelif enerjilerin ehtimal paylanmasi evezine mueyyen enerjiye malik veziyyetlerdir Fizikada bu durgun dalgalar stasionar veziyyetler ve ya enerji mexsusi hallari adlanir kimyada onlara atom orbitallari ve ya molekul orbitallari deyilir Enerjinin mexsusi hallarinin superpozisiyalari enerji seviyyeleri arasindaki nisbi fazalara uygun olaraq xasselerini deyisir Enerjinin mexsusi hallari esas teskil edir her hansi bir dalga funksiyasi diskret enerji veziyyetleri uzerinde cemi ve ya kesilmez enerji veziyyetleri uzerinde inteqral ve ya daha umumi olaraq olcu uzerinde inteqral kimi yazila biler Bu riyaziyyatda spektral teoremdir ve sonlu olculu veziyyet fezasinda bu sadece olaraq Ermit matrisinin mexsusi vektorlarinin tamliginin ifadesidir Deyisenlerin ayrilmasi zamandan asili olmayan Sredinger tenliyi ucun de semereli bir usul ola biler Meselen problemin simmetriyasindan asili olaraq Dekart oxlari uzre ps r psx x psy y psz z displaystyle psi mathbf r psi x x psi y y psi z z seklinde ve ya sferik koordinatlar uzre asagidaki kimi ayrila biler ps r psr r ps8 8 psϕ ϕ displaystyle psi mathbf r psi r r psi theta theta psi phi phi IstinadlarGriffiths David J 2004 Introduction to Quantum Mechanics 2nd ed Prentice Hall ISBN 978 0 13 111892 8 Physicist Erwin Schrodinger s Google doodle marks quantum mechanics work 2017 08 27 at the Wayback Machine The Guardian Schrodinger E 1926 PDF Physical Review 28 6 1049 1070 Bibcode 1926PhRv 28 1049S 2022 04 22 at the Wayback Machine doi 10 1103 PhysRev 28 1049 2022 09 13 at the Wayback Machine Dirac Paul Adrien Maurice 1930 The Principles of Quantum Mechanics Oxford Clarendon Press von Neumann John 1932 Mathematische Grundlagen der Quantenmechanik Berlin Springer English translation Mathematical Foundations of Quantum Mechanics Translated by Beyer Robert T Princeton University Press 1955 Hilbert David 2009 Sauer Tilman Majer Ulrich eds Lectures on the Foundations of Physics 1915 1927 Relativity Quantum Theory and Epistemology Springer doi 10 1007 b12915 2022 01 19 at the Wayback Machine ISBN 978 3 540 20606 4 OCLC 463777694 2022 04 12 at the Wayback Machine Weyl Hermann 1950 1931 The Theory of Groups and Quantum Mechanics Translated by Robertson H P Dover ISBN 978 0 486 60269 1 Translated from the German Gruppentheorie und Quantenmechanik 2nd ed S Hirzel Verlag 1931 Cohen Tannoudji Claude Diu Bernard Laloe Franck 2005 Quantum Mechanics Translated by Hemley Susan Reid Ostrowsky Nicole Ostrowsky Dan John Wiley amp Sons ISBN 0 471 16433 X Shankar R 1994 Principles of Quantum Mechanics 2nd ed Kluwer Academic Plenum Publishers ISBN 978 0 306 44790 7 Rieffel Eleanor G Polak Wolfgang H 4 March 2011 Quantum Computing A Gentle Introduction MIT Press ISBN 978 0 262 01506 6 Yaffe Laurence G 2015 Chapter 6 Symmetries 2022 05 19 at the Wayback Machine PDF Physics 226 Particles and Symmetries Xarici kecidlerQuantum Cook Book and PHYS 201 Fundamentals of Physics II by Yale OpenCourseware ing The Modern Revolution in Physics an online textbook ing Quantum Physics I at MIT OpenCourseWare ing
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State