Elastiklik

Elastiklik — xarici qüvvәlәrin tәsiri ilә forma vә ölçüsünü dәyişәn vә qüvvәlәrin tәsiri kәsildikdәn sonra әvvәlki konfiqurasiyasını alan cisimlәrin xassәsi.

Elastikliyə nümunə

Әksәr materialların (mәsələn, metallarda, dağ süxurlarında, keramikada) kiçik deformasiyaları zamanı gәrginliklər vә deformasiyalar arasındakı asılılıq xәttidir vә onu ümumilәşmiş Huk qanunu ilә tәsvir etmәk olar. Elastiklik modulunu bәzi universal funksiyalarla әvәz etmәklə qeyri-xәtti elastiklik qanunlarını ümumilәşmiş Huk qanununa oxşar formada vermәk mümkündür.

Cisimlәrin elastikliyi onları tәşkil edәn atomların qarşılıqlı tәsir qüvvәlәri ilә şәrtlәnir. Mütlәq sıfır temperaturunda xarici gәrginliklәrin olmadığı bәrk cisimdә atomlar tarazlıq vәziyyәtindәdir. Bu halda hәr bir atoma qalan digәr atomlar tәrәfindәn tәsir edәn bütün qüvvәlәrin cәmi sıfıra, atomun potensial enerjisi isә minimuma bәrabәr olur. Çoxatomlu molekullarda vә makroskopik cismlәrdә yalnız atomlar arasındakı mәsafәdәn asılı olan cazibә vә itәlәmә qüvvәlәrindәn (mәrkәzi qüvvәlәr) başqa, verilmiş atomu onun müxtәlif qonşuları ilә birlәşdirәn düz xәtlәr arasındakı valent bucaqlarından asılı mәrkәzi olmayan qüvvәlәr dә tәsir edir. Valent bucaqlarının tarazlıq qiymәtlәrindә mәrkәzi olmayan qüvvәlәr dә tarazlaşır. Makroskopik cismin enerjisi atomlararası mәsafәdәn vә valent bucaqlarından asılı olub bu parametrlәrin tarazlıq qiymәtlәrindә minimum qiymәt alır.

Xarici qüvvәlәrin tәsiri ilә atomlar tarazlıq vәziyyәtindәn çıxaraq yerlәrini dәyişirlәr. Cismin formasının vә hәcminin dәyişmәsinә sәbәb olan hәmin qüvvәlәrin gördüyü iş qәdәr bu cismin potensial enerjisi artır.

Xarici qüvvәlәrin tәsiri kәsildikdәn sonra elastik cisim öz-özünә tarazlıq vәziyyәtinә qayıdaraq әvvәlki konfiqurasiyasını alır. Cisimdә toplanan artıq potensial enerji rәqs edәn atomların kinetik enerjisinә, yәni istiliyә çevrilir.

Mayelәr (hәmçinin dә qazlar) elastiki formaya deyil, yalnız elastiki hәcmә malikdirlәr: hәcmin kiçilmәsi tәtbiq edilәn tәzyiqlә mütәnasibdir.

Qazların atom vә ya molekulları arasındakı orta mәsafә kifayәt qәdәr böyük olur. Qazların (buxarların) elastikliyi onun hәcmini mәhdudlaşdıran qabın divarları ilə toqquşan molekulların istilik hәrәkәti ilә tәyin edilir.

Ümumi baxış

Elastik material xarici qüvvənin təsiri altında deformasiyaya uğrayan zaman deformasiyaya qarşı daxili müqavimət göstərir və xarici qüvvə götürüldükdən sonra ilkin vəziyyətinə qayıdır. Yunq modulu, sürüşmə modulu və həcmi elastiklik modulu kimi müxtəlif elastiklik modulları var ki, bunların hamısı tətbiq olunan yük altında deformasiyaya müqavimət kimi materialın təbii elastiki xüsusiyyətlərinin ölçüləridir. Müxtəlif modullar müxtəlif növ deformasiyalar üçün uyğundur. Məsələn, Yunq modulu cismin dartılması/sıxılması üçün keçərli ikən, sürüşmə modulu onun sürüşməsi üçün keçərlidir. Yunq modulu və sürüşmə modulu yalnız bərk cisimlərə, həcmi elastiklik modulu isə həm bərk cisimlərə, həm mayelərə, həm də qazlara uyğun gəlir.

Materialların elastikliyi gərginlik (vahid səthə düşən orta daxili qaytarıcı qüvvə) və dartılma (nisbi deformasiya) arasındakı əlaqəni göstərən gərginlik-deformasiya əyrisi ilə təsvir olunur. Əyri ümumiyyətlə qeyri-xəttidir, lakin onu (Teylor sırasından istifadə etməklə) kifayət qədər kiçik deformasiyalar üçün xətti yanaşmayla hesablamaq olar (burada çox yüksək dərəcəli hədlər nəzərdən atılır). Əgər material izotropdursa, xəttiləşdirilmiş gərginlik-deformasiya əlaqəsi Huk qanunu adlanır və bu qanunun əksər metallar və ya kristallik materiallar üçün elastiklik həddinə qədər keçərli olduğu fərz edilir, lakin rezinəbənzər materialların böyük deformasiyalarını modelləşdirmək üçün qeyri-xətti elastiqiyyətin istifadəsi vacibdir. Daha yüksək gərginliklər üçün materiallar plastiki davranış nümayiş etdirir, yəni geri dönməz şəkildə deformasiya olunur və gərginlik götürüldükdən sonra öz ilkin formasına qayıtmır. Elastomerlər kimi rezinəbənzər materiallar üçün gərginlik-deformasiya əyrisinin yamacı gərginliklə artır, yəni rezinlərin uzanması getdikcə çətinləşir, əksər metallar üçün isə qradiyent çox yüksək gərginliklərdə azalır, yəni onların uzanması getdikcə asanlaşır. Elastikliyi yalnız bərk cisimlər nümayiş etdirmir; özlü-elastik mayelər kimi qeyri-Nyuton mayeləri də müəyyən şərtlərdə Debora ədədiylə ölçülən elastiklik nümayiş etdirirlər. Kiçik, sürətlə tətbiq olunan və kənarlaşan gərginliyə cavab olaraq, bu mayelər deformasiya olunduqdan sonra ilkin formasına qayıda bilər. Daha böyük gərginliklər və ya daha uzun müddət tətbiq olunan gərginliklər altında bu mayelər özlü maye kimi axmağa başlaya bilər.

Materialın elastikliyi gərginlik-deformasiya əlaqəsi ilə müəyyən olunduğundan, gərginlik və deformasiya terminlərinin qeyri-müəyyənlik olmadan müəyyən edilməsi vacibdir. Adətən, iki növ əlaqə nəzərə alınır. Birinci növ yalnız kiçik gərginliklər üçün elastik materiallara aiddir. İkincisi, kiçik gərginliklərlə məhdudlaşmayan materiallarla əlaqədardır. Aydındır ki, ikinci növ münasibət o mənada daha ümumidir ki, birinci növü xüsusi hal kimi özündə saxlayır.

Kiçik deformasiyalar üçün istifadə edilən gərginlik ölçüsü Koşi gərginliyi, istifadə olunan gərginlik ölçüsü isə sonsuz kiçilənli deformasiya tenzorudur; ortaya çıxan (təxmin olunan) material davranışı xətti-elastik olub, izotrop mühit üçün ümumiləşdirilmiş Huk qanunu adlanır.

Elastik və hipoelastik Koşi materialları böyük fırlanma, böyük təhriflər və daxili və yaxud induksiyalanmış anizotropiya imkanlarını nəzərə almaq üçün Huk qanununu genişləndirən modellərdir.

Daha ümumi hallar üçün bir sıra gərginlik ölçülərindən hər hansı biri istifadə oluna bilər və ümumiyyətlə arzu edilir (lakin tələb olunmur) elastik gərginlik-deformasiya əlaqəsinin seçilmiş gərginlik ölçüsünə iş konjugatı olan sonlu deformasiya ölçüsü baxımından ifadə edilməsi , yəni gərginlik ölçüsünün daxili hasilinin deformasiya ölçüsünün sürəti ilə zaman inteqralı elastik həddən aşağı qalan hər hansı adiabatik proses üçün daxili enerjinin dəyişməsinə bərabər olmalıdır.

Xətti elastiklik

Yuxarıda qeyd edildiyi kimi, kiçik deformasiyalar üçün, yay kimi elastik materialların əksəriyyəti xətti elastiklik nümayiş etdirir və bu gərginlik və deformasiya arasındakı xətti əlaqə ilə təsvir edilə bilər. Bu əlaqə Huk qanunu kimi tanınır. İdeyanın həndəsədən asılı versiyası ilk dəfə 1675-ci ildə Robert Huk tərəfindən Latın anaqramı olan "ceiiinosssttuv" kimi formulə edilmişdir. O, 1678-ci ildə cavabını nəşr etdirdi: "Ut tensio, sic vis" yəni "Uzanma tətbiq olunan qüvvə ilə düz mütənasibdir" mənasını verir, adətən, Huk qanunu olaraq adlandırılan xətti əlaqəni ifadə edir. Bu qanun dartı qüvvəsi ilə müvafiq x uzanması arasındakı əlaqə kimi ifadə edilə bilər:

${\displaystyle F=kx}$

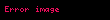
burada k sabit kəmiyyət olub, sərtlik əmsalı adlanır. Həmçinin bu ifadə σ gərginliyi və ε nisbi deformasiyası üçün də yazıla bilər:

${\displaystyle \sigma =E\varepsilon }$

burada E elastiklik modulu (və ya Yunq modulu) adlanır.

Üç ölçüdə gərginlik və nisbi deformasiya arasındakı ümumi mütənasiblik sabiti sərtlik adlanan 4-cü tərtib tenzor olsa da, bir ölçülü çubuq kimi simmetriya nümayiş etdirən sistemlər çox vaxt Huk qanununun tətbiqlərinə gətirilə bilər.

Sonlu elastiklik

Sonlu deformasiyalara məruz qalan cisimlərin elastik davranışı Koşi elastik material modelləri, hipoelastik və hiperelastik material modelləri kimi bir sıra modellərdən istifadə etməklə təsvir edilmişdir. Deformasiya qradiyenti (F) sonlu deformasiya nəzəriyyəsində istifadə olunan əsas deformasiya ölçüsüdür.

Koşi elastik materiallar

Əgər Koşi gərginlik tenzoru σ yalnız deformasiya qradiyenti F-in funksiyası olduqda, material Koşi-elastik hesab olunur:

${\displaystyle \ {\boldsymbol {\sigma }}={\mathcal {G}}({\boldsymbol {F}})}$

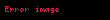
Koşi gərginliyinin sadəcə deformasiya tenzorunun funksiyası olduğunu demək ümumiyyətlə düzgün deyil, çünki belə bir modeldə üfüqi və üfüqi olaraq tətbiq olunan eyni uzanma ilə müqayisədə şaquli uzanmaya məruz qalan anizotrop mühit üçün düzgün nəticələr əldə etmək məqsədilə lazım olan material fırlanması haqqında mühüm məlumat yoxdur və sonra 90 dərəcə fırlanmaya məruz qalır; bu deformasiyaların hər ikisi eyni fəzavi deformasiya tenzorlarına malikdir, lakin Koşi gərginlik tensorunun fərqli qiymətlərini yaratmalıdır.

Koşi-elastik materialda gərginlik yalnız deformasiya vəziyyətindən asılı olsa da, gərginliklərin gördüyü iş deformasiya yolundan asılı ola bilər. Buna görə də, Koşi elastikliyinə konservativ olmayan "qeyri-elastik" modellər (burada deformasiya işi yoldan asılıdır) və həmçinin konservativ "hiperelastik material" modelləri (bunlar üçün gərginlik skalyar "elastik potensial" funksiyasından götürülə bilər) daxildir.

Hipoelastik materiallar

Hipoelastik material ciddi şəkildə aşağıdakı iki kriteriyaya cavab verən konstitutiv tənliklə modelləşdirilmiş material kimi müəyyən edilə bilər:

Koşi gərginliyi ${\displaystyle {\displaystyle {\boldsymbol {\sigma }}}}$ ${\displaystyle t}$ zamanında yalnız cismin öz əvvəlki konfiqurasiyalarını tutma ardıcıllığından asılıdır, lakin bu əvvəlki konfiqurasiyaların keçdiyi zaman sürətindən deyil. Xüsusi hal kimi, bu kriteriyaya Koşi elastik materialı daxildir, onun üçün cari gərginlik əvvəlki konfiqurasiyaların keçmiş vəziyyətindən yox, yalnız cari konfiqurasiyadan asılıdır.

Koşi gərginlik tenzorunun maddi sürəti ${\displaystyle {\dot {\boldsymbol {\sigma }}}=G({\boldsymbol {\sigma }},{\boldsymbol {L}})\,}$olan, ${\displaystyle {\boldsymbol {L}}}$ fəzavi sürət qradiyenti tenzoruna malik tenzor-qiymətli ${\displaystyle G}$ funksiyası mövcuddur.

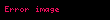
Əgər hipoelastikliyi müəyyən etmək üçün yalnız bu iki orijinal meyardan istifadə olunarsa, o zaman hiperelastiklik xüsusi hal kimi daxil ediləcək və bu, bəzi konstitusiya modelçilərini hipoelastik modelin hiperelastik olmamasını xüsusi olaraq tələb edən üçüncü meyar əlavə etməyə sövq edir (yəni hipoelastiklik stressin enerji potensialından əldə edilə bilməz). Əgər bu üçüncü meyar qəbul edilərsə, bundan belə nəticə çıxır ki, hipoelastik material eyni deformasiya qradiyenti ilə başlayan və bitən, lakin eyni daxili enerjidə başlamayan və bitməyən konservativ olmayan adiabatik yükləmə yollarını qəbul edə bilər.

Qeyd edək ki, ikinci meyar yalnız ${\displaystyle G}$ funksiyasının mövcud olmasını tələb edir. Hipoelastik modellərin spesifik düsturları, adətən, obyektiv dərəcələr adlanır ki, ${\displaystyle G}$ funksiyası yalnız qeyri-aşkar mövcuddur və bir qayda olaraq, faktiki (obyektiv deyil) birbaşa inteqrallama vasitəsilə həyata keçirilən ədədi gərginlik yeniləmələri üçün faktiki gərginlik sürəti tələb olunur.

Hiperelastik materiallar

Hiperelastik materiallar (Qrin elastik materiallar da deyilir) gərginlik enerji sıxlığı funksiyasından (W) əldə edilən konservativ modellərdir. Model o halda hiperelastik sayılır ki, Koşi gərginlik tensorunu deformasiya qradiyenti funksiyası kimi forma əlaqəsi ilə ifadə etmək mümkün olsun.

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {1}{J}}~{\cfrac {\partial W}{\partial {\boldsymbol {F}}}}{\boldsymbol {F}}^{\textsf {T}}\quad {\text{burada}}\quad J:=\det {\boldsymbol {F}}\,}$

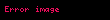
Bu düstur enerji potensialını (W) deformasiya qradiyentinin (${\displaystyle {\boldsymbol {F}}}$) funksiyası kimi qəbul edir. Həmçinin maddi obyektivliyin təmin edilməsini tələb etməklə, enerji potensialı alternativ olaraq Koşi-Yaşıl deformasiya tenzorunun (${\displaystyle {\boldsymbol {C}}:={\boldsymbol {F}}^{\textsf {T}}{\boldsymbol {F}}}$) funksiyası kimi qəbul edilə bilər, bu halda hiperelastik model alternativ olaraq yazıla bilər

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}~{\boldsymbol {F}}{\cfrac {\partial W}{\partial {\boldsymbol {C}}}}{\boldsymbol {F}}^{\textsf {T}}\quad {\text{burada}}\quad J:=\det {\boldsymbol {F}}\,}$

Tətbiqləri

Xətti elastiklik dirəklər, lövhələr, qabıqlar və səndviç kompozitləri kimi strukturların dizaynında və analizində geniş istifadə olunur. Bu nəzəriyyə həm də çatlama mexanikasının xeyli hissəsinin əsasını təşkil edir.

Hiperelastiklik, ilk növbədə, araqat kimi elastomer əsaslı obyektlərin, yumşaq toxuma və hüceyrə membranları kimi bioloji materialların reaksiyasını müəyyən etmək üçün istifadə olunur.

Elastikliyə təsir edən amillər

İzotrop materiallar üçün sınıqların olması Yunq modulu və çatların müstəvilərinə perpendikulyar olan sürüşmə modullarına təsir göstərir ki, bu da qırılma sıxlığı artdıqca azalır (Yunq modulu sürüşmə modulundan daha sürətli), bu da çatların olmasının cisimləri daha kövrək etdiyini göstərir. Mikroskopik olaraq materialların gərginlik-deformasiya əlaqəsi ümumiyyətlə termodinamik kəmiyyət olan Helmholts sərbəst enerjisi ilə idarə olunur. Molekullar, strukturlarından irəli gələn məhdudiyyətlərə tabe olaraq, sərbəst enerjini minimuma endirən konfiqurasiyada yerləşirlər və enerjinin və ya entropiya termininin sərbəst enerjidə üstünlük təşkil etməsindən asılı olaraq, materialları geniş şəkildə enerji-elastik və entropiya-elastik kimi təsnif etmək olar. Beləliklə, molekullar arasındakı tarazlıq məsafəsi kimi sərbəst enerjiyə təsir edən mikroskopik amillər materialların elastikliyinə təsir göstərə bilər: məsələn, qeyri-üzvi materiallarda, 0 K-də molekullar arasındakı tarazlıq məsafəsi artdıqca, həcmi elastiklik modulu azalır. Temperaturun elastikliyə təsirini təcrid etmək çətindir, çünki ona təsir edən çoxsaylı amillər var. Məsələn, materialın həcmi elastiklik modulu onun qəfəsinin formasından, genişlənmə zamanı davranışından, həmçinin molekulların rəqslərindən, bunların hamısı isə temperaturdan asılıdır.

İstinadlar

1. Landau LD, Lipshitz EM. Theory of Elasticity, 3rd Edition, 1970: 1–172.
2. Treloar, L. R. G. The Physics of Rubber Elasticity. Oxford: Clarendon Press. 1975. səh. 2. ISBN .
3. Sadd, Martin H. Elasticity: Theory, Applications, and Numerics. Oxford: Elsevier. 2005. səh. 70. ISBN .
4. de With, Gijsbertus. Structure, Deformation, and Integrity of Materials, Volume I: Fundamentals and Elasticity. Weinheim: Wiley VCH. 2006. səh. 32. ISBN .
5. Material davranışının xarakteristikaları nəzərdən keçirilən materialdan hazırlanmış obyektin həndəsəsindən və formasından müstəqil olmalıdır. Huk qanununun orijinal versiyası obyektin ilkin ölçüsü və formasından asılı olan sərtlik əmsalını ehtiva edir. Buna görə də sərtlik əmsalı ciddi şəkildə material xassəsi deyil.
6. Atanackovic, Teodor M.; Guran, Ardéshir. Hooke's law // Theory of elasticity for scientists and engineers. Boston, Mass.: Birkhäuser. 2000. səh. 85. ISBN .
7. . Centuries of Civil Engineering: A Rare Book Exhibition Celebrating the Heritage of Civil Engineering. Linda Hall Library of Science, Engineering & Technology. 13 November 2010 tarixində orijinalından arxivləşdirilib.
8. Bigoni, D. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press, 2012 . ISBN .
9. Truesdell, Clifford; Noll, Walter. The Non-linear Field Theories of Mechanics (3rd). Berlin Heidelberg New York: Springer-Verlag. 2004. səh. 401. ISBN .
10. Sadd, Martin H. Elasticity: Theory, Applications, and Numerics. Oxford: Elsevier. 2005. səh. 387. ISBN .
11. Sadd, Martin H. Elasticity: Theory, Applications, and Numerics. Oxford: Elsevier. 2005. səh. 344. ISBN .
12. Sadd, Martin H. Elasticity: Theory, Applications, and Numerics. Oxford: Elsevier. 2005. səh. 365. ISBN .