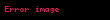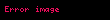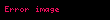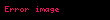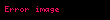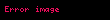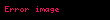Teylor sırası — riyaziyyatda bir funksiyanın, o funksiyanın həddlərinin bir nöqtədəki törəmələrinin qiymətlərindən hesablanan sonsuz toplamı şəklində yazılması formasında açılımdır. Adını ingilis riyaziyyatçı Bruk Teylordan almışdır. Əgər sıra sıfır mərkəzlidirsə (), Teylor sırası daha sadə bir hal alar və bu xüsusi hala şotland riyaziyyatçı istinad olaraq Maklaren sırası deyilir. Bir silsilənin hədlərindən sonlu bir say qədərini istifadə etmək bu silsiləni bir funksiyaya yığmaq üçün ümumi bir üsuldur.


Hər dərəcədən törəməsi olan, həqiqi ya da kompleks bir funskiyasının a həqiqi ya da kompleks bir ədəd olmaq şərtilə intervalındakı Teylor sırası aşağıdakı şəkildə təyin edilir tanımlanmıştır:
Daha nizamlı bir forma olan Siqma təqdimatı ilə isə belə yazılır:
Burada , n faktorialı; ƒ (n)(a) isə f funksiyasının n-ci dərəcədən törəməsinin a nöqtəsindəki qiymətini bildirir. f funksiyasının sıfırıncı dərəcədə n törəməsi f'-in özü ilə təyin edilir və (x − a)0 və 0!, 1-ə bərabər olaraq qəbul edilir.
Xüsusi halda olduqda Teylor sırası
şəklinə düşür. Bu bərabərliyin sağ tərəfindəki sıra adlanır, bərabərlik isə funskiyasının Makloren sırasına ayrılmasıdır.
Aşağıda Teylor sırasının bir neçə nümunəsi verilib:
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Teylor sirasi riyaziyyatda bir funksiyanin o funksiyanin heddlerinin bir noqtedeki toremelerinin qiymetlerinden hesablanan sonsuz toplami seklinde yazilmasi formasinda acilimdir Adini ingilis riyaziyyatci Bruk Teylordan almisdir Eger sira sifir merkezlidirse a 0 displaystyle a 0 Teylor sirasi daha sade bir hal alar ve bu xususi hala sotland riyaziyyatci istinad olaraq Maklaren sirasi deyilir Bir silsilenin hedlerinden sonlu bir say qederini istifade etmek bu silsileni bir funksiyaya yigmaq ucun umumi bir usuldur Teylor coxhedlisinin derecesi artdiqca duz funksiyaya getdikce yaxinlasir Bu sekil sin x displaystyle sin x sinus funksiyasini qara ile ve muxtelif derecelerden olan Teylor acilimlarini 1 3 5 7 9 11 ve 13 gosterir Eksponent quvvet funksiyasi mavi ile gosterilen ve bu funksiyanin a 0 qiymetindeki Teylor sirasinin ilk n 1 heddinin cemi qirmizi ile gosterilen Her dereceden toremesi olan heqiqi ya da kompleks bir f x displaystyle f x funskiyasinin a heqiqi ya da kompleks bir eded olmaq sertile a r a r displaystyle a r a r intervalindaki Teylor sirasi asagidaki sekilde teyin edilir tanimlanmistir f x f a f a 1 x a f a 2 x a 2 f n a n x a n displaystyle f x f a frac f a 1 x a frac f a 2 x a 2 ldots frac f n a n x a n ldots Daha nizamli bir forma olan Siqma teqdimati ile ise bele yazilir n 0 f n a n x a n displaystyle sum n 0 infty frac f n a n x a n Burada n displaystyle n n faktoriali ƒ n a ise f funksiyasinin n ci dereceden toremesinin a noqtesindeki qiymetini bildirir f funksiyasinin sifirinci derecede n toremesi f in ozu ile teyin edilir ve x a 0 ve 0 1 e beraber olaraq qebul edilir Xususi halda a 0 displaystyle a 0 olduqda Teylor sirasi f x f 0 f 0 1 x f 0 2 x 2 f n 0 n x n displaystyle f x f 0 frac f 0 1 x frac f 0 2 x 2 ldots frac f n 0 n x n ldots sekline dusur Bu beraberliyin sag terefindeki sira adlanir beraberlik ise f x displaystyle f x funskiyasinin Makloren sirasina ayrilmasidir Asagida Teylor sirasinin bir nece numunesi verilib ex k 0 x k k 1 x x2 2 x3 3 x lt displaystyle e x sum k 0 infty frac x k k 1 x x 2 2 x 3 3 x lt infty sin x k 0 1 kx 2k 1 2k 1 x x33 x55 x77 x lt displaystyle sin left x right sum k 0 infty 1 k frac x 2k 1 2k 1 approx x frac x 3 3 frac x 5 5 frac x 7 7 x lt infty cos x k 0 1 kx 2k 2k 1 x22 x44 x66 x lt displaystyle cos left x right sum k 0 infty 1 k frac x 2k 2k approx 1 frac x 2 2 frac x 4 4 frac x 6 6 x lt infty 11 x k 0 xn 1 x x2 x3 x4 x lt 1 displaystyle frac 1 1 x sum k 0 infty x n 1 x x 2 x 3 x 4 x lt 1 Riyaziyyat ile elaqedar bu meqale qaralama halindadir Meqaleni redakte ederek Vikipediyani zenginlesdirin Etdiyiniz redakteleri menbe ve istinadlarla esaslandirmagi unutmayin
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans