Dövrün tapılması

İnformatikada dövrün tapılması iterativ funksiyalar ardıcıllığında dövrün tapılması üçün alqoritmik problemdir (alqoritmdir).

Sonlu ${\displaystyle S}$ çoxluğunun özünə uyğun gələn, hər hansı bir ${\displaystyle f}$ funksiyası üçün, və eyni zamanda ${\displaystyle S}$ çoxluğundan olan ${\displaystyle x_{0}}$ başlanğıc nöqtəsi üçün iterativ funksiyalar ardıcıllığı aşağıdakı kimidir:

${\displaystyle x_{0},\ x_{1}=f(x_{0}),\ x_{2}=f(x_{1}),\ \dots ,\ x_{i}=f(x_{i-1}),\ \dots }$

Nəticə etibarilə burada funksiyanın eyni qiyməti aldığı cütlük olmalıdır, yəni elə bir ${\displaystyle i}$ və ${\displaystyle j}$ cütlüyü olmalıdır ki, ${\displaystyle x_{i}=x_{j}}$ şərti ödənmiş olsun. Bu baş verən andan ardıcıllıq dövri olaraq ${\displaystyle x_{i}}$ və ${\displaystyle x_{j-1}}$ aralığında eyni ardıcıllığı təkrarlayacaqdır. Dövrün tapılması məsələsi ${\displaystyle f}$ və ${\displaystyle x_{0}}$-a görə ${\displaystyle i}$ və ${\displaystyle j}$ qiymətlərinin tapılmasıdır.

Bu məsələnin həlli üçün müxtəlif alqoritmlər mövcuddur. Məsələn, "bağa və dovşan alqoritmi" iki göstəricinin müxtəlif sürətlərlə hərəkət etdirilməsi və onlarn hansısa bir nöqtədə rastlaşmasına əsaslanır. alqoritmi isə eksponensial axtarış üsuluna əsaslanıb. Hər iki alqoritm iki göstəricidən istifadə edir. Yaddaşı daha çox istismar etməklə hesablamaları bir qədər azaldan digər müxtəlif alqoritmlər də mövcuddur.

Dövrün tapılması alqoritminin tətbiqi müxtəlifdir, nümunə olaraq psevdo-təsadüfi ədədlər generatoru, , ədədi üsullar üçün alqoritmlər, kompüter proqramlarında və konfiqurasiyalarında sonsuz dövrlərin tapılması və s.

Nümunə

{0,1,2,3,4,5,6,7,8} çoxluğuna uyğun funksiya və qraf

Şəkildə ${\displaystyle ''S''={0,1,2,3,4,5,6,7,8}}$ çoxluğunun özünə uyğun olan ${\displaystyle f}$ funksiyası verilmişdir. Əgər ${\displaystyle x_{0}=2}$ nöqtəsindən başlayaraq ardıcıl olaraq ${\displaystyle f}$ funksiyasını tətbiq etsək aşağıdakı qiymətlər ardıcıllığını alarıq.

2, 0, 6, 3, 1, 6, 3, 1, 6, 3, 1, ....

Burada 6, 3, 1 dövrdür.

Problemin qoyuluşu

Fərz edək ki, ${\displaystyle S}$ sonlu çoxluqdur, ${\displaystyle f}$ isə ${\displaystyle S}$ çoxluğundan özünə olan hər hansı funksiyadır. Burada ${\displaystyle x_{0}}$ ${\displaystyle S}$ çoxluğundan olan bir elementdir. İxtiyari i > 0 üçün x_i = f(x_{i − 1}) qəbul edək.

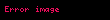
Fərz edək ki, ${\displaystyle x_{\mu }}$ elementi ${\displaystyle x_{i}}$ elementlər ardıcıllığında sonsuz olaraq təkrar olunur və burada ${\displaystyle \mu }$ ən kiçik indeks, ${\displaystyle \lambda }$ (dövrün uzunluğu) isə ən kiçik müsbət ədəddir ki, ${\displaystyle x_{\mu }=x_{\mu +\lambda }}$ bərabərliyini doğru edir. Dövrün tapılması məsələsi ${\displaystyle \lambda }$ və ${\displaystyle \mu }$ ədədlərini tapmaqdan ibarətdir.

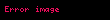
Algorithms

Floyd's Tortoise and Hare

Python proqramlaşdırma dilində kodu:

def floyd(f, x0): # Alqoritmin əsas addımı: x_i = x_2i təkrarlanmasının tapılması. # Dovşan bağadan iki dəfə daha sürətli hərəkət edir və # onlar arasında məsafə hər addımda 1 vahid artır. # Bir vaxt onlar hər ikisi dövrün daxilində olacaqlar, # və onlar arasında məsafə λ ədədinə bölünən olacaq. tortoise = f(x0) # f(x0) qiyməti x0-dan sonrakı element olacaq. hare = f(f(x0)) while tortoise != hare: tortoise = f(tortoise) hare = f(f(hare)) # Bu anda bağanın mövqeyi, ν, (hansı ki, həm də başa ilə dovşan # arasında məsafəyə bərabərdir) λ dövrünə bölünür. # Dovşan dövrün daxilində bir addım olmaqla hərəkət edir,  # başa isə yenidən x0 nöqtəsindən başlayaraq dövrə tərəf hərəkət edir. # intersect at the beginning of the circle. Onlar arasında məsafə # sabit olaraq 2ν, və λ-ya bölünən olduğu üçün, # bağa μ mövqeyinə çatan kimi görüşürlər. # μ görüş yerinin tapılması  mu = 0 tortoise = x0 while tortoise != hare: tortoise = f(tortoise) hare = f(hare) # Dovşan və bağa eyni sürətlə hərəkət edirlər mu += 1 # x_μ-dən başlayaraq ən qısa dövrün tapılması # Dovşan bir addım hərəkət etməkdədir, bağa isə durub. # λ tapılana qədər lam dəyişəni bir vahid artırılır lam = 1 hare = f(tortoise) while tortoise != hare: hare = f(hare) lam += 1 return lam, mu 

Brent-in alqoritmi

Python proqramlaşdırma dilində kodu:

def brent(f, x0): # əsas addım: 2 ədədinin qüvvətinin tapılması power = lam = 1 tortoise = x0 hare = f(x0) # f(x0) - x0-dan sonrakı element/bənd. while tortoise != hare: if power == lam: # 2-nin yeni qüvvəti? tortoise = hare power *= 2 lam = 0 hare = f(hare) lam += 1 # λ uzunluqlu dövrün başlanğıc nöqtəsi mu = 0 tortoise = hare = x0 for i in range(lam): # range(lam) 0, 1, ... , lam-1 qiymətlərindən ibarət siyahı hazırlanır hare = f(hare) # Hazırda dovşan və bağa arasında məsafə λ olur. # Daha sonra dovşan və bağa rastlaşana qədər eyni sürətlə hərəkət edirlər while tortoise != hare: tortoise = f(tortoise) hare = f(hare) mu += 1 return lam, mu 

Tətbiqi

Dövrün tapılması məsələsinin bir çox praktiki tətbiqi vardır.

• Psevdo-təsadüfi ədədlər generatorunun dövrünün uzunluğu onun gücünün əsas meyarlarından biridir. Floydun üsulunu təsvir edərkən bu tətbiqə Knut istinad etmişdir. Brent sınaq nəticələrini təsvir etmişdir. Generatorun dövrü deyilənlərdən daha qısa olduğu ortaya çıxmışdır. Daha mürəkkəb generatorlar üçün, dövrün daxil olduğu qiymətlər ardıcıllığı generatorun çıxışı əvəzinə onun daxili vəziyyətini ifadə edə bilər.
• Bəzi ədədi üsullar alqoritmləri dövrün tapılmasına əsaslanır. Buraya tam ədədlərin faktorizasiyası üçün Pollard-ın rho alqoritmi də aiddir. Həmçinin diskret loqarifmləmə üçün onun də buna nümunədir.
• Kriptoqrafiyada iki müxtəlif x_μ−-1 və x_λ+μ−-1 qiymətlərinin ixtiyari bir f kriptoqrafik funksiyası tərəfindən eyni x_μ qiymətinə uyğun olması onun zəifliyindən xəbər verir. Məsələn, Quisquater və Delescaille dövrün tapılması alqoritmini açarlar cütü və mətnin axtarışı üçün tətbiq edir, harada ki, mətni şifrələnmiş qiymətə uyğun gəlir. , , və dövrün tapılması alqoritmini DES alqoritminə hücum üçün istifadə edirlər. Bu üsul həm də kriptoqrafik həş funksiyalarda kolliziyaların tapılması üçün də istifadə edilə bilər.
• Dövrün tapılması eyni zamanda müxtəlif kompüter proqramlarında sonsuz dövrlərin aşkar edilməsində də praktiki əhəmiyyətə malikdir.
• Hüceyrə avtomatlarının simulyasiyasında periodik konfiqurasiyasların tapılması üçün avtomatın vəziyyətləri ardıcıllığına tətbiq etməklə dövrün tapılması alqoritmindən istifadə səmərəlidir.
• Əlaqəli siyahıların formalarının analizi bu verilənlər strukturundan istifadə edən alqoritmlərin düzgünlüyünün yoxlanılması üçün istifadə olunur. Əgər hər hansı bir bənd səhvən özündən əvvəlki bəndlə əlaqələnibsə o zaman bu siyahıda dövr vardır, hansı ki, onu bu alqoritmlə aşkar etmək olar. dilində, printeri, *print-circle* dəyişəni altında dövrü aşkar edir və yığcam şəkildə çap edir.
• Teske hesablama qrupları nəzəriyyəsində tətbiqi belə təsvir edir: Abel qrupunun strukturunun onun generatorlar çoxluğundan təyin edilməsi. Kalinski və b. tərəfindən kriptoqrafik alqoritmlərə də naməlum qruplarn quruluşunun açılması məsələsi kimi də baxıla bilər.
• Fich, (1981) fəza mexanikasının kompüter simulyasiyasında dövrün tapılması alqoritminin tətbiqini vurğulayır, orada o, -a işarə edir. Burada o, orbital sistemin faza fəzasında dövrün aşkar edilməsinin köməyi ilə sistemin simulyasiya zamanı periyodik olub-olmamasını təyin etmək nəzərdə tutulur.

İstinadlar

1. Joux, Antoine, Algorithmic Cryptanalysis, CRC Press, 2009, səh. 223, ISBN , 2021-08-02 tarixində , İstifadə tarixi: 2017-07-08.
2. , The Art of Computer Programming, vol. II: Seminumerical Algorithms, Addison-Wesley, 1969, səh. 7, exercises 6 and 7
3. , (PDF), , 20 (2), 1980: 176–184, doi:10.1007/BF01933190, 2009-09-24 tarixində orijinalından (PDF) arxivləşdirilib, İstifadə tarixi: 2017-07-08.
4. Pollard, J. M., "A Monte Carlo method for factorization", BIT, 15 (3), 1975: 331–334, doi:10.1007/BF01933667.
5. Pollard, J. M., "Monte Carlo methods for index computation (mod p)", , American Mathematical Society, 32 (143), 1978: 918–924, doi:10.2307/2006496, JSTOR 2006496.
6. Quisquater, J.-J.; Delescaille, J.-P., How easy is collision search? Application to DES // Advances in Cryptology – EUROCRYPT '89, Workshop on the Theory and Application of Cryptographic Techniques, Lecture Notes in Computer Science, 434, Springer-Verlag, 429–434^{[ölü keçid]}.
7. Kaliski, Burton S., Jr.; ; Sherman, Alan T., "Is the Data Encryption Standard a group? (Results of cycling experiments on DES)", , 1 (1), 1988: 3–36, doi:10.1007/BF00206323.
8. Joux, (2009), Section 7.5, Collisions in hash functions, pp. 242–245.
9. Van Gelder, Allen, "Efficient loop detection in Prolog using the tortoise-and-hare technique", Journal of Logic Programming, 4 (1), 1987: 23–31, doi:10.1016/0743-1066(87)90020-3.
10. Nivasch, Gabriel, "Cycle detection using a stack", , 90 (3), 2004: 135–140, doi:10.1016/j.ipl.2004.01.016.
11. Auguston, Mikhail; Hon, Miu Har, Assertions for Dynamic Shape Analysis of List Data Structures // AADEBUG '97, Proceedings of the Third International Workshop on Automatic Debugging, Linköping Electronic Articles in Computer and Information Science, , 1997, 37–42, 2021-08-16 tarixində , İstifadə tarixi: 2017-07-08.
12. Teske, Edlyn, "A space-efficient algorithm for group structure computation", , 67 (224), 1998: 1637–1663, doi:10.1090/S0025-5718-98-00968-5.
13. , Lower bounds for the cycle detection problem // Proc. 13th ACM , 1981, 96–105, doi:10.1145/800076.802462.