Dixotomiya (yun. διχοτομία: δῐχῆ, "iki hissəyə" + τομή, "bölmə") — ikilik və ya bir-birindən daha çox daxildə əlaqəli iki hissəyə bölünmə. Bölünən konsepsiyanın tamamilə iki qarşılıqlı müstəsna konsepsiyaya bölünməsindən ibarət olan bir sinfi məntiqi olaraq alt siniflərə ayırma yolu. Riyaziyyat, fəlsəfə, məntiq və dilçilikdəki ikitərəfli bölgü konsepsiya və ya terminin alt hissələrini formalaşdırma yoludur və elementlərin təsnifatını yaratmağa xidmət edir.

Nümunə
"İnsan" anlayışının əhatə dairəsini iki tamamlayıcı sinifə bölmək olar: kişi və qadın. "Kişilər" və "qadınlar" anlayışları bir-birini tamamlayır.
Başqa bir nümunə aşağıdakılardır: ikiqatlıq, H. Uollesin yazdığı bir əsərdə Avropa Birliyindəki kommunitar və hökumətlərarası idarəetmə metodları arasındakı mənfi fərq olaraq istifadə edilmişdir.
Müsbət və mənfi tərəfləri
Dixotomiya bölgüsü sadəliyi ilə cəlbedicidir. Həqiqətən, ikitirəmlikdə hər zaman bölünən anlayışın əhatəsini tükəndirən yalnız iki siniflə məşğul oluruq. Beləliklə, ikitərəfli bölgü həmişə mütənasibdir; bölünmə üzvləri bir-birini tamamlayır, çünki bölünəcək çoxluğun hər bir obyekti a siniflərindən yalnız birinə düşür ya da а; bölmə bir əsasda həyata keçirilir – bəzi xüsusiyyətlərin olması və ya olmaması. Bölünən konsepsiyanı а hərfi ilə təyin etdikdə və həcmində bir növ, məsələn, b hərfini vurğuladıqda, а həcmini iki hissəyə bölə bilərik — b deyil.
Dixotomiya bölünmənin çatışmazlığı vardır: konsepsiya həcmini iki anlayışa bölərkən, hər dəfə hissənin "deyil" hissəsinin aid olduğu hissəsi son dərəcə qeyri-müəyyən qalır. Alimləri tarixçi və tarixçi olmayanlara ayırsaq, ikinci qrup çox aydın deyil. Bundan əlavə, ikitərəfli bölünmənin başlanğıcında ziddiyyətli bir konsepsiyanın mövcudluğunu müəyyənləşdirmək çox asandırsa, ilk anlayış cütlüyündən uzaqlaşdıqca onu tapmaq daha çətin olur.
Dixotomiya metodu bir hissəyə bölmə metoduna bənzəyir, lakin uçların düşmə meyarı ilə ondan fərqlənir. Əgər funksiya verilibsə 
Zehni olaraq verilmiş seqmenti yarıya böldük və mərkəz 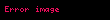
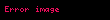
burada 

Tətbiqi
Dixotomiya adətən təsnifat qurulmasında əlavə olaraq istifadə olunur.
Eyni zamanda kifayət qədər geniş istifadə olunan axtarış metodu, yəni ikitirəlik metodu ilə də tanınır. Bəzi meyarlarla müəyyən edilmiş real dəyərli bir funksiyanın dəyərlərini tapmaq üçün istifadə olunur (bu minimum, maksimum və ya müəyyən bir rəqəm üçün müqayisə ola bilər). Şərti bir ölçülü optimallaşdırma üçün ikiqatlıq metodunu nəzərdən keçirin (minimumlaşdırmanın qəti olması üçün).
Dixotomiya metodu
Dixotomiya metodu bir hissəyə bölmə metoduna bənzəyir, lakin uçların düşmə meyarı ilə ondan fərqlənir.

Zehni olaraq verilmiş seqmenti yarıya böldük və mərkəz 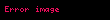
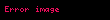
burada 

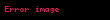
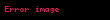
- əgər
varsa,
seqmenti götürülür və
atılır.
- Əks təqdirdə, ortaya nisbətən əks olunan
seqmenti götürülür və
atılır.
Prosedur göstərilən dəqiqliyə çatana qədər təkrarlanır, məsələn, seqment uzunluğu göstərilən xətanın iki qatına çatana qədər.
Hər təkrarda yeni nöqtələr hesablanmalıdır. Növbəti təkrarlamada prosedurun optimallaşdırılmasına əhəmiyyətli dərəcədə kömək edəcək yalnız bir yeni nöqtəni hesablamaq lazım olduğunu əldə etmək mümkündür. Bu, seqmenti qızıl hissədə əks etdirməklə əldə edilir, bu mənada qızıl bölmə metodu 

Ədəbiyyat
- Левитин А. В. Глава 11. Преодоление ограничений: Метод деления пополам // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 476–480. — 576 с. —
- Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. пец. вузов. М.: Высш. шк. 1986.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. М.: Мир. 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы (8-е изд). М.: Лаборатория Базовых Знаний. 2000.
- Волков Е. А. Численные методы. М.: Физматлит. 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. М.: Мир. 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1970. 575–576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. Энергоатомиздат. 1972.
- Максимов Ю. А., Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. М.: МИФИ. 1982.
- Максимов Ю. А. Алгоритмы линейного и дискретного программирования. М.: МИФИ. 1980.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Vikianbarda elaqeli media fayllar Dixotomiya yun dixotomia dῐxῆ iki hisseye tomh bolme ikilik ve ya bir birinden daha cox daxilde elaqeli iki hisseye bolunme Bolunen konsepsiyanin tamamile iki qarsiliqli mustesna konsepsiyaya bolunmesinden ibaret olan bir sinfi mentiqi olaraq alt siniflere ayirma yolu Riyaziyyat felsefe mentiq ve dilcilikdeki ikiterefli bolgu konsepsiya ve ya terminin alt hisselerini formalasdirma yoludur ve elementlerin tesnifatini yaratmaga xidmet edir In ve Yan dixotomiyasiNumune Insan anlayisinin ehate dairesini iki tamamlayici sinife bolmek olar kisi ve qadin Kisiler ve qadinlar anlayislari bir birini tamamlayir Basqa bir numune asagidakilardir ikiqatliq H Uollesin yazdigi bir eserde Avropa Birliyindeki kommunitar ve hokumetlerarasi idareetme metodlari arasindaki menfi ferq olaraq istifade edilmisdir Musbet ve menfi terefleriDixotomiya bolgusu sadeliyi ile celbedicidir Heqiqeten ikitiremlikde her zaman bolunen anlayisin ehatesini tukendiren yalniz iki sinifle mesgul oluruq Belelikle ikiterefli bolgu hemise mutenasibdir bolunme uzvleri bir birini tamamlayir cunki bolunecek coxlugun her bir obyekti a siniflerinden yalniz birine dusur ya da a bolme bir esasda heyata kecirilir bezi xususiyyetlerin olmasi ve ya olmamasi Bolunen konsepsiyani a herfi ile teyin etdikde ve hecminde bir nov meselen b herfini vurguladiqda a hecmini iki hisseye bole bilerik b deyil Dixotomiya bolunmenin catismazligi vardir konsepsiya hecmini iki anlayisa bolerken her defe hissenin deyil hissesinin aid oldugu hissesi son derece qeyri mueyyen qalir Alimleri tarixci ve tarixci olmayanlara ayirsaq ikinci qrup cox aydin deyil Bundan elave ikiterefli bolunmenin baslangicinda ziddiyyetli bir konsepsiyanin movcudlugunu mueyyenlesdirmek cox asandirsa ilk anlayis cutluyunden uzaqlasdiqca onu tapmaq daha cetin olur Dixotomiya metodu bir hisseye bolme metoduna benzeyir lakin uclarin dusme meyari ile ondan ferqlenir Eger funksiya verilibse f x a b R f x C a b displaystyle f x a b to mathrm R f x in mathrm C a b Zehni olaraq verilmis seqmenti yariya bolduk ve merkez x1 displaystyle x 1 ve x2 displaystyle x 2 merkezine dair simmetrik iki noqteni goturek x1 a b2 d x2 a b2 d displaystyle begin array ccc x 1 amp amp frac a b 2 delta x 2 amp amp frac a b 2 delta end array burada delta displaystyle delta left 0 fracb a2 right displaystyle left 0 frac b a 2 right intervalinda bezi reqemlerdir TetbiqiDixotomiya adeten tesnifat qurulmasinda elave olaraq istifade olunur Eyni zamanda kifayet qeder genis istifade olunan axtaris metodu yeni ikitirelik metodu ile de taninir Bezi meyarlarla mueyyen edilmis real deyerli bir funksiyanin deyerlerini tapmaq ucun istifade olunur bu minimum maksimum ve ya mueyyen bir reqem ucun muqayise ola biler Serti bir olculu optimallasdirma ucun ikiqatliq metodunu nezerden kecirin minimumlasdirmanin qeti olmasi ucun Dixotomiya metodu Dixotomiya metodu bir hisseye bolme metoduna benzeyir lakin uclarin dusme meyari ile ondan ferqlenir f x a b R f x C a b displaystyle f x a b to mathrm R f x in mathrm C a b funksiyasi verilibse Zehni olaraq verilmis seqmenti yariya bolduk ve merkez x1 displaystyle x 1 ve x2 displaystyle x 2 merkezine dair simmetrik iki noqteni goturek x1 a b2 d x2 a b2 d displaystyle begin array ccc x 1 amp amp frac a b 2 delta x 2 amp amp frac a b 2 delta end array burada d displaystyle delta intervaldaki bezi reqemler 0 b a2 displaystyle left 0 frac b a 2 right f x displaystyle f x funksiyasinin iki yeni noqtede iki deyerini hesablayaq Muqayise iki yeni noqteden hansinda f x displaystyle f x funksiyasinin deyerinin maksimum oldugunu mueyyen edecekdir Funksiyanin maksimum deyeri olan noqtenin daha yaxin oldugu ilkin seqmentin uclarini ataq xatirla axtaririq yeni eger f x1 gt f x2 displaystyle f x 1 gt f x 2 varsa x1 b displaystyle x 1 b seqmenti goturulur ve a x1 displaystyle a x 1 atilir Eks teqdirde ortaya nisbeten eks olunan a x2 displaystyle a x 2 seqmenti goturulur ve x2 b displaystyle x 2 b atilir Prosedur gosterilen deqiqliye catana qeder tekrarlanir meselen seqment uzunlugu gosterilen xetanin iki qatina catana qeder Her tekrarda yeni noqteler hesablanmalidir Novbeti tekrarlamada prosedurun optimallasdirilmasina ehemiyyetli derecede komek edecek yalniz bir yeni noqteni hesablamaq lazim oldugunu elde etmek mumkundur Bu seqmenti qizil hissede eks etdirmekle elde edilir bu menada qizil bolme metodu d b a 1F 12 displaystyle delta b a left frac 1 Phi frac 1 2 right parametri ile ikiqatliq metodunun yaxsilasdirilmasi kimi qebul edile biler burada F 5 12 1 6180339887 displaystyle Phi frac sqrt 5 1 2 approx 1 6180339887 dots qizil nisbetdir EdebiyyatLevitin A V Glava 11 Preodolenie ogranichenij Metod deleniya popolam Algoritmy Vvedenie v razrabotku i analiz M Vilyams 2006 S 476 480 576 s ISBN 978 5 8459 0987 9 Akulich I L Matematicheskoe programmirovanie v primerah i zadachah Ucheb posobie dlya studentov ekonom pec vuzov M Vyssh shk 1986 Amosov A A Dubinskij Yu A Kopchenova N P Vychislitelnye metody dlya inzhenerov M Mir 1998 Bahvalov N S Zhidkov N P Kobelkov G G Chislennye metody 8 e izd M Laboratoriya Bazovyh Znanij 2000 Volkov E A Chislennye metody M Fizmatlit 2003 Gill F Myurrej U Rajt M Prakticheskaya optimizaciya Per s angl M Mir 1985 Korn G Korn T Spravochnik po matematike dlya nauchnyh rabotnikov i inzhenerov M Nauka 1970 575 576 Korshunov Yu M Korshunov Yu M Matematicheskie osnovy kibernetiki Energoatomizdat 1972 Maksimov Yu A Fillipovskaya E A Algoritmy resheniya zadach nelinejnogo programmirovaniya M MIFI 1982 Maksimov Yu A Algoritmy linejnogo i diskretnogo programmirovaniya M MIFI 1980
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State





