Atlas (topologiya)

Bu adın digər istifadə formaları üçün bax: Atlas (dəqiqləşdirmə).

Riyaziyyatda, xüsusən də topologiyada bir atlasdan istifadə edilərək bir çoxobrazlı təsvir olunur. Atlas, təxminən desək, çeşidli ayrı-ayrı bölgələri təsvir edən fərdi qrafiklərdən ibarətdir. Əgər çoxobrazlı Yerin səthidirsə, onda bir atlasın daha çox ümumi mənası var. Ümumiyyətlə, Atlas anlayışı, çox yönlü və əlaqəli quruluşların, məsələn, vektor dəstələri və digər lif dəstələri kimi formal tərifin əsasını təşkil edir.

Qrafiklər

Bir atlasın tərifi bir qrafik anlayışına bağlıdır. Bir topoloji məkan M üçün cədvəl (koordinat cədvəli, koordinat yaması, koordinat xəritəsi və ya yerli çərçivə də deyilir) bir homeomorfluqdur ${\displaystyle \varphi }$ U açıq bir M-dən Evklid məkanının açıq çoxluqlarlna qədərdir. Qrafik ənənəvi olaraq sifariş edilmiş cüt ${\displaystyle (U,\varphi )}$ olaraq qeyd olunur.

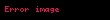
Atlasın ümumi tərifi

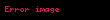
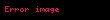
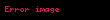
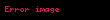
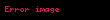
Bir topoloji məkan üçün bir atlas indeksləşdirilmiş ${\displaystyle M}$ ailəsidir ${\displaystyle \{(U_{\alpha },\varphi _{\alpha }):\alpha \in I\}}$ qrafikləru üzərində ${\displaystyle M}$ hansı ki,${\displaystyle M}$ əhatə dairəsini təyin edir(yəni, ${\displaystyle \textstyle \bigcup _{\alpha \in A}U_{\alpha }=M}$). Hər bir cədvəlin kodomaini n ölçülü Evklid məkanıdırsa, onda ${\displaystyle M}$-in n ölçülü bir çoxobrazlı olduğu deyilir.

Bəzi müəlliflər atlastlardan istifadə etsələr də,atlaslar çoxluğu atlaslardır.

Atlas ${\displaystyle \left(U_{i},\varphi _{i}\right)_{i\in I}}$ ${\displaystyle n}$ üzərində ${\displaystyle M}$ ölçülü çoxluq hər bir cədvəlin görüntüsü olduqda, adekvat atlas adlanır,${\displaystyle \mathbb {R} ^{n}}$ or ${\displaystyle \mathbb {R} _{+}^{n}}$, ${\displaystyle \left(U_{i}\right)_{i\in I}}$ ${\displaystyle M}$-in yerli məhdud altçoxluqlar ailələri örtüyüdür,hardaki, ${\displaystyle B_{1}}$ başlanğıc mərkəzində olan radius 1 açıq topdur və ${\displaystyle \mathbb {R} _{+}^{n}}$ qapalı yarım boşluqdur. Hər ikinci sayıla bilən çoxluq adekvat bir atlas qəbul edir. Üstəlik, əgər${\displaystyle {\mathcal {V}}=\left(V_{j}\right)_{j\in J}}$ ikinci sayıla bilən çoxobrazlının açıq örtüyüdürsə, onda ${\displaystyle M}$ orada adekvat bir atlasdır,${\displaystyle \left(U_{i},\varphi _{i}\right)_{i\in I}}$ ${\displaystyle M}$, üzərində belə ${\displaystyle \left(U_{i}\right)_{i\in I}}$ ${\displaystyle {\mathcal {V}}}$ zəifliyidir.

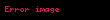
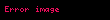
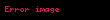
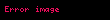
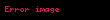
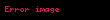
Keçid xəritələri

Bir çoxobrazlıdakı iki qrafik və müvafiq keçid xəritəsi

Bir keçid xəritəsi bir atlasın iki qrafikini müqayisə etmək üçün bir yol təqdim edir. Bu müqayisəni etmək üçün, bir cədvəlin tərkibini digərinin tərsi ilə nəzərdən keçiririk. Bu kompozisiya istisna olmaqla, yaxşı müəyyən edilməmişdir,biz hər iki cədvəlin tərif sahələrinin kəsişməsi ilə məhdudlaşırıq.(Məsələn, Avropanın bir qrafiki və Rusiyanın bir qrafiki varsa, onda bu iki qrafiki üst-üstə düşərsə müqayisə edə bilərik,yəni Rusiyanın Avropa hissəsi.)

Daha dəqiq desək, güman edək ki,${\displaystyle (U_{\alpha },\varphi _{\alpha })}$ və ${\displaystyle (U_{\beta },\varphi _{\beta })}$ belə bir çoxobrazlı M üçün iki qrafikdir,${\displaystyle U_{\alpha }\cap U_{\beta }}$ isə boş çoxluqdur. Keçid xəritəsi ${\displaystyle \tau _{\alpha ,\beta }:\varphi _{\alpha }(U_{\alpha }\cap U_{\beta })\to \varphi _{\beta }(U_{\alpha }\cap U_{\beta })}$ tərəfindən təyin olunan xəritədir:

${\displaystyle \tau _{\alpha ,\beta }=\varphi _{\beta }\circ \varphi _{\alpha }^{-1}.}$

Qeyd edək ki,${\displaystyle \varphi _{\alpha }}$ və ${\displaystyle \varphi _{\beta }}$ hər iki homeomorfluqdur, keçid xəritəsi ${\displaystyle \tau _{\alpha ,\beta }}$ eyni zamanda bir homeomorfluqdur.

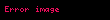
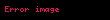
Quruluşları

Biri tez-tez sadəcə topoloji quruluşdan daha çoxbir çoxobrazlıda daha çox quruluş istəyir. Məsələn, törəmə funksiyaların fərqləndirilməsi barədə birmənalı bir anlayış istəsən, keçid funksiyaları bir-birindən fərqlənən bir atlas qurmaq lazımdır. Fərqlənən bir müxtəlifliyi nəzərə alsaq, birmənalı olaraq tangent vektorlar və sonra yönlü törəmələr anlayışını təyin etmək olar.

Hər bir keçid funksiyası hamar bir xəritədirsə, onda atlas hamar atlas, çoxobrazlının özü isə hamar adlanır. Alternativ olaraq, keçid xəritələrində yalnız k davamlı törəmələrin olmasını tələb etmək olar, bu halda atlasın 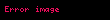${\displaystyle C^{k}}$ olduğu deyilir.

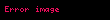
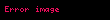
Ümumiyyətlə, hər bir keçid funksiyası bir yalançı qrup çevrilmələrinə aiddirsə,${\displaystyle {\mathcal {G}}}$ Evklid məkanının homeomorfluqlarıdır, onda atlasa ${\displaystyle {\mathcal {G}}}$ — atlas deyilir.

Bir atlasın qrafikləri arasındakı keçid xəritələri yerli trivializasiyanı qorusa, sonra atlas bir lif dəstəsinin quruluşunu təyin edir.

Həmçinin bax

• Homeomorfluq
• Törəmə
• Topologiya

İstinadlar

1. Jost, Jürgen. "Riemannian Geometry and Geometric Analysis". Springer Science & Business Media. 11 November 2013. 4 April 2022 tarixində . İstifadə tarixi: 16 April 2018 – Google Books vasitəsilə.
2. Giaquinta, Mariano; Hildebrandt, Stefan. "Calculus of Variations II". Springer Science & Business Media. 9 March 2013. 4 April 2022 tarixində . İstifadə tarixi: 16 April 2018 – Google Books vasitəsilə.
3. Kosinski, Antoni. Differential manifolds. Mineola, N.Y: Dover Publications. 2007. ISBN . OCLC 853621933.

Ədəbiyyat

• Lee, John M. Introduction to Smooth Manifolds. Springer-Verlag. 2006. ISBN .
• Sepanski, Mark R. Compact Lie Groups. Springer-Verlag. 2007. ISBN .
• Husemoller, D, Fibre bundles, Springer, 1994, Chapter 5 "Local coordinate description of fibre bundles".

Xarici keçidlər

• Atlas Rouland Todd tərəfindən