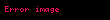Şepard lemması mikroiqtisadiyyatda mühüm bir anlayışdır, və üzrə tədbiq olunur. Lemmaya uyğun olaraq, əgər xərc funksiyasının fərqsizlik əyriləri qabarıqdırsa, onda qiymətə olan müəyyən bir məhsulun xərclərini minimallaşdıran nöqtə yeganədir. İdeya ondan ibarətdir ki, verilmiş bazar qiymətləri ilə istehlakçı müəyyən bir fayda əldə etməyin xərcini minimallaşdırmaq üçün hər bir məhsulun ideal miqdarı alacaq. Lemma şərəfinə adlandırılmışdır, kim ki öz kitabında onun riyazi sübutunu göstərib.
Eyni nəticə istehlak nəzəriyyəsi məzmununda Laynel V. Makkenzi (Lionel W. McKenzie) 1957-ci ildə də alınıb. Ona müvafiq olaraq, xərc funksiyasının məhsul qiymətləri üzrə xüsusi törəmələri münasib məhsullar üçün Hiks tələb funksiyaları ilə bərabərdir. Eyni nəticələr Con Hiks (John Hicks) (1939) və Pol Samuelson (Paul Samuelson) (1947) tərəfindən əldə olunub.
Təyin etmə
İstehlakçı nəzəriyyəsində Şepardın lemması deyir ki, verilmiş "u" fayda dərəcəsi və "p" qiymətlər üçün müəyyən bir i məhsula tələb xərc funksiyasının müəyyən məhsulun qəyməti üzrə törəməsinə bərabərdir.
Harda ki hi(p, u) 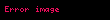

Harda ki xi(w, y) 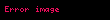

Əlavə materiallar
- Hal Varian, Microeconomic Analysis, p. 74, W. W. Norton & Company (1992) Inc
- Volker Böhm and Hans Haller (1987). "Demand theory," The New Palgrave: A Dictionary of Economics, v. 1
İstinadlar
- Ronald Shepard, Theory of Cost and Production Functions (Princeton University Press, 1953)
- Lionel W. McKenzie, "Demand Theory Without a Utility Index", The Review of Economic Studies, 1957.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Separd lemmasi mikroiqtisadiyyatda muhum bir anlayisdir ve uzre tedbiq olunur Lemmaya uygun olaraq eger xerc funksiyasinin ferqsizlik eyrileri qabariqdirsa onda pi displaystyle p i qiymete olan mueyyen bir mehsulun xerclerini minimallasdiran noqte yeganedir Ideya ondan ibaretdir ki verilmis bazar qiymetleri ile istehlakci mueyyen bir fayda elde etmeyin xercini minimallasdirmaq ucun her bir mehsulun ideal miqdari alacaq Lemma serefine adlandirilmisdir kim ki oz kitabinda onun riyazi subutunu gosterib Eyni netice istehlak nezeriyyesi mezmununda Laynel V Makkenzi Lionel W McKenzie 1957 ci ilde de alinib Ona muvafiq olaraq xerc funksiyasinin mehsul qiymetleri uzre xususi toremeleri munasib mehsullar ucun Hiks teleb funksiyalari ile beraberdir Eyni neticeler Con Hiks John Hicks 1939 ve Pol Samuelson Paul Samuelson 1947 terefinden elde olunub Teyin etmeIstehlakci nezeriyyesinde Separdin lemmasi deyir ki verilmis u fayda derecesi ve p qiymetler ucun mueyyen bir i mehsula teleb xerc funksiyasinin mueyyen mehsulun qeymeti uzre toremesine beraberdir hi p u e p u pi displaystyle h i mathbf p u frac partial e mathbf p u partial p i Harda ki hi p u i displaystyle i mehsulu ucun Hiks telebidir e p u xerc funksiyasidir ve funksiyalarin ikisi p qiymetlerinden ve u displaystyle u faydasindan asilidirlar Habele lemma eyni cur ucun her bir serf olunan faktor uzre ifade olunur c w y xerc funksiyasinin faktorun qiymeti uzre toremesi xi w y c w y wi displaystyle x i mathbf w y frac partial c mathbf w y partial w i Harda ki xi w y i displaystyle i serf olunan faktoru ucun sertli faktor telebinin funksiyasidir c w y qiymet funksiyasidir ve funksiyalarin ikisi w faktorun qiymetleri ve y displaystyle y hasilati uzre teyin olunub Muasir zamanda Separdin lemmasi ile subut olunur Elave materiallarHal Varian Microeconomic Analysis p 74 W W Norton amp Company 1992 Inc ISBN 0 393 95735 7 Volker Bohm and Hans Haller 1987 Demand theory The New Palgrave A Dictionary of Economics v 1IstinadlarRonald Shepard Theory of Cost and Production Functions Princeton University Press 1953 Lionel W McKenzie Demand Theory Without a Utility Index The Review of Economic Studies 1957
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State