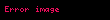Mikroiqtisadiyyatda istehlakçının Hiks tələbinə müvafiqliyi ona təyin edilmiş fayda gətirən və xərclərini minimallaşdıran məhsulların dəstəsinə tələbi bildirir. Əgər bu müvafiqlik müəyyən bir funksiyadır, onda ona Hiks tələb funksiyası, və ya əvəzini verən tələb funksiyası deyilir. Funksiya Con Hiks (John Hicks) şərəfinə adlandırılmışdır. Riyazi şəkildə:
Harda ki h(p,u) Hiks tələb funksiyasıdır, və ya tələb olunan məhsul dəstəsidir, p qiymətləri səviyyəsidir, və faydadır. Burda p qiymətlərin vektorudur, və X tələb olunan miqdarların vektorudur. Deməli bütün pixi cəmi X məhsullarına gedən ümumi xərcdir.
Digər funksiyalar ilə əlaqələr
Hiks tələb funksiyaları riyazi hesablarda işlətmək asandır çünki onlar gəlirin olduğunu tələb etmirlər. Əlavə olaraq, minimallaşdırılmış olmalı funksiya 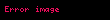

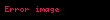
Harda 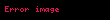
Harda 
Deməli Marşal tələbi faydanı maksimallaşdırmaq problemindən gəlir, Hiks tələbi isə xərci minimallaşdırmaq problemindən. Beləliklə hər iki problem ikitərəflidir, və İkitərəflik Teoremı yuxarıda qeyd olunmuş əlaqələri sübut etməyin üsulunu təklif edir.
Hiks tələb funksiyası çox xərc funksiyasından asılıdır. Əgər istehlakçının fayda funksiyası 

İstinadlar
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Mikroiqtisadiyyatda istehlakcinin Hiks telebine muvafiqliyi ona teyin edilmis fayda getiren ve xerclerini minimallasdiran mehsullarin destesine telebi bildirir Eger bu muvafiqlik mueyyen bir funksiyadir onda ona Hiks teleb funksiyasi ve ya evezini veren teleb funksiyasi deyilir Funksiya Con Hiks John Hicks serefine adlandirilmisdir Riyazi sekilde h p u arg minx ipixi displaystyle h p bar u arg min x sum i p i x i such that u x u displaystyle rm such that u x geq bar u Harda ki h p u Hiks teleb funksiyasidir ve ya teleb olunan mehsul destesidir p qiymetleri seviyyesidir ve u displaystyle bar u faydadir Burda p qiymetlerin vektorudur ve X teleb olunan miqdarlarin vektorudur Demeli butun pixi cemi X mehsullarina geden umumi xercdir Diger funksiyalar ile elaqelerHiks teleb funksiyalari riyazi hesablarda isletmek asandir cunki onlar gelirin oldugunu teleb etmirler Elave olaraq minimallasdirilmis olmali funksiya xi displaystyle x i uzre xettidir ve bu optimizasiya problemini asanlasdirir Amma verilmis p qiymetleri ve w displaystyle w geliri ile telebi tesvir eden x p w displaystyle x p w Marsal teleb funksiyasini birbasa musahide etmek daha asandir Her ikisi bir biri ile adi sekilde elaqededir h p u x p e p u displaystyle h p u x p e p u Harda e p u displaystyle e p u mexaric funksiyasidir verilmis fayda elde etmek ucun minimal geliri gosteren funksiya h p v p w x p w displaystyle h p v p w x p w Harda v p w displaystyle v p w verilmis qiymetler ve mueyyen gelir ile elde edilen faydani gosteren funksiya Onlarin toremelerinin elaqesi daha etrafli Slatski dusturu ile ifade olunur Demeli Marsal telebi faydani maksimallasdirmaq probleminden gelir Hiks telebi ise xerci minimallasdirmaq probleminden Belelikle her iki problem ikitereflidir ve Ikitereflik Teoremi yuxarida qeyd olunmus elaqeleri subut etmeyin usulunu teklif edir Hiks teleb funksiyasi cox xerc funksiyasindan asilidir Eger istehlakcinin fayda funksiyasi u x displaystyle u x ve onda h p u pe p u displaystyle h p u nabla p e p u Istinadlar Iqtisadiyyat haqqinda olan bu meqale qaralama halindadir Meqaleni redakte ederek Vikipediyani zenginlesdirin
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans