Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Bu məqaləni lazımdır. |
Bu teoremi "Hesab" kitabının ikinci hissəsində, 8-ci məsələnin qarşısında yazmışdı: "Verilən kvadartı iki kvadrata ayırın". Başqa sözlə desək, verilmiş a ədədi üçün x2 + y2 = a2 tənliyini rasional həllərini tapmaq tələb olunur. Bu da ki bizlərə çox yaxşı tanış olan Pifaqor teoremidir və onun sonsuz sayda həlli var. Ferma qeyd etmişdir: "Kubu iki kuba, kvadratın kvadratını iki kvadratın kvadratına, ümumiyyətlə dərəcəsi ikidən böyük sonsuzluğa qədər heç bir qüvvəti bütün həmin dərəcəli iki qüvvətə ayırmaq olmaz. Mən bunun həqiqətən çox gözəl isbatını tapmışam, ama onun üçün yer olduqca azdır". Tutaq ki, bizə belə bir məsələ verilib:
Verilmiş tam müsbət n üçün düsturunu ödəyən a, b və c tam ədədlərini tapın(a, b, c>0). Başqa sözlə xn + yn = zn qeyri-müəyyən tənliyinin n≥3 olduqda, heç bir rasiolnal həlli yoxdur. Bu təklif Fermanın böyük və ya sonuncu teoremi adlanır.
İlk baxışdan asan və ya adi görünən bu məsələ təxminən üç əsr yarım dünyanın böyük riyaziyyatçılarına meydan oxumuşdur, onun isbatını riyaziyyatçılar 350 ildən çox axtarmalı olmuşlar. Bu məsələnin həlli Ferma Teoremi (və ya Böyük Ferma Teoremi və ya Son Ferma Teoremi) ilə bağlıdır.
Teoremin mahiyyəti
Teoremdə deyilir: İstənilən tam n>2 üçün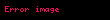 
bərabərliyini ödəyən tam müsbət a, b və c ədədləri tapmaq mümkün deyil.
Deməli, verilən məsələnin həlli yalnız n=1 və n=2 hallarında mümkün ola bilər. Doğrudan da n=1 və n=2 olduqda yuxarıdakı bərabərliyi ödəyən həllər var, hətta belə həllər (yəni bərabərliyi ödəyən müsbət tam a, b və c ədədləri sonsuz saydadır!. Məsələn, n=1 olarsa a və b olaraq istənilən iki tam müsbət ədəd, c olaraq onların cəmini götürmək olar: a=1, b=2, c=3; a=4, b=7, c=11 və s. Doğrudan da 
. n=2 üçün, məsələn. 
. onu da qeyd edək ki, n=2 halında baxılan əsas bərabərliyi ödəyən a, b, c üçlüyünə Pifaqor üçlüyü deyilir.
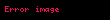
- n>2 üçün isə məsələnin həlli yoxdur.
Bu teorem Pyer Ferma tərəfindən 1637-ci irəli sürülmüşdür və Fermanın şərəfinə Ferma Teoremi adlandırılmışdır. Lakin Ferma öz qeydlərini yazdığı kitabın səhifələrində teoremin isbatını verməmiş, onun uzun olduğu demişdir. "Kubu iki kuba, kvadratın kvadratını iki kvadratın kvadratın, ümumiyyətlə dərcəsi ikidən böyük sonsuzluğa qədər heç bir qüvvəti bütün həmin dərəcəli iki qüvvətə ayırmaq olmaz. Mən bunun həqiqətən çox gözəl isbatını tapmışam, ama onun üçün yer olduqca azdır". Təbii ki, o, bütün n-lər üçün teoremin əsl isbatını bilmirdi. Bu və buna bənzər tənliklər, yəni həlli tam müsbət ədədlər arasında axtarılan tənliklər ilk dəfə Qədim yunan riyaziyyatçısı kitabında daxil edilmişdir.
Teoremin isbatına cəhdlər
Fermanın özü yalnız n=4 halında teoremin isbatını saxlamışdır. Leonard Eyler teoremin n=3 halını isbat etməsindən 30 il keçdikdən sonra bu halı 1738-ci ildə yenidən isbat etdi. 1825-ci ildə isə Lejön-Dirixle və Lejandr tərəfindən teoremin n=5 halı üçün isbatı verilmişdir. Bu teoremlərin hər birinin isbatının hər iki hal üçün olduqca mürəkkəb və uzun olduğunu nəzərə alaraq burada onun isbatlarını vermirik. Ümumiyyətlə, bu halların isbatı üçün tamamilə yeni bir ideya lazım idi ki, bunu da Ferma tapmışdır: bu sonsuz enmə metodudur. Ferma təsdiq etmişdir ki, özünün ədədlərə aid ən məşhur teoremlərini o məhz bu üsulla isbat etmişdir. Enmə üsulu bu gün də ədədlər nəzəriyyəsinə mühüm rol oynayır. Eyler n=3 qiymətində Ferma teoremini 1768-ci ildə isbat etmişdir. Bunun üçün tamamilə yeni bir ideya tələb olumurdu. O, burda çox cəsarətli bir addım atmışdır. Bu ideyanın mahiyyəti adi tam ədədlərə aid məsələlərin tədqiqində a+b
, şəklində olan xəyali ifadələrin tətbiqindən ibarətdir. Eyler öz isbatında α = a+b 
şəklində ifadəyə baxmışdır. Lakin bütün bunlarla və adları sadalanayan məsələlərlə əlaqədar olaraq Eyler öz mülahizəsini əsaslandırmadı və bu məsələlə yenə də Ferma teoreminin isbatı ilə bağlı yenidən XIX əsr riyaziyyatçıları qarşısında dayandı. 1 mart 1847-ci ildə fransız riyaziyyatçısı və fiziki Qabriel Lame Paris Elmlər Akademiyasının iclasında böyük teoremin yeni isbatını məruzə etmişdir. Digrə məşhur farnsız riyaziyyatçısı Liuvill bu barədə yazırdı: "edilən cəhdlər mənə göstərdi ki, əvvəlcə kompleks ədədlər üçün "hasil yalnız bir üsulla sadə vuruqlarına ayrıla bilər" elementar fərxiyyəsinə analoji teoremi müəyyən etmək lazımdır. Lamenin fikri məndə yalnız bu ikri təsdiqlədi, burda doldurulası boşluq yoxdur ki?" Bu qeydlər sayəsində riyaziyyatın bu bölməsi bir ilə yaxın müddətdə fransız riyaziyyatçılarının diqqət mərkəzində oldu. Bu sahə ilə Lamenin özü və digər alimlər intensiv şəkildə məşğul oldular. Onların tədqiqatları nəticəsində tam ədədlərin toplama, vurma və bölməyə nəzərən xassələrini ən ümumi şəklidə ifadə edən yeni bir riyazi obyekt – halqa anlayışı formalaşdı. Həmçinin sonralar alman riyaziyyatçısı Böyük teoremlə məşğul olarkən cəbrə yeni mühüm obyektlər – ideallar daxil etmişdir.
Son cəhdlər
XX əsrin sonu riyaziyyatçılar üçün həqiqi sensasiya ilə əlamətdar oldu. Fermanın böyük teoremini isbat etmək cəhdi, nəhayət ki, müvəffəqiyyətlə nəticələndi. 1995-ci ilin yayında aparıcı riyaziyyat jurnalllarının birində — "Riyaziyyat salnaməsi" jurnalında teoremin tamm isbatı dərc olundu. 100 səhifədən çox həcmə malik olan isbat iki məaqaləyə bölünərək bütün məqaləni tam tuturdu. İsbatın əsas hisəsi təxminən 10 il bu məşhur problem üzərində çalışan Prinston universitetinin professoru 42 yaşlı Endri Wilesə məxsus idi. Son mərhələdə isə Oksford universitetinin professoru Riçard Teylor qoşulmuşdur. O, Uaylsın ilkin isbatında olan boşluğu aradan qaldırmağa kömək etmişdir. Uayls bu ilkin isbatı 1993-cü il 23 iyulda Kembricdə İsaak Nyuton adına Riyaziyyat institutunda oxuduğu mühazirələrində şərh etmişdir. Bu iş gərgin yaradıcı əməyin məhsulu idi. Uaylsın etirafına görə arvadından başqa heç kəs onun bu sahədə işlədiyini bilmirdi. XX əsrdə böyük teoremlə sürətlə inkişaf edən riyazi nəzəriyyəylə cəbri həndəsənin əlaqəsi üzə çıxdı. Məhz bu nəzəriyyə çərçivəsində müvəffəqiyyət əldə olundu. Ferma teoreminin isbatında çoxlu riyaziyyatçıların əməyi olmuşdur. Uaylsın ideyası xn + yn = zn tənliyi və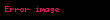 
tənlyi ilə verilən elliptik əyrilər arsındakı çox yaxşı əlaqəyə əsaslanıb. İlk dəfə ona fransız riyaziyyatçısı İv Elleqarş diqqət yetirmişdir. Əvvəllər elliptik əyrilər çoxluğunun modulyarlıq adlanan bir xassəsi hipoteza şəklində yapon riyaziyyatçısı ifadə etmişdi. 1985-ci ildə alman alimi Herxard Fery, əyriləri üçün doğru olan hipotezdən Ferma teoremini almağın mümkünlüyünün ideyasını təklif etdi. Sonralar amerika alimləri onun fərziyyəsini təsdiq etdi. Beləliklə, Ferma teoremini isbat etmək üçün yalnız Yapon alminin hipotezinin isbatını tapmaq qalırdı. Məhz bu Uayls tərəfindən Kembric mühaizrlərində şərh edilmişdir. Belə hünəri heç kim kifayət qədər az tanınan riyaziyyatçıdan gözləmirdi. Mütəxəssilər Uaylsın verdiyi isbatı diqqətlə yoxlamağa başladılar. Bir neçə aydan sonra onlar Uaylsın işlərində boşluq tapdılar. Ümumilikdə isə onun ideyalarının müasirliyi, dərinliyi və gözəlliyi təsdiq olundu. Uayls isbatı düzəltmək qərarına gəldi. Bir ilə yaxın vaxt keçdikdən sonra onu keçirilən riyaziyyat üzrə növbəti Beynəlxalq Konqresə dəvət etdilər. Bütün riyaziyyat aləmi onun məruzəsini, əlbəttə ki, səbirsizliklə gözləyirdilər. Təbii ki, Uayls isbatı çıxış növbəsinə kimi tamamalamaq istəyirdi, amma o, buna müvəffəq olmadı. Həmkarları onu məruzədən əvvəl auditoriyanın yanındakı pilləkənlərdə oturub necə işlədiyinin şahidi oldular. Uayls kafedraya qalxarkən onu donmuş vəziyyətdə gözləyən zala isbatı tam yerinə yetirmədiyi xəbərini verdi. Zal onu dostcasına alqışladı. Artıq konqresdən bir ay sonra Uaylsın özünün sözlərinə görə əsas ideyası işıqlandı və yaranmış boşluğu nəhayət ki doldura bildi. Bu dəfə isabt son dərəcə dəqiq yoxlanmalara davam gətirdi və çap olundu.
Həmçinin bax
Xarici keçidlər
- Wiles, Andrew (1995). Modular elliptic curves and Fermat's last theorem 2011-05-10 at the Wayback Machine, Annals of Mathematics (141) (3), 443–551.
- Taylor, Richard & Wiles, Andrew (1995). Ring theoretic properties of certain Hecke algebras 2001-11-27 at the Wayback Machine, Annals of Mathematics (141) (3), 553–572.
- Faltings, Gerd (1995). The Proof of Fermat's last theorem by R. Taylor and A. Wiles, Notices of the AMS (42) (7), 743–746.
- Daney, Charles (2003). The Mathematics of Fermat's last theorem 2004-08-03 at the Wayback Machine. Retrieved Aug. 5, 2004.
- O'Connor, J. J. & and Robertson, E. F. (1996). Fermat's last theorem. The history of the problem 2004-08-04 at the Wayback Machine. Retrieved Aug. 5, 2004.
- Shay, David (2003). Fermat's last theorem. The story, the history and the mystery. Retrieved Aug. 5, 2004.
- The Moment of Proof : Mathematical Epophanies, by ; Oxford University Press; (paperback, 1999)
- С. Сингх, Великая теорема Ферма, М. МЦНМО, 2000.
- Freeman, Larry (2005). Fermat's Last Theorem Blog. A blog that covers the history of Fermat's Last Theorem from Pierre Fermat to Andrew Wiles.
- Kisby, Adam William (2004). Fermat's Last Theorem Revisited: A Marginal Proof in Ten Steps 2005-12-16 at the Wayback Machine. Parody.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqaleni vikilesdirmek lazimdir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Bu teoremi Hesab kitabinin ikinci hissesinde 8 ci meselenin qarsisinda yazmisdi Verilen kvadarti iki kvadrata ayirin Basqa sozle desek verilmis a ededi ucun x2 y2 a2 tenliyini rasional hellerini tapmaq teleb olunur Bu da ki bizlere cox yaxsi tanis olan Pifaqor teoremidir ve onun sonsuz sayda helli var Ferma qeyd etmisdir Kubu iki kuba kvadratin kvadratini iki kvadratin kvadratina umumiyyetle derecesi ikiden boyuk sonsuzluga qeder hec bir quvveti butun hemin dereceli iki quvvete ayirmaq olmaz Men bunun heqiqeten cox gozel isbatini tapmisam ama onun ucun yer olduqca azdir Tutaq ki bize bele bir mesele verilib Verilmis tam musbet n ucun an bn cn displaystyle a n b n c n dusturunu odeyen a b ve c tam ededlerini tapin a b c gt 0 Basqa sozle xn yn zn qeyri mueyyen tenliyinin n 3 olduqda hec bir rasiolnal helli yoxdur Bu teklif Fermanin boyuk ve ya sonuncu teoremi adlanir Pyer Ferma Ilk baxisdan asan ve ya adi gorunen bu mesele texminen uc esr yarim dunyanin boyuk riyaziyyatcilarina meydan oxumusdur onun isbatini riyaziyyatcilar 350 ilden cox axtarmali olmuslar Bu meselenin helli Ferma Teoremi ve ya Boyuk Ferma Teoremi ve ya Son Ferma Teoremi ile baglidir Teoremin mahiyyetiTeoremde deyilir Istenilen tam n gt 2 ucun an bn cn displaystyle a n b n c n beraberliyini odeyen tam musbet a b ve c ededleri tapmaq mumkun deyil Demeli verilen meselenin helli yalniz n 1 ve n 2 hallarinda mumkun ola biler Dogrudan da n 1 ve n 2 olduqda yuxaridaki beraberliyi odeyen heller var hetta bele heller yeni beraberliyi odeyen musbet tam a b ve c ededleri sonsuz saydadir Meselen n 1 olarsa a ve b olaraq istenilen iki tam musbet eded c olaraq onlarin cemini goturmek olar a 1 b 2 c 3 a 4 b 7 c 11 ve s Dogrudan da 11 21 31 displaystyle 1 1 2 1 3 1 n 2 ucun meselen 32 42 52 displaystyle 3 2 4 2 5 2 onu da qeyd edek ki n 2 halinda baxilan esas beraberliyi odeyen a b c ucluyune Pifaqor ucluyu deyilir n gt 2 ucun ise meselenin helli yoxdur Bu teorem Pyer Ferma terefinden 1637 ci ireli surulmusdur ve Fermanin serefine Ferma Teoremi adlandirilmisdir Lakin Ferma oz qeydlerini yazdigi kitabin sehifelerinde teoremin isbatini vermemis onun uzun oldugu demisdir Kubu iki kuba kvadratin kvadratini iki kvadratin kvadratin umumiyyetle dercesi ikiden boyuk sonsuzluga qeder hec bir quvveti butun hemin dereceli iki quvvete ayirmaq olmaz Men bunun heqiqeten cox gozel isbatini tapmisam ama onun ucun yer olduqca azdir Tebii ki o butun n ler ucun teoremin esl isbatini bilmirdi Bu ve buna benzer tenlikler yeni helli tam musbet ededler arasinda axtarilan tenlikler ilk defe Qedim yunan riyaziyyatcisi kitabinda daxil edilmisdir Teoremin isbatina cehdlerFermanin ozu yalniz n 4 halinda teoremin isbatini saxlamisdir Leonard Eyler teoremin n 3 halini isbat etmesinden 30 il kecdikden sonra bu hali 1738 ci ilde yeniden isbat etdi 1825 ci ilde ise Lejon Dirixle ve Lejandr terefinden teoremin n 5 hali ucun isbati verilmisdir Bu teoremlerin her birinin isbatinin her iki hal ucun olduqca murekkeb ve uzun oldugunu nezere alaraq burada onun isbatlarini vermirik Umumiyyetle bu hallarin isbati ucun tamamile yeni bir ideya lazim idi ki bunu da Ferma tapmisdir bu sonsuz enme metodudur Ferma tesdiq etmisdir ki ozunun ededlere aid en meshur teoremlerini o mehz bu usulla isbat etmisdir Enme usulu bu gun de ededler nezeriyyesine muhum rol oynayir Eyler n 3 qiymetinde Ferma teoremini 1768 ci ilde isbat etmisdir Bunun ucun tamamile yeni bir ideya teleb olumurdu O burda cox cesaretli bir addim atmisdir Bu ideyanin mahiyyeti adi tam ededlere aid meselelerin tedqiqinde a b n displaystyle scriptstyle sqrt n seklinde olan xeyali ifadelerin tetbiqinden ibaretdir Eyler oz isbatinda a a b 3 displaystyle sqrt 3 seklinde ifadeye baxmisdir Lakin butun bunlarla ve adlari sadalanayan meselelerle elaqedar olaraq Eyler oz mulahizesini esaslandirmadi ve bu meselele yene de Ferma teoreminin isbati ile bagli yeniden XIX esr riyaziyyatcilari qarsisinda dayandi 1 mart 1847 ci ilde fransiz riyaziyyatcisi ve fiziki Qabriel Lame Paris Elmler Akademiyasinin iclasinda boyuk teoremin yeni isbatini meruze etmisdir Digre meshur farnsiz riyaziyyatcisi Liuvill bu barede yazirdi edilen cehdler mene gosterdi ki evvelce kompleks ededler ucun hasil yalniz bir usulla sade vuruqlarina ayrila biler elementar ferxiyyesine analoji teoremi mueyyen etmek lazimdir Lamenin fikri mende yalniz bu ikri tesdiqledi burda doldurulasi bosluq yoxdur ki Bu qeydler sayesinde riyaziyyatin bu bolmesi bir ile yaxin muddetde fransiz riyaziyyatcilarinin diqqet merkezinde oldu Bu sahe ile Lamenin ozu ve diger alimler intensiv sekilde mesgul oldular Onlarin tedqiqatlari neticesinde tam ededlerin toplama vurma ve bolmeye nezeren xasselerini en umumi seklide ifade eden yeni bir riyazi obyekt halqa anlayisi formalasdi Hemcinin sonralar alman riyaziyyatcisi Boyuk teoremle mesgul olarken cebre yeni muhum obyektler ideallar daxil etmisdir Son cehdler XX esrin sonu riyaziyyatcilar ucun heqiqi sensasiya ile elametdar oldu Fermanin boyuk teoremini isbat etmek cehdi nehayet ki muveffeqiyyetle neticelendi 1995 ci ilin yayinda aparici riyaziyyat jurnalllarinin birinde Riyaziyyat salnamesi jurnalinda teoremin tamm isbati derc olundu 100 sehifeden cox hecme malik olan isbat iki meaqaleye bolunerek butun meqaleni tam tuturdu Isbatin esas hisesi texminen 10 il bu meshur problem uzerinde calisan Prinston universitetinin professoru 42 yasli Endri Wilese mexsus idi Son merhelede ise Oksford universitetinin professoru Ricard Teylor qosulmusdur O Uaylsin ilkin isbatinda olan boslugu aradan qaldirmaga komek etmisdir Uayls bu ilkin isbati 1993 cu il 23 iyulda Kembricde Isaak Nyuton adina Riyaziyyat institutunda oxudugu muhazirelerinde serh etmisdir Bu is gergin yaradici emeyin mehsulu idi Uaylsin etirafina gore arvadindan basqa hec kes onun bu sahede islediyini bilmirdi XX esrde boyuk teoremle suretle inkisaf eden riyazi nezeriyyeyle cebri hendesenin elaqesi uze cixdi Mehz bu nezeriyye cercivesinde muveffeqiyyet elde olundu Ferma teoreminin isbatinda coxlu riyaziyyatcilarin emeyi olmusdur Uaylsin ideyasi xn yn zn tenliyi ve y2 x x an x cn displaystyle y 2 x x a n x c n tenlyi ile verilen elliptik eyriler arsindaki cox yaxsi elaqeye esaslanib Ilk defe ona fransiz riyaziyyatcisi Iv Elleqars diqqet yetirmisdir Evveller elliptik eyriler coxlugunun modulyarliq adlanan bir xassesi hipoteza seklinde yapon riyaziyyatcisi ifade etmisdi 1985 ci ilde alman alimi Herxard Fery y2 x x an x cn displaystyle y 2 x x a n x c n eyrileri ucun dogru olan hipotezden Ferma teoremini almagin mumkunluyunun ideyasini teklif etdi Sonralar amerika alimleri onun ferziyyesini tesdiq etdi Belelikle Ferma teoremini isbat etmek ucun yalniz Yapon alminin hipotezinin isbatini tapmaq qalirdi Mehz bu Uayls terefinden Kembric muhaizrlerinde serh edilmisdir Bele huneri hec kim kifayet qeder az taninan riyaziyyatcidan gozlemirdi Mutexessiler Uaylsin verdiyi isbati diqqetle yoxlamaga basladilar Bir nece aydan sonra onlar Uaylsin islerinde bosluq tapdilar Umumilikde ise onun ideyalarinin muasirliyi derinliyi ve gozelliyi tesdiq olundu Uayls isbati duzeltmek qerarina geldi Bir ile yaxin vaxt kecdikden sonra onu kecirilen riyaziyyat uzre novbeti Beynelxalq Konqrese devet etdiler Butun riyaziyyat alemi onun meruzesini elbette ki sebirsizlikle gozleyirdiler Tebii ki Uayls isbati cixis novbesine kimi tamamalamaq isteyirdi amma o buna muveffeq olmadi Hemkarlari onu meruzeden evvel auditoriyanin yanindaki pillekenlerde oturub nece islediyinin sahidi oldular Uayls kafedraya qalxarken onu donmus veziyyetde gozleyen zala isbati tam yerine yetirmediyi xeberini verdi Zal onu dostcasina alqisladi Artiq konqresden bir ay sonra Uaylsin ozunun sozlerine gore esas ideyasi isiqlandi ve yaranmis boslugu nehayet ki doldura bildi Bu defe isabt son derece deqiq yoxlanmalara davam getirdi ve cap olundu Hemcinin baxFerma noqtesiXarici kecidlerWiles Andrew 1995 Modular elliptic curves and Fermat s last theorem 2011 05 10 at the Wayback Machine Annals of Mathematics 141 3 443 551 Taylor Richard amp Wiles Andrew 1995 Ring theoretic properties of certain Hecke algebras 2001 11 27 at the Wayback Machine Annals of Mathematics 141 3 553 572 Faltings Gerd 1995 The Proof of Fermat s last theorem by R Taylor and A Wiles Notices of the AMS 42 7 743 746 Daney Charles 2003 The Mathematics of Fermat s last theorem 2004 08 03 at the Wayback Machine Retrieved Aug 5 2004 O Connor J J amp and Robertson E F 1996 Fermat s last theorem The history of the problem 2004 08 04 at the Wayback Machine Retrieved Aug 5 2004 Shay David 2003 Fermat s last theorem The story the history and the mystery Retrieved Aug 5 2004 The Moment of Proof Mathematical Epophanies by Oxford University Press ISBN 0 19 513919 4 paperback 1999 S Singh Velikaya teorema Ferma M MCNMO 2000 Freeman Larry 2005 Fermat s Last Theorem Blog A blog that covers the history of Fermat s Last Theorem from Pierre Fermat to Andrew Wiles Kisby Adam William 2004 Fermat s Last Theorem Revisited A Marginal Proof in Ten Steps 2005 12 16 at the Wayback Machine Parody