Vin qanunu (yerdəyişmə qanunu) — mütləq qara cismin şüalanma spektrində enerjinin temperaturdan asılı olaraq paylanması qanunu.

Vilhelm Vin bu qanunu ilk dəfə 1893-cü ildə termodinamika qanunlarını elektromaqnit şüalanmasına tətbiq etməklə çıxarmışdır. İntensivlik pikinin temperatura nəzərən yerdəyişməsi təcrübi olaraq müşahidə edilmişdir. Hal-hazırda, Vinin yerdəyişmə qanunu riyazi olaraq Plank qanunundan əldə etmək mümkündür.
Vinin yerdəyişmə qanununun ümumi şəkli
Qanun aşağıdakı düsturla ifadə edilir:

burada 
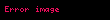



İşığın tezliyi üçün (herslə) Vinin yerdəyişmə qanunu aşağıdakı formada olar:

α≈ 2,821439… — sabit kəmiyyət (



Qanunun çıxarılışı
Çıxarılış üçün mütləq qara cismin şüalanma qabiliyyəti 

Dalğa uzunluğundan asılı olaraq bu funksiyanın ekstremumunu tapmaq üçün onun 

Bu düsturdan dərhal müəyyən etmək olar ki, 






Bu tənliyin ədədi həlli aşağıdakı kimidir

Beləliklə, əvəzetmədən, Plank və Bolsman sabitlərinin qiymətlərindən və işıq sürətindən istifadə edərək, qara cismin şüalanma intensivliyinin maksimuma çatdığı dalğa uzunluğunu müəyyən edə bilərik:

burada 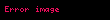

Nümunələr
Vinin yerdəyişmə qanununa görə, insanın bədən temperaturuna (~310 K) malik qara cisim, spektrin infraqırmızı diapazonuna uyğun gələn təxminən 10 mkm dalğa uzunluğunda maksimum istilik şüalanmasına malikdir.
Qalıq şüalanmanın effektiv temperaturu 2,7 K və 1 mm dalğa uzunluğunda maksimuma çatır. Müvafiq olaraq, bu dalğa uzunluğu artıq radio diapazonuna aiddir.
Qeydlər
-
tənliyinin həlli elementar funksiyaların köməyilə ifadə edilə bilməz. Onun dəqiq həllini Lambert W-funksiyasından istifadə etməklə tapmaq olar, lakin bu halda təqribi həlldən istifadə etmək kifayətdir.
Ədəbiyyatlar
- Erik Veyşteynin fizika dünyası (ing.)
- Soffer, B. H.; Lynch, D. K. Some paradoxes, errors, and resolutions concerning the spectral optimization of human vision (ing.) // American Journal of Physics: journal. — 1999. — Vol. 67, no. 11. — P. 946–953. — doi:10.1119/1.19170. — Bibcode: 1999AmJPh..67..946S.
- Heald, M. A. Where is the 'Wien peak'? (ing.) // American Journal of Physics. — 2003. — Vol. 71, no. 12. — P. 1322–1323. — doi:10.1119/1.1604387. — Bibcode: 2003AmJPh..71.1322H.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Vin qanunu yerdeyisme qanunu mutleq qara cismin sualanma spektrinde enerjinin temperaturdan asili olaraq paylanmasi qanunu Muxtelif temperaturlar ucun dalga uzunlugundan asili olaraq mutleq qara cismin sualanmasi Her bir temperatur eyrisi ferqli dalga uzunlugunda maksimuma catir ve Vin qanunu hemin maksimumun yerdeyismesini tesvir edir Vilhelm Vin bu qanunu ilk defe 1893 cu ilde termodinamika qanunlarini elektromaqnit sualanmasina tetbiq etmekle cixarmisdir Intensivlik pikinin temperatura nezeren yerdeyismesi tecrubi olaraq musahide edilmisdir Hal hazirda Vinin yerdeyisme qanunu riyazi olaraq Plank qanunundan elde etmek mumkundur Vinin yerdeyisme qanununun umumi sekliQanun asagidaki dusturla ifade edilir lmax bT displaystyle lambda text max frac b T burada lmax displaystyle lambda text max maksimum intensivlikli sualanmanin dalga uzunlugu T displaystyle T mutleq temperatur b displaystyle b ise mutenasiblik emsali olub Vin sabiti adlanir Mutenasiblik emsali b chka displaystyle b frac ch k alpha burada c isigin vakuumdaki sureti h Plank sabiti k Bolsman sabiti a 4 965114 ise sabit kemiyyet olub a 5 1 e a displaystyle alpha 5 1 e alpha tenliyinin kokudur Vin sabitinin Beynelxalq Vahidler Sistemindeki BS qiymeti 2898 mkm K dir Isigin tezliyi ucun hersle Vinin yerdeyisme qanunu asagidaki formada olar nmax ahkT 5 879 1010 T displaystyle nu text max frac alpha h kT approx 5 879 times 10 10 cdot T a 2 821439 sabit kemiyyet a 3 1 e a displaystyle alpha 3 1 e alpha tenliyinin koku k Bolsman sabiti h Plank sabiti T ise mutleq temperaturdur Buradaki ededi sabitlerin ferqi sualanmanin dalga uzunlugu ve tezliyi ucun yazilmis Plank paylanmasindaki eksponentler arasindaki ferqle baglidir bir halda l 5 displaystyle lambda 5 diger halda ise w3 l 3 displaystyle omega 3 sim lambda 3 daxildir Bu ferq oz novbesinde tezlik ve dalga uzunlugu arasindaki elaqenin qeyri xetti olmasindan ireli gelir w 2pcl ddw l22pcddl displaystyle omega frac 2 pi c lambda quad frac d d omega frac lambda 2 2 pi c frac d d lambda Qanunun cixarilisiCixarilis ucun mutleq qara cismin sualanma qabiliyyeti el l T displaystyle varepsilon lambda lambda T ucun Plank qanununun ifadesinden istifade etmek olar el 2phc2l51ehc lkT 1 displaystyle varepsilon lambda frac 2 pi hc 2 lambda 5 frac 1 e hc lambda kT 1 Dalga uzunlugundan asili olaraq bu funksiyanin ekstremumunu tapmaq ucun onun l displaystyle lambda deyisenine nezeren toremesini almaq ve hemin toremeni sifira beraberlesdirmek lazimdir el l 2phc2l61ehc lkT 1 hckTlehc lkT ehc lkT 1 5 0 displaystyle frac partial varepsilon lambda partial lambda frac 2 pi hc 2 lambda 6 frac 1 e hc lambda kT 1 left frac hc kT lambda frac e hc lambda kT left e hc lambda kT 1 right 5 right 0 Bu dusturdan derhal mueyyen etmek olar ki l displaystyle lambda to infty ve ya ehc lkT displaystyle e hc lambda kT to infty olduqda toreme sifira yaxinlasir bu l 0 displaystyle lambda to 0 ucun dogrudur Lakin bu hallarin her ikisi B l displaystyle B lambda Plank funksiyasinin minimumunu verir verilmis dalga uzunluqlari ucun sifira catir yuxaridaki sekile bax Buna gore de analiz yalniz ucuncu mumkun halda davam etdirilmelidir hckTlehc lkT ehc lkT 1 5 0 displaystyle frac hc kT lambda frac e hc lambda kT left e hc lambda kT 1 right 5 0 x hckTl displaystyle displaystyle x frac hc kT lambda evezlemesinden istifade etmekle bu tenliyi asagidaki formaya cevirmek olar xexex 1 5 0 displaystyle frac xe x e x 1 5 0 Bu tenliyin ededi helli asagidaki kimidir x 4 965114231744276 displaystyle x 4 965114231744276 ldots Belelikle evezetmeden Plank ve Bolsman sabitlerinin qiymetlerinden ve isiq suretinden istifade ederek qara cismin sualanma intensivliyinin maksimuma catdigi dalga uzunlugunu mueyyen ede bilerik lmax hcx1kT 2 89776829 10 3T displaystyle lambda text max frac hc x frac 1 kT frac 2 89776829 ldots times 10 3 T burada T displaystyle T kelvinle lmax displaystyle lambda text max ise metrle verilmisdir NumunelerVinin yerdeyisme qanununa gore insanin beden temperaturuna 310 K malik qara cisim spektrin infraqirmizi diapazonuna uygun gelen texminen 10 mkm dalga uzunlugunda maksimum istilik sualanmasina malikdir Qaliq sualanmanin effektiv temperaturu 2 7 K ve 1 mm dalga uzunlugunda maksimuma catir Muvafiq olaraq bu dalga uzunlugu artiq radio diapazonuna aiddir Qeydlerxexex 1 n displaystyle frac xe x e x 1 n tenliyinin helli elementar funksiyalarin komeyile ifade edile bilmez Onun deqiq hellini Lambert W funksiyasindan istifade etmekle tapmaq olar lakin bu halda teqribi hellden istifade etmek kifayetdir EdebiyyatlarErik Veysteynin fizika dunyasi ing Soffer B H Lynch D K Some paradoxes errors and resolutions concerning the spectral optimization of human vision ing American Journal of Physics journal 1999 Vol 67 no 11 P 946 953 doi 10 1119 1 19170 Bibcode 1999AmJPh 67 946S Heald M A Where is the Wien peak ing American Journal of Physics 2003 Vol 71 no 12 P 1322 1323 doi 10 1119 1 1604387 Bibcode 2003AmJPh 71 1322H
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська
