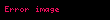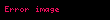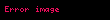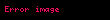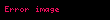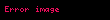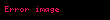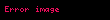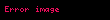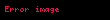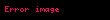Limit (lat. Limes - uc nöqtə) — funksiyanın limiti cəbr analizinin əsas anlayışlarından biridir. İlk dəfə yunan filosofları Arximed və Evklidin əsərlərində rast gəlinir. Müasir riyaziyyatda isə ingilis alimi İsaak Nyuton tərəfindən işlədilmişdir.

Əsas limitlər
Limitin bəzi xassələri
bn ≠ 0 və 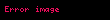
c = const.
с1 = const, c2 = const.
b > 0, a > 0, b ≠ 1 şərtilə.
а > 0 p olduqda
Xarici keçidlər
- Mathwords: Limit
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Limit lat Limes uc noqte funksiyanin limiti cebr analizinin esas anlayislarindan biridir Ilk defe yunan filosoflari Arximed ve Evklidin eserlerinde rast gelinir Muasir riyaziyyatda ise ingilis alimi Isaak Nyuton terefinden isledilmisdir Arqumentde sonsuzluga yaxinlasan limtin qrafiki beraberdir L displaystyle L Esas limitlerlimx 1 1x x e displaystyle lim x to infty 1 frac 1 x x e limx 0 1 x kx ek k 1 x displaystyle lim x to 0 1 x frac k x e k k 1 x limx 0cos x 1 displaystyle lim x to 0 cos x 1 limx 0tan x x 1 displaystyle lim x to 0 frac tan x x 1 Limitin bezi xasselerilimn an bn limn an limn bn displaystyle lim n to infty a n b n lim n to infty a n lim n to infty b n limn an bn limn an limn bn displaystyle lim n to infty a n b n lim n to infty a n lim n to infty b n limn an bn limn an limn bn displaystyle lim n to infty a n b n lim n to infty a n lim n to infty b n limn anbn limn anlimn bn displaystyle lim n to infty frac a n b n frac lim n to infty a n lim n to infty b n bn 0 ve limn bn displaystyle lim n to infty b n 0 limn can climn an displaystyle lim n to infty ca n c lim n to infty a n c const limn c1an c2bn c1limn an c2limn bn displaystyle lim n to infty c 1 a n c 2 b n c 1 lim n to infty a n c 2 lim n to infty b n s1 const c2 const limn logb an logba displaystyle lim n to infty log b a n log b a b gt 0 a gt 0 b 1 sertile limn anp ap displaystyle lim n to infty a n p a p a gt 0 p olduqdaXarici kecidlerMathwords Limit
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans