Eynşteyn sahə tənlikləri

Eynşteyn sahə tənlikləri — qravitasiyanın, əslində fəza-zamanın kütlə və enerji tərəfindən əyilməsi ilə meydana çıxan anlayış olduğunu riyazi şəkildə göstərən 10 ibarət sistemdir. Eynşteyn tenzoru ilə ifadə olunan fəzazamandakı lokal əyriliyi həmin sahədə yerləşən və gərginlik-enerji tenzoru ilə ifadə olunan maddə ilə əlaqələndirən bu tənliklər, 1915-ci ildə Albert Eynşteyn tərəfindən Ümumi Nisbilik Nəzəriyyəsində irəli sürülmüşdür. 

Sahə tənlikləri bu formada olub,

$${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }}$$

${\displaystyle G_{\mu \nu }}$ — Eynşteyn tenzorunu,

${\displaystyle \Lambda }$ — Kosmoloji sabiti,

${\displaystyle g_{\mu \nu }}$ — metrik tenzoru

${\displaystyle T_{\mu \nu }}$ — ,

${\displaystyle G}$ və ${\displaystyle c}$ isə uyğun olaraq Qravitasiya Sabiti və işıq sürətini

göstərir.

Beləcə 4 ölçülü fəza-zamanda hər ${\displaystyle \mu }$ və ${\displaystyle \nu }$ komponenti üçün 4 tənlik olmaqla cəmi 16 tənlik olmalıdır. Lakin tənlikdəki bütün tenzorlar simmetrik olduğundan(${\displaystyle X_{\mu \nu }=X_{\nu \mu }}$) eynicinsli tənlikləri çıxmaqla bir-birindən ayrı 10 tənlik qalır.

Eyşteyn tenzoru

Eynşteyn tenzoru 2 indeksi üzrə cəmlənməsindən(${\displaystyle R_{\mu \nu }=R_{\;\mu \lambda \nu }^{\lambda }}$) əmələ gələn üzərində qurulur və enerji-impuls tenzoru ilə mütənasib olub fəza-zaman əyriliyini xarakterizə edən tenzor olaraq Eynşteyn tərəfindən gətirilib:

${\displaystyle G_{\mu \nu }=R_{\mu \nu }-{\tfrac {1}{2}}R\,g_{\mu \nu },}$

burada

${\displaystyle R_{\mu \nu }}$ — Rikki tenzoru,

${\displaystyle R}$ — Rikki skalyarıdır(${\displaystyle R=R_{\alpha \beta }g^{\alpha \beta }}$).

Eynşteyn tenzorunun Rikki tenzorundan əsas fərqləndirici xüsusiyyəti, onun gərginlik-enerji tenzoru kimi konservativ olmasıdır:

${\displaystyle \nabla ^{\mu }{G_{\mu \nu }}=0}$.

Eynşteyn tenzorunun açılışını nəzərə alsaq, sahə tənlikləri

$${\displaystyle R_{\mu \nu }-{1 \over 2}R\,g_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }}$$

şəklində ifadə olunar.

Kosmoloji sabit

Sahə tənlikləri ilk dəfə kosmoloji sabit faktoru olmadan, bu şəkildə yazılmışdı:

${\displaystyle G_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }.}$

Daha sonra Eynşteyn, Ümumi Nisbilik Nəzəriyyəsini kainatı modelləşdirmək üçün tətbiq etdikdə mövcud tənliklər, kainatın ya daima genişlənəcəyinə, ya da tək bir sinqulyar nöqtəyə çökməli olduğuna dəlalət edirdi. Eynşteynsə nəzəriyyəni özünün modelinə uyğunlaşdırmaq üçün sahə tənliklərinə kosmoloji sabit faktorunu(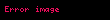${\displaystyle \Lambda g_{\mu \nu }}$) əlavə etdi. Sonralar Edvin Hubble kainatın genişlənməsini kəşf etdikdə Eynşteyn kosmoloji sabiti özünün "ən böyük axmaqlığı" adlandırdı və tənliklərdən çıxardı.

Buna baxmayaraq illər sonra kainatın genişlənməsinin ilə bağlı olması iddiaları ortaya atılanda kosmoloji sabit sahə tənliklərinə yenidən əlavə edilməli oldu.

Gərginlik-enerji tenzoru

Gərginlik-enerji tenzoru, gərginlik tenzorunun 4 ölçülü fəza-zaman üçün ümumiləşdirilməsidir. Simmetrik tenzor olduğundan 10 sərbəst komponenti var. Gərginlik-enerji tenzoru ikinci tərtib tenzor olub komponentləri matriks şəklində ifadə olunur.

Gərginlik-enerji tenzoru komponentlərində maddə ilə bağlı nisbi xassələri(enerji, impuls, sıxlıq, təzyiq) cəmləşdirərək koordinat sistemindən asılı olmayan kəmiyyət(tenzor) formalaşdırır.

İdeal maye üçün gərginlik-enerji tenzoru

$${\displaystyle T^{\alpha \beta }=(\rho +{\frac {p}{c^{2}}})U^{\alpha }U^{\beta }+pg^{\alpha \beta }}$$

şəkildə ifadə olunur. Burada,

${\displaystyle \rho }$ —enerji sıxlığı

${\displaystyle p}$—mayenin təzyiqi

${\displaystyle U^{\alpha }}$və ${\displaystyle U^{\beta }}$ mayenin fəza-zamanda komponentləridir.

${\displaystyle g^{\alpha \beta }}$—tərs metrikadır(${\displaystyle g^{\alpha \beta }={\frac {1}{g_{\alpha \beta }}}}$).

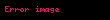
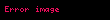
Gərginlik-enerji tenzorunu alt indekslərlə ifadə etmək istəsək(sahə tənliklərində olduğu kimi)

${\displaystyle T_{\mu \nu }=g_{\mu \alpha }g_{\nu \beta }T^{\alpha \beta }}$

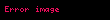
şəklində çevirmə etməli olarıq.

Nyuton qravitasiyası ilə uyğunluğu

Ümumi nisbilik nəzəriyyəsinə qədər qravitasiya Nyutonun Ümumdünya Cazibə Qanunu ilə izah olunurdu, bu qanundan çıxan düsturlar müəyyən dərəcəyə qədər dəqiq nəticələr verirdi. Lakin çox böyük kütləli cisimlərin(qara dəlik, , qalaktikalar və s.) hərəkəti və qravitasiya təbiəti ilə bağlı təxminlər verğ bilmirdi. Ümumi nisbilik nəzəriyyəsi isə qravitasiyanın təsirinə bir qüvvə kimi deyil, cisimlərin öz təbii hərəkət(düzxəttli bərabərsürətli) yolunun, fəza-zamanın əyilməsi nəticəsində dəyişilməsi kimi yanaşırdı. Nəticə etibarilə bu nəzəriyyə demək olar ki, kainatdakı bütün cisimlərin hərəkətini çox dəqiqliklə təsvir edə bilirdi.

Ümumi nisbilik nəzəriyyəsinin doğru olması üçün bu nəzəriyyə müəyyən limitlərdə Nyuton qravitasiyası ilə eyniləşməlidir, çünki bu limitlərdə Nyuton qravitasiyasının düzgün nəticələr verməsi onun yanlış nəzəriyyə deyil, natamam nəzəriyyə olduğunu göstərir. Bu baxımdan da Eynşteyn qravitasiyası Nyuton qravitasiyasından fərqli nəzəriyyə deyil, onu daha böyük limitlərdə tamamlayan nəzəriyyə olmalıdır.

Nyuton qravitasiyasında cismin yaratdığı qravitasiya sahəsinin potensialı ilə müəyyən olunur,

${\displaystyle \nabla ^{2}{\Phi }=4\pi G\rho }$ .

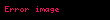
Nyuton limitlərini Ümumi Nisbilik Nəzəriyyəsində nəzərə aldıqda Eynşteyn sahə tənlikləri Poisson tənlikləri, Poisson sahə tənliklərinə çevrilməlidir.

Cismin qravitasiya sahəsində aldığı təcil sahə potensialının ilə düz mütənasibdir:

${\displaystyle a=-\nabla \Phi }$.

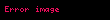
Nyuton qravitasiyası bu limitləri nəzərə alır:

1. Cisimlər işıq sürətindən çox-çox kiçik sürətlərdə hərəkət edir, işıq sonsuz böyük sürətlə hərəkət edir
   $${\displaystyle v\ll c,\quad c\to \infty }$$
2. Hesablamalar zəif qravitasiya sahəsində tətbiq olunur, belə sahədə fəza-zamanın metrikası çox yaxındır və bu metrikayla çox kiçik metrikanın cəmi şəklində göstərilə bilər
   $${\displaystyle g_{\mu \nu }=\eta _{\mu \nu }+h_{\mu \nu },\quad |h_{\mu \nu }|\ll 1}$$
3. Qravitasiya sahəsi zaman keçdikcə dəyişmir, statikdir, bunu ÜNN dili ilə desək, çoxobrazlıda təyin olunan metrikanın zamana görə törəməsi sıfıra bərabərdir.
   $${\displaystyle {\frac {\partial {g_{\mu \nu }}}{\partial t}}=0}$$

Enerji vəziyyətləri

Eynşteyn tənlikləri fəza-zamandakı istənilən növ enerjinin həmin fəza-zamanda lokal olaraq necə əyrilik yaratdığını ifadə edir. Bu tənliklərdən həmçinin istənilən fəza-zaman əyriliyini yaratmaq üçün hansı tərkibdə enerjinin lazım olmasını öyrənmək olar. Bunun üçün arzuolunan əyriliyə xas Eynşteyn tenzorunu yerinə yazıb tənlikləri enerji-impuls tenzoruna görə həll etmək kifayətdir. Amma təbiətdə enerji istənilən formada mövcud ola bilməz. Məsələn, tənliklərdən çıxan nəticə enerji-impuls tenzorunda enerji sıxlığının mənfi olmasını tələb edə bilər, amma mənfi enerji kainatda ola bilməz(əks halda boş vakuum mənfi və müsbət enerjili sahələrə parçalanardı). Eynşteyn tənlikləri enerji və fəza-zaman arasındakı əlaqəni çox geniş miqyasda ifadə etsə də qeyri-fiziki nəticələri çıxdaş etmir.

Enerji-impuls tenzoruna uyğun məhdudiyyətlər qoymaqla qeyri-fiziki nəticələri çıxdaş etmək üçün müxtəlif enerji vəziyyətləri nəzərə alınır. Bunlar aşağıdakılardır:

1. Zəif enerji vəziyyəti—istənilən zamanşəkilli ${\displaystyle t^{\mu }}$ vektoru üçün ${\displaystyle T_{\mu \nu }t^{\mu }t^{\nu }\geq 0}$. İdeal maye üçün bu, ${\displaystyle \rho \geq 0}$ və ${\displaystyle \rho +{\frac {p}{c^{2}}}\geq 0}$ şərtlərinin ödənməsi deməkdir.
2. Sıfır enerji vəziyyəti—istənilən ${\displaystyle l^{\mu }}$ üçün ${\displaystyle T_{\mu \nu }l^{\mu }l^{\nu }\geq 0}$. İdeal maye üçün bu, ${\displaystyle \rho +{\frac {p}{c^{2}}}\geq 0}$ şərtinin ödənməsi deməkdir.
3. Dominant enerji vəziyyəti—istənilən zamanşəkilli ${\displaystyle t^{\mu }}$ vektoru üçün ${\displaystyle T_{\mu \nu }t^{\mu }t^{\nu }\geq 0}$ olmaqla yanaşı ${\displaystyle T^{\mu \nu }t_{\mu }}$ vektoru fəzaşəkilli deyil. İdeal maye üçün bu, ${\displaystyle \rho \geq {\frac {|p|}{c^{2}}}}$ şərtinin ödənməsi deməkdir.
4. Dominant sıfır enerji vəziyyəti—Dominant enerji vəziyyətinin yalnız sıfır vektorlar üçün versiyası. İdeal maye üçün bu, dominant enerji vəziyyəti ilə yanaşı ${\displaystyle \rho ={\frac {-p}{c^{2}}}}$ olmasına da icazə verir.
5. Güclü enerji vəziyyəti—istənilən zamanşəkilli ${\displaystyle t^{\mu }}$ vektoru üçün ${\displaystyle T_{\mu \nu }\geq {\frac {1}{2}}T_{\;\sigma }^{\rho }t^{\sigma }t_{\rho }}$. İdeal maye üçün bu, ${\displaystyle \rho +{\frac {p}{c^{2}}}\geq 0}$ və ${\displaystyle \rho +3{\frac {p}{c^{2}}}\geq 0}$ şərtlərinin ödənməsi deməkdir.

İstinadlar

1. Einstein, Albert. "The Foundation of the General Theory of Relativity" (PDF). Annalen der Physik. 354 (7). 1916: 769. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702. 2012-02-06 tarixində .
2. ; ; . . San Francisco: . 1973. ISBN .

Keçidlər

2. "Arxivlənmiş surət". 2022-07-01 tarixində . İstifadə tarixi: 2022-06-30.