Viyet teoremi və ya Viyet formulası — Çevrilmiş kvadrat tənlikdə tənliyin köklərinin hasili sərbəst həddə; köklərin cəmi isə əks işarə ilə götürülmüş əmsala (b-yə) bərabərdir. Teoremə onun əsasını qoymuş "Fransua Viyetin" adı verilib. Bu formulalar əsasən cəbrdə istifadə edilir.
Düsturu
Əgər 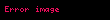
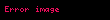

Xüsusi halda, əgər 

Əgər 

İsbatı
Viyet teoremi verilən bərabərliyi (
Bu isə doğrudur, çünki 
Həmçinin bax
İstinadlar
- , "A short account of the history of symmetric functions of roots of equations", American Mathematical Monthly, Mathematical Association of America, 37 (7), 1930: 357–365, doi:10.2307/2299273, JSTOR 2299273
- , A course in algebra, American Mathematical Society, Providence, R.I, 2003, ISBN
- Djukić, Dušan; və b., The IMO compendium: a collection of problems suggested for the International Mathematical Olympiads, 1959–2004, Springer, New York, NY, 2006, ISBN
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Viyet teoremi ve ya Viyet formulasi Cevrilmis kvadrat tenlikde tenliyin koklerinin hasili serbest hedde koklerin cemi ise eks isare ile goturulmus emsala b ye beraberdir Teoreme onun esasini qoymus Fransua Viyetin adi verilib Bu formulalar esasen cebrde istifade edilir DusturuEger x1 displaystyle x 1 ve x2 displaystyle x 2 kvadrat tenliyin ax2 bx c 0 displaystyle ax 2 bx c 0 helleridirse o zaman x1 x2 ba x1x2 ca displaystyle begin cases x 1 x 2 dfrac b a x 1 x 2 dfrac c a end cases Xususi halda eger a 1 displaystyle a 1 verilen forma x2 px q 0 displaystyle x 2 px q 0 o zaman x1 x2 p x1x2 q displaystyle begin cases x 1 x 2 p x 1 x 2 q end cases Eger x1 x2 x3 displaystyle x 1 x 2 x 3 kub tenliyinin p x ax3 bx2 cx d 0 displaystyle p x ax 3 bx 2 cx d 0 helleridirse o zaman x1 x2 x3 bax1x2 x1x3 x2x3 cax1x2x3 da displaystyle begin cases x 1 x 2 x 3 dfrac b a x 1 x 2 x 1 x 3 x 2 x 3 dfrac c a x 1 x 2 x 3 dfrac d a end cases IsbatiViyet teoremi verilen beraberliyi P x anxn an 1xn 1 a1x a0 displaystyle P x a n x n a n 1 x n 1 cdots a 1 x a 0 acmaqla isbat oluna biler aNXn an 1xn 1 a1x a0 an x x1 x x2 x xn displaystyle a N X n a n 1 x n 1 cdots a 1 x a 0 a n x x 1 x x 2 cdots x x n Bu ise dogrudur cunki x1 x2 xn displaystyle x 1 x 2 dots x n bu coxhedlinin butun helleridir Hemcinin baxFransua ViyetIstinadlar A short account of the history of symmetric functions of roots of equations American Mathematical Monthly Mathematical Association of America 37 7 1930 357 365 doi 10 2307 2299273 JSTOR 2299273 A course in algebra American Mathematical Society Providence R I 2003 ISBN 0 8218 3413 4Djukic Dusan ve b The IMO compendium a collection of problems suggested for the International Mathematical Olympiads 1959 2004 Springer New York NY 2006 ISBN 0 387 24299 6
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State



