Diferensial tənliklər

Riyaziyyatda diferensial tənlik bir və ya daha çox funksiya və onların törəmələrini əlaqələndirən bir tənlikdir. Bu cür münasibətlər olduqca yaygın olduğundan, diferensial tənliklər mühəndislik, fizika, iqtisadiyyat və biologiya da daxil olmaqla bir çox fənlərdə məşhur rol oynayır.

İstilik bərabərliyini həll etməklə yaradılan bir nasos korpusundakı istilik köçürməsinin vizuallaşdırılması . İstilik korpus içərisində yaranır və sərhəddə soyudulur, sabit bir temperatur paylanmasını təmin edir.

Diferensial tənliklərin öyrənilməsi əsasən onların həllərinin (tənliyi ödəyən edən funksiyaların məcmusu) və həllərinin xüsusiyyətlərinin öyrənilməsindən ibarətdir. Yalnız ən sadə diferensial tənliklər açıq formullarla həll edilə bilər; lakin verilmiş bir diferensial tənliyin həllərinin bir çox xüsusiyyətləri onları dəqiq hesablamadan müəyyən edilə bilər.

Həlllər üçün olmadıqda, kompüterlər istifadə edilərək sayları yaxınlaşdırıla bilər. nəzəriyyəsi, diferensial tənliklərlə təsvir olunan sistemlərin keyfiyyətcə təhlilinə diqqət yetirir, halbuki müəyyən bir dəqiqlik dərəcəsi ilə həlli təyin etmək üçün bir çox hazırlanmışdır.

Tarix

Diferensial tənliklər əvvəlcə Newton və Leibniz tərəfindən hesablama ixtirası ilə meydana gəldi. Onun 1671-ci il iş 2-ci hissəsində , Isaac Newton üç növ diferensial tənlikləri sadaladı:

${\displaystyle {\begin{aligned}&{\frac {dy}{dx}}=f(x)\\[5pt]&{\frac {dy}{dx}}=f(x,y)\\[5pt]&x_{1}{\frac {\partial y}{\partial x_{1}}}+x_{2}{\frac {\partial y}{\partial x_{2}}}=y\end{aligned}}}$

Bütün bu hallarda, y ( x ) və ya bilinməyən bir funksiyadır ${\displaystyle x_{1}}$ və ${\displaystyle x_{2}}$ ) və f verilən bir funksiyadır.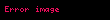

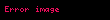
Sonsuz seriyalardan istifadə edərək bu nümunələri və digərlərini həll edir və həllərin qeyri-bərabərliyini müzakirə edir.

Jacob Bernoulli 1695-ci ildə Bernoulli diferensial tənliyini təklif etdi. Bu formanın adi bir diferensial tənliyi

${\displaystyle y'+P(x)y=Q(x)y^{n}\,}$

Növləri

Diferensial tənlikləri bir neçə növə bölmək olar. Tənzimlənmənin xüsusiyyətlərini təsvir etməkdən başqa, bu diferensial tənliklərin bu sinifləri bir həll üçün yanaşma seçimini məlumatlandırmağa kömək edə bilər. Tez-tez istifadə olunan fərqlər bu tənliyin olub-olmadığını ehtiva edir: Adi / Qismən, Xətti / Qeyri-xətti və Bircins / Qeyri-bircins. Bu siyahı tam deyil; Müxtəlif kontekstlərdə çox faydalı ola biləcək bir çox digər diferensial tənliklərin xüsusiyyətləri və alt sinifləri var.

Proqram təminatı

• : dsolve
• Xcas: desolve(y'=k*y,y)

İstinadlar

1. Newton, Isaac. (c.1671). Methodus Fluxionum et Serierum Infinitarum (The Method of Fluxions and Infinite Series), published in 1736 [Opuscula, 1744, Vol. I. p. 66].
2. "Arxivlənmiş surət". 2013-11-23 tarixində . İstifadə tarixi: 2020-05-13.
3. "Arxivlənmiş surət". 2020-01-14 tarixində . İstifadə tarixi: 2020-05-13.
4. "Arxivlənmiş surət" (PDF). 2014-07-29 tarixində (PDF). İstifadə tarixi: 2020-05-13.