| Termodinamikanın başlanğıcı |
|---|
 |
| məqalə «Termodinamika» seriyasının bir hissəsidir |
| Termodinamikanın sıfır qanunu |
| Termodinamikanın birinci qanunu |
| Termodinamikanın ikinci qanunu |
| Termodinamikanın üçüncü qanunu |
| Termodinamikanın bölmələri |
| Vəziyyət tənliyi |
| Termodinamik kəmiyyətlər |
| Termodinamik potensial |
| Termodinamik dövrə |
| Faza keçidi |
| Faza keçidləri |
| redaktə |
Termodinamika — makroskopik cisimlərin daxili durumunu tarazılıqda öyrənən elm. Başqa sözlə termodinamika qarşılıqlı çevrilmə və enerji ötürülməsini öyrənən elmdir. Fizika elminin əsas bölmələrindən biridir.
Xarakteristika

Termodinamika enerjinin və qanunların bir növdən digərinə çevrilmələrini öyrənən elm sahəsidir. İşçi maddələrin köməyi ilə istilik və mexaniki enerjilərin qarşılıqlı çevrilməsinə baxılan hissəsi texniki termodinamika adlanır. Bir-biri ilə və ətraf mühitlə qarşılıqlı əlaqəsi olan cisimləri göstərən termodinamik sistem texniki termodinamikanın əsaslarından biridir. Termodinamik sistemlərə misal olaraq silindrdə porşenin hərəkəti ilə genişlənən və ya sıxılan qazları göstərmək olar.
Termodinamik sistem olan konkret fiziki şərtləri təyin etmək üçün para-metrlərin vəziyyəti adlanan göstəricilərdən istifadə olunur. Əsas parametrlərə temperatur T, təzyiq P və həcm V (və ya xüsusi həcmin əksi olan sıxlıq ρ) daxildir. Termodinamik sistemdə işçi maddənin vəziyyətinin dəyişmə ardıcıllığı termodinamik proses adlanır. Termodinamikada vahid sahəyə düşən qüvvəyə təzyiq deyilir. Termodinamikada qüvvə vahidi olaraq Nyuton (N), sahə vahidi isə metr kvadratı (m²) qəbul olunduğundan, təzyiq N/m² ilə ölçülür.
Təzyiq 2 yerə bölünür: mütləq və izafi təzyiqlər. Mütləq təzyiqdə işçi maddənin qabın daxilindəki həqiqi təzyiqi başa düşülür. İzafi təzyiqdə mütləq təzyiqlə ətraf mühit arasındakı təzyiqlər fərqi başa düşülür. Bu fərqləri ölçən cihaz manometr adlanır.
Qapalı qabda yerləşən qazın təzyiqi atmosfer təzyiqindən kiçik olarsa, belə qazın seyrəkliyini başqa sözlə vakuumunu manometrlə deyil, vakuummetrlə ölçmək lazım gəlir. Kiçik təzyiqləri ölçmək üçün içərisinə su, civə və ya digər maye doldurulmuş mayeli cihazlardan istifadə olunur.
Termodinamik faza
Termodinamik faza, maddənin başqa hissələrindən kəskin sərhədlə ayrılan fiziki bircins hissəsinə deyilir.
Xarici şəraitdən (temperatur, təzyiq və b.) asılı olaraq maddə müxtəlif fazalarda ola bilər. Fazaların sayı aqreqat hallarının sayından çoxdur. Eyni bir aqreqat halında bir neçə faza ola bilər.
Fazalara misallar
— Bərk, maye və qaz (məsələn, buz, su və su buxarı) ;
— Tərkibi eyni olub fərqli quruluşa malik olan kristallar (məsələn, almaz və qrafit) ;
— Normal və ifratkeçirici halda olan metallar;
— Paramaqnit və ferromaqnit;
— Paraelektrik və seqnetoelektrik və s.
Faza və komponent anlayışlarını fərqləndirmək lazımdır. Komponent – sistemin elə hissəsidir ki, onun tərkibi sistemin qalan hissələrinin tərkibindən asılı olmasın. Müxtəlif qazların qarışığı (müxtəlif qazlar istənilən nisbətdə tam qarışır) birfazalı, lakin çoxkomponentli sistemdir (komponentlərin sayı sistemdə olan müxtəlif qazların sayı qədərdir). Digər tərəfdən, su və onun üzərindəki su buxarı birlikdə ikifazalı, lakin birkomponentli sistemdir (hər iki faza eyni 
Müəyyən şəraitdə maddə eyni zamanda iki və daha artıq fazada ola (yanaşı yaşaya) bilər. Məsələn, normal atmosfer təzyiqində 
Maddənin bərk və maye fazalarınn eyni zamanda yaşaya bildiyi tempertur ərimə temperaturu adlanır. Kristal cisimlərin ərimə temperaturu maddənin növündən başqa, təzyiqdən də asılıdır. Ərimə temperaturundan kiçik temperaturlarda məddə yalnız bərk, bundan böyük temperaturlada isə yalnız maye halında ola bilər.
Maye və onun üzərindəki buxar misalında fazaların tarazlığı üçün onların temperaturları (istilik tarazlığı şərti), təzyiqləri (mexaniki tarazlıq şərti) və bir fazadan digərinə və əksinə keçən molekulların sayı (maddi tarazlıq şərti) eyni olmalıdır.
Birkomponentli (eyni molekullardan ibarət) sistemin maye və ya qaz halında olması təkcə maddənin növündən və temperaturdan yox, həm də təzyiqdən asılıdır. Temperaturun hər bir qiymətinə uyğun elə bir təzyiq vardır ki, bu təzyiqdə maddə eyni zamanda həm maye, həm də qaz halında mövcud ola bilər.

Maddənin eyni zamanda həm maye, həm də qaz halında mövcud ola bildiyi hallar 
Əgər təzyiqin verilmiş 
Üçqat nöqtə
Xüsusi şəraitdə maddənin üç aqreqat halı eyni zamanda tarazlıqda ola bilər. Bunun üçün hər üç fazanın temperaturu təzyiqi və kimyəvi potensialı eyni olmalıdır. Bu, təzyiq və temperaturun yalnız bir qiymətində mümkündür. (P, T) müstəvisində həmin nöqtə üçqat nöqtə adlanır (Şəkil 2-də O nöqtəsi). Buz, su və su buxarı üçün üçqat nöqtənin koordinatları: P0 = 0,006 atm , T0 = 273K [1].

Üçqat nöqtədən kənar hallarda sistem yalnız bir fazada (bərk, maye və qaz) və ya iki fazanın tarazlığı halında olur. Cüt-cüt fazaların tarazlıq əyriləri olan AO (bərk-qaz), BO (bərk-maye) və KO (maye-qaz) əyriləri üçqat nöqtədə kəsişirlər.
Maye-qaz tarazlıq əyrisi (P, T) K nöqtəsində qurtarır. Bu nöqtəyə kritik (böhran) nöqtə deyilir. Kritik nöqtəyə uyğun kritik halda maye ilə onun buxarı arasında fərq yox olur.
Bərk-qaz və bərk-maye tarazlıq əyriləri üzərində isə kritik nöqtə müşahidə olunmur. Üçqat nöqtədən başlayan bərk-qaz tarazlıq əyrisi koordinat başlanğıcında qurtarır, bərk-maye tarazlıq əyrisi isə sonsuzluğa qədər uzanır.
Təzyiqin P< P0 qiymətlərində temperaturu artırdıqda bərk faza mayeyə çevrilmədən birbaşa qaz fazasına keçir. Bu hadisə sublimasiya, əks proses isə desublimasiya adlanır.
Maddənin bərk və maye fazalarınn eyni zamanda yaşaya bildiyi tempertur ərimə temperaturu adlanır. Kristal cisimlərin ərimə temperaturu maddənin növündən başqa, təzyiqdən də asılıdır. Verilmiş təzyiqdə ərimə temperaturundan kiçik temperaturlarda məddə yalnız bərk, bundan böyük temperaturlada isə yalnız maye halında ola bilər.
Təzyiqin P0< P< PK intervalında temperatur artarkən sistem ardıcıl olaraq hər üç fazadan keçir: bərk→maye→qaz.
Təzyiqin P> PK qiymətlərində temperaturu artırdıqda sistem OB əyrisini kəsərək bərk fazadan maye fazaya keçir, temperaturun T> T(0) qiymətlərində isə sistem OK əyrisini kəsmir-K nöqtəsindən yuxarıdan keçir (bu halda maye və qaz eyni zamanda mövcud olmur).
Faza keçidi(faza çevrilməsi)
Xarici şəraitin (temperatur, təzyiq və b.) dəyişməsi nəticəsində maddənin bir termodinamik fazadan digərinə keçməsi faza keçidi (faza çevrilməsi) adlanır[1]. Faza keçidi zamanı maddənin halını xarakterizə edən kəmiyyətlərdən biri və ya bir neçəsi sıçrayışla dəyişir.
Bütün təcrübi faktları təhlil edərək Erenfest 1933-cü ildə faza keçidlərinin təsnifatını vermişdir. Bu təsnifata görə faza keçidləri iki növə bölünür: birinci və ikinci növ faza keçidi.
Birinci növ faza keçidləri elə keçidlərə deyilir ki, keçid nöqtəsində sistemin Gibbs termodinamik potensialı (və kimyəvi potensialı) kəsilməz, lakin bu potensialın birinci törəmələri ilə təyin olunan fiziki kəmiyyətlər (entropiya və həcm) sıçrayışla dəyişsin.
elə keçidlərə deyilir ki, keçid nöqtəsində sistemin Gibbs termodinamik potensialı (kimyəvi potensial) və bu potensialın birinci törəmələri ilə təyin olunan fiziki kəmiyyətlər (entropiya və həcm) kəsilməz, lakin Gibbs potensialının ikiinci törəmələri ilə təyin olunan fiziki kəmiyyətlər (istilik tutrumu, sıxılma, istidən genişlənmə əmsalı) sıçrayışla dəyişsin.
Termodinamik potensiallar
Termodinamik potensiallar (termodinamik funksiyalar) — termodinamik sistemin tarazlıq halı haqqında bütün məlumatları özündə saxlayan funksiyalardır. Termodinamik potensiallardan hər hansı birini bilməklə sistemə aid olan bütün termodinamik parametrləri və onlar arasında ümumi münasibətləri tapmaq olur.
Qapalı sistemin termodinamik potensialları
Qapalı (zərrəciklərinin sayı dəyişməyən) sistemlərdə adətən 4 termodinamik potensial daxil edilir [1]: daxili enerji, entalpiya (istilik funksiyası), sərbəst enerji (Helmhols potensialı) və Gibbs potensialı.
Bu potensialların hamısının ölçüsü enerji vahididir. Onların mütləq qiyməti məlum olmur, yəni müəyyən sabit (bu sabit mütləq sıfırda daxili enerjinin qiymətidir) dəqiqliyi ilə tapılırlar. Lakin bu qeyri-müəyyənlik termodinamik parametlərin tapılmasına mane olmur, çünki bu parametrlər termodinamik potensialların dəyişməsi-onların birinci və ya ikinci tərtib xüsusi törəmələri kimi ifadə oluna bilir.
Termodinamik parametrlər-sistemin halını ifadə etməyə imkan verən kəmiyyətlərdir. Həcm (

Qapalı sistemin tarazlıq halında sistemə məxsus termodinamik potensialların hər biri 2 dəyişənin funksiyası kimi ifadə olunur. Bu sərbəst dəyişənlərə termodinamik potensialın təbii dəyişənləri deyilir.
Aydındır ki, termodinamik potensialların qiyməti sistemin sından asılıdır.
Sistemin termodinamik parametrlərinin və onlar arasında ümumi münasibətlərin termodinamik potensiallar daxil etməklə öyrənilməsi metodu termodinamik potensiallar metodu adlanır.
Daxili enerji
Cismlə bağlı hesablama sistemində onun bütün zərrəciklərinin hərəkəti və qarşılıqlı təsiri ilə bağlı olan bütün enerjilərin cəminə daxili enerji deyilir.






Burada 



Qeyd edək ki, sistemin özünün gördüyü iş 
Diferensial şəkildə termodinamikanın birinci qanunu:

İzoxor (

Sonuncu tənlikdən görünür ki, daxili enerjinin həcm və entropiyadan 

Mötərizənin aşağısında göstərilən kəmiyyət törəmə alınarkən sabit götürülür.



Entalpiya (İstilik funksiyası)
Entalpiya, dəyişməsi izobar (
düsturu ilə təyin edilir. Buradan
alarıq. Buradan alınır ki, termodinamik potensial olaraq entalpiyanın təbii dəyişənləri entropiya və təzyiqdir: 
Sonuncu tənlikdən görünür ki, entalpiyanın entropiya və təzyiqdən


Termodinamik potensial olaraq daxili enerji və entalpiya funksiyalarının əlverişli olmayan bir cəhəti var – onların təbii dəyişənlərindən biri təcrübədə birbaşa ölçülə bilməyən kəmiyyət olan entropiyadır. Ona görə də təbii dəyişənləri ölçülə bilən 

Sərbəst enerji (Helmhols potensialı)
Sərbəst enerji, dəyişməsi izotermik (
Sərbəst enerji
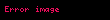
düsturu ilə təyin edilir (
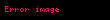
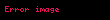
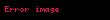
alarıq. Buradan alınır ki, termodinamik potensial olaraq sərbəst enerjinin (Helmhols potensialının) təbii dəyişənləri həcm və temperaturdur: 
Sonuncu tənlikdən görünür ki, 
Gibbsin termodinamik potensialı
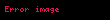
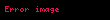
Təbii dəyişənləri 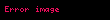
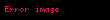
Sonuncu tənlikdən görünür ki, 
Sistemin makroskopik halını təyin edən parametrlərdən birinin dəyişməsinin digərini necə dəyişdiyini göstərən və təcrübədə ölçülə bilən kəmiyyətlərə deyilir.
İstilik tutumu (izoxor və izobar prosesdə istilik tutumu), təzyiqin izoxor termik əmsalı, izotermik sıxılma əmsalı və b. termodinamik əmsallardır.
Açıq sistemin termodinamik potensialları
Zərrəciklərinin sayı dəyişməyən sistemlərə qapalı, dəyişən sistemlərə isə açıq sistemlər deyilir.
Məsələn, qapalı qabda olan maye və onun üzərində doymuş buxar bir yerdə qapalı sistemdir, lakin bu qabdakı maye (eləcə də buxar) açıq sistemdir: temperatur və ya həcm dəyişdikdə maye və buxar fazalarda olan molekulların sayı dəyişir.
Başqa misallar:
— bir-biri ilə kontaktda olan bərk və maye fazaların hər biri açıq sistemdir (sistemə istilik verdikdə fazalardakı molekulların sayı dəyişir);
— qapalı qabda qabın divarları ilə tarazlıqda olan foton qazı (divarın temperaturu dəyişdikdə fotonların sayı dəyişir);
— kristallarda fonon qazı (kristalın temperaturu dəyişdikdə fononların sayı dəyişir);
— yarımkeçiricilərdə keçirici zonada olan elektronlar, eləcə də valent zonada olan deşiklər (temperatur dəyişdikdə onların sayı dəyişir);
— kimyəvi reaksiyalar zamanı komponentlər (reaksiya prosesində hər bir komponentin zərrəciklərinin sayı dəyişir) və s.
Açıq sistemlərin termodinamik halı yuxarıda qeyd etdiyimiz dörd parametrdən (həcm — V, entropiya — S, təzyiq — P və temperatur — T) başqa, sistemdə olan zərrəciklərin sayı ilə təyin olunur. Ona görə də tarazlıq halında açıq sistemə məxsus termodinamik potensialların hər biri iki deyil, üç dəyişənin funksiyası kimi ifadə olunur: üçüncü dəyişən zərrəciklərin sayıdır.
Qeyd edək ki, yuxarıda tanış olduğumuz dörd termodinamik potensialın hamısı additiv kəmiyyətdir — onların qiyməti zərrəciklərin sayı ilə düz mütənasibdir [1,2]. Zərrəciklərinin sayı dəyişən sistemlərin halını təsvir etmək üçün kimyəvi potensial (μ) anlayışından istifadə edilir.
– iş görmədən sistemə bir zərrəcik əlavə edəndə sistemin enerjisinin dəyişməsinə bərabər olan kəmiyyətdir.
Sistemdəki zərrəciklərin sayı N qədər dəyişəndə onun enerjisinin dəyişməsi μN — ə bərabər olar, deməli, termodinamik potensialların yuxarıda verilmiş ifadələrinin hər birinə μN həddi əlavə olunmalıdır. Beləliklə, termodinamik potensialların diferensialları üçün yaza bilərik:
Bu ifadələrdən görünür ki, kimyəvi potensialı termodinamik funksiyaların hər birini 

Qeyd edək ki, müxtəlif hallarda kimyəvi potensial müxtəlif parametrlərin funksiyası olacaq. Məsələn, termodinamik potensial olaraq Gibbsin 

Böyük termodinamik potensial
Açıq sistemlərdə daha bir termodinamik potensial daxil edilir. 
Diferensialı
ifadəsi ilə təyin olunan
funksiyasına böyük termodinamik potensial və ya omeqa-potensial deyilir. Bu funksiyanın təbii dəyişənləri 


Sistemə mexaniki təzyiq qüvvəsindən fərqli xarici qüvvələr təsir etdikdə, bu təsirlərə məxsus enerjiləri (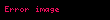



Termodinamik əmsallar
Termodinamik əmsallar, sistemin makroskopik halını təyin edən parametrlərdən birinin dəyişməsinin digər parametrləri necə dəyişdiyini göstərən və təcrübədə ölçülə bilən kəmiyyətlərə deyilir. İstilik tutumu (izoxor və izobar prosesdə istilik tutumu), təzyiqin izoxor termik əmsalı, izotermik sıxılma əmsalı və b. termodinamik əmsallardır.
İstilik tutumu
Ədədi qiymətcə, sistemin (maddənin) temperaturunu bir dərəcə dəyişmək üçün lazım olan istilik miqdarına bərabər olan kəmiyyətə istilik tutumu deyilir [1].
Xüsusi istilik tutumu və molyar istilik tutumu anlayışlarından da istifadə edilir.
Bir kq (bir mol) maddənin temperaturunu bir dərəcə dəyişmək üçün lazım olan istilik miqdarına bərabər olan kəmiyyətə xüsusi (molyar) istilik tutumu deyilir.
İstilik tutumunu iki şəraitdə — izoxor (

İzoxor istililik tutumu : 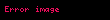
İzobar istililik tutumu: 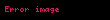
Burada 
Həcmin istidən genişlənmə əmsalı
Ədədi qiymətcə, sistemin temperaturunu bir dərəcə dəyişdikdə onun vahid həcminin dəyişməsinə bərabər olan kəmiyyətə həcmin istidən genişlənmə əmsalı deyilir.
Bu əmsalı iki şəraitdə — izobar (
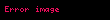
Həcmin istidən izobar genişlənmə əmsalı : 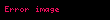
Həcmin istidən adiobat genişlənmə əmsalı : 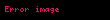
Burada 
Təzyiqin termik əmsalı
Ədədi qiymətcə, sistemin temperaturunu bir dərəcə dəyişdikdə onun təzyiqinin nisbi dəyişməsinə bərabər olan kəmiyyətə təzyiqin termik əmsalı deyilir.
Bu əmsalı iki şəraitdə — izoxor (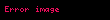
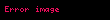
Təzyiqin izoxor termik əmsalı: 
Təzyiqin adiobat termik əmsalı: 
Sıxılma əmsalı
Ədədi qiymətcə, sistemdə təzyiqi bir vahid dəyişdikdə onun vahid həcminin dəyişməsinə bərabər olan kəmiyyətə sıxılma əmsalı deyilir.
Bu əmsalı iki şəraitdə — izotermik (
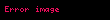
İzotermik sıxılma əmsalı: 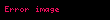
Adiobat sıxılma əmsalı: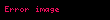
Sıxılma əmsalının tərsi həcm modulu və ya statistik modul adlanır [1] :
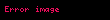
Makroskopik parametrlər kimi termodinamik əmsallar da metodu ilə hesablana bilər [1,2]. Bu əmsallar termodinamik potensialların ikinci tərtib törəmələri ilə ifadə olunur:


Burada 
İstinadlar
- Fermi, E. (1956). Thermodynamics, Dover, New York.
- Kittel, Charles & Kroemer, Herbert (1980). Thermal Physics. W. H. Freeman Company.
Ədəbiyyat
- B. M. Əsgərov. Termodinamika və statistik fizika. Bakı, 2005, 631 səh.
- Базаров. Термодинамика. Санкт-Петербург — Москва — Краснодар, 2010, 376 стр.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Termodinamikanin baslangicimeqale Termodinamika seriyasinin bir hissesidirTermodinamikanin sifir qanunuTermodinamikanin birinci qanunuTermodinamikanin ikinci qanunuTermodinamikanin ucuncu qanunuTermodinamikanin bolmeleriVeziyyet tenliyiTermodinamik kemiyyetlerTermodinamik potensialTermodinamik dovreFaza kecidiFaza kecidleriredaktePortal Fizika Termodinamika makroskopik cisimlerin daxili durumunu taraziliqda oyrenen elm Basqa sozle termodinamika qarsiliqli cevrilme ve enerji oturulmesini oyrenen elmdir Fizika elminin esas bolmelerinden biridir XarakteristikaBuxarla isleyen muherrikin misalinda numayis etdirilen tipik termodinamik proses qirmizi cox isti sari az isti mavi mediumun son temperaturu Termodinamika enerjinin ve qanunlarin bir novden digerine cevrilmelerini oyrenen elm sahesidir Isci maddelerin komeyi ile istilik ve mexaniki enerjilerin qarsiliqli cevrilmesine baxilan hissesi texniki termodinamika adlanir Bir biri ile ve etraf muhitle qarsiliqli elaqesi olan cisimleri gosteren termodinamik sistem texniki termodinamikanin esaslarindan biridir Termodinamik sistemlere misal olaraq silindrde porsenin hereketi ile genislenen ve ya sixilan qazlari gostermek olar Termodinamik sistem olan konkret fiziki sertleri teyin etmek ucun para metrlerin veziyyeti adlanan gostericilerden istifade olunur Esas parametrlere temperatur T tezyiq P ve hecm V ve ya xususi hecmin eksi olan sixliq r daxildir Termodinamik sistemde isci maddenin veziyyetinin deyisme ardicilligi termodinamik proses adlanir Termodinamikada vahid saheye dusen quvveye tezyiq deyilir Termodinamikada quvve vahidi olaraq Nyuton N sahe vahidi ise metr kvadrati m qebul olundugundan tezyiq N m ile olculur Tezyiq 2 yere bolunur mutleq ve izafi tezyiqler Mutleq tezyiqde isci maddenin qabin daxilindeki heqiqi tezyiqi basa dusulur Izafi tezyiqde mutleq tezyiqle etraf muhit arasindaki tezyiqler ferqi basa dusulur Bu ferqleri olcen cihaz manometr adlanir Qapali qabda yerlesen qazin tezyiqi atmosfer tezyiqinden kicik olarsa bele qazin seyrekliyini basqa sozle vakuumunu manometrle deyil vakuummetrle olcmek lazim gelir Kicik tezyiqleri olcmek ucun icerisine su cive ve ya diger maye doldurulmus mayeli cihazlardan istifade olunur Termodinamik fazaTermodinamik faza maddenin basqa hisselerinden keskin serhedle ayrilan fiziki bircins hissesine deyilir Xarici seraitden temperatur tezyiq ve b asili olaraq madde muxtelif fazalarda ola biler Fazalarin sayi aqreqat hallarinin sayindan coxdur Eyni bir aqreqat halinda bir nece faza ola biler Fazalara misallar Berk maye ve qaz meselen buz su ve su buxari Terkibi eyni olub ferqli qurulusa malik olan kristallar meselen almaz ve qrafit Normal ve ifratkecirici halda olan metallar Paramaqnit ve ferromaqnit Paraelektrik ve seqnetoelektrik ve s Faza ve komponent anlayislarini ferqlendirmek lazimdir Komponent sistemin ele hissesidir ki onun terkibi sistemin qalan hisselerinin terkibinden asili olmasin Muxtelif qazlarin qarisigi muxtelif qazlar istenilen nisbetde tam qarisir birfazali lakin coxkomponentli sistemdir komponentlerin sayi sistemde olan muxtelif qazlarin sayi qederdir Diger terefden su ve onun uzerindeki su buxari birlikde ikifazali lakin birkomponentli sistemdir her iki faza eyni H2O displaystyle H 2 O molekullarindan ibaretdir Mueyyen seraitde madde eyni zamanda iki ve daha artiq fazada ola yanasi yasaya biler Meselen normal atmosfer tezyiqinde t 00C displaystyle t 0 0 C T 273K displaystyle T 273K temperaturda buz ve su maye ve onun uzerindeki buxar Molekullar bir fazadan digerine kecdiyine gore bu fazalarin her biri aciq sistemdir Zerreciklerin sayi deyismeyen sistemlere termodinamikada qapali sistemler deyisen sistemlere ise aciq sistemler deyilir Mueyyen sertler odendikde bu aciq sistemler tarazliga gelir Maddenin berk ve maye fazalarinn eyni zamanda yasaya bildiyi tempertur erime temperaturu adlanir Kristal cisimlerin erime temperaturu maddenin novunden basqa tezyiqden de asilidir Erime temperaturundan kicik temperaturlarda medde yalniz berk bundan boyuk temperaturlada ise yalniz maye halinda ola biler Maye ve onun uzerindeki buxar misalinda fazalarin tarazligi ucun onlarin temperaturlari istilik tarazligi serti tezyiqleri mexaniki tarazliq serti ve bir fazadan digerine ve eksine kecen molekullarin sayi maddi tarazliq serti eyni olmalidir Birkomponentli eyni molekullardan ibaret sistemin maye ve ya qaz halinda olmasi tekce maddenin novunden ve temperaturdan yox hem de tezyiqden asilidir Temperaturun her bir qiymetine uygun ele bir tezyiq vardir ki bu tezyiqde madde eyni zamanda hem maye hem de qaz halinda movcud ola biler 1 Fazalarin tarazliq eyrisi Maddenin eyni zamanda hem maye hem de qaz halinda movcud ola bildiyi hallar P T displaystyle P T mustevisinde bir eyri ile ifade olunur Sekil 1 de AB eyrisi Bu eyri fazalarin tarazliq eyrisi adlanir Tarazliq eyrisi P T displaystyle P T mustevisini iki hisseye bolur Eyrinin sol terefindeki hallarda yalniz maye faza sag terefindeki hallarda ise yalniz qaz fazasi mumkundur Tarazliq eyrisi uzerindeki hallarda her iki faza yanasi yasayir yeni maye ve qaz fazalari tarazliqdadir Eyri boyunca hereket etdikde tarazliq pozulmur lakin maddenin muxtelif fazalarinin nisbi miqdari deyisir Eger tezyiqin verilmis P0 displaystyle P 0 qiymetinde temperaturu artirmaqla xaricden istilik vermekle sistemin halini deyisdirsek sistem a1 displaystyle a 1 halindan tarazliq eyrisi ile kesisene qeder bircins olaraq maye halinda qalir eyri uzerindeki a0 displaystyle a 0 noqtesine uygun olan halda sistem tebeqelesir yeni faza qaz fazasi yaranir Bu noqteye uygun halda sisteme xaricden istilik verilmesine baxmayaraq sistemin temperaturu deyismir ona gore ki verilen istilik mayeni buxara cevirmeye serf olunur Mayenin hamisi buxara cevrildikden sonra buxarin temperaturu artir ve sistem a2 displaystyle a 2 halina kecir Ucqat noqte Xususi seraitde maddenin uc aqreqat hali eyni zamanda tarazliqda ola biler Bunun ucun her uc fazanin temperaturu tezyiqi ve kimyevi potensiali eyni olmalidir Bu tezyiq ve temperaturun yalniz bir qiymetinde mumkundur P T mustevisinde hemin noqte ucqat noqte adlanir Sekil 2 de O noqtesi Buz su ve su buxari ucun ucqat noqtenin koordinatlari P0 0 006 atm T0 273K 1 2 Faza diaqrami Ucqat noqteden kenar hallarda sistem yalniz bir fazada berk maye ve qaz ve ya iki fazanin tarazligi halinda olur Cut cut fazalarin tarazliq eyrileri olan AO berk qaz BO berk maye ve KO maye qaz eyrileri ucqat noqtede kesisirler Maye qaz tarazliq eyrisi P T K noqtesinde qurtarir Bu noqteye kritik bohran noqte deyilir Kritik noqteye uygun kritik halda maye ile onun buxari arasinda ferq yox olur Berk qaz ve berk maye tarazliq eyrileri uzerinde ise kritik noqte musahide olunmur Ucqat noqteden baslayan berk qaz tarazliq eyrisi koordinat baslangicinda qurtarir berk maye tarazliq eyrisi ise sonsuzluga qeder uzanir Tezyiqin P lt P0 qiymetlerinde temperaturu artirdiqda berk faza mayeye cevrilmeden birbasa qaz fazasina kecir Bu hadise sublimasiya eks proses ise desublimasiya adlanir Maddenin berk ve maye fazalarinn eyni zamanda yasaya bildiyi tempertur erime temperaturu adlanir Kristal cisimlerin erime temperaturu maddenin novunden basqa tezyiqden de asilidir Verilmis tezyiqde erime temperaturundan kicik temperaturlarda medde yalniz berk bundan boyuk temperaturlada ise yalniz maye halinda ola biler Tezyiqin P0 lt P lt PK intervalinda temperatur artarken sistem ardicil olaraq her uc fazadan kecir berk maye qaz Tezyiqin P gt PK qiymetlerinde temperaturu artirdiqda sistem OB eyrisini keserek berk fazadan maye fazaya kecir temperaturun T gt T 0 qiymetlerinde ise sistem OK eyrisini kesmir K noqtesinden yuxaridan kecir bu halda maye ve qaz eyni zamanda movcud olmur Faza kecidi faza cevrilmesi Xarici seraitin temperatur tezyiq ve b deyismesi neticesinde maddenin bir termodinamik fazadan digerine kecmesi faza kecidi faza cevrilmesi adlanir 1 Faza kecidi zamani maddenin halini xarakterize eden kemiyyetlerden biri ve ya bir necesi sicrayisla deyisir Butun tecrubi faktlari tehlil ederek Erenfest 1933 cu ilde faza kecidlerinin tesnifatini vermisdir Bu tesnifata gore faza kecidleri iki nove bolunur birinci ve ikinci nov faza kecidi Birinci nov faza kecidleri ele kecidlere deyilir ki kecid noqtesinde sistemin Gibbs termodinamik potensiali ve kimyevi potensiali kesilmez lakin bu potensialin birinci toremeleri ile teyin olunan fiziki kemiyyetler entropiya ve hecm sicrayisla deyissin ele kecidlere deyilir ki kecid noqtesinde sistemin Gibbs termodinamik potensiali kimyevi potensial ve bu potensialin birinci toremeleri ile teyin olunan fiziki kemiyyetler entropiya ve hecm kesilmez lakin Gibbs potensialinin ikiinci toremeleri ile teyin olunan fiziki kemiyyetler istilik tutrumu sixilma istiden genislenme emsali sicrayisla deyissin Termodinamik potensiallarTermodinamik potensiallar termodinamik funksiyalar termodinamik sistemin tarazliq hali haqqinda butun melumatlari ozunde saxlayan funksiyalardir Termodinamik potensiallardan her hansi birini bilmekle sisteme aid olan butun termodinamik parametrleri ve onlar arasinda umumi munasibetleri tapmaq olur Qapali sistemin termodinamik potensiallari Qapali zerreciklerinin sayi deyismeyen sistemlerde adeten 4 termodinamik potensial daxil edilir 1 daxili enerji entalpiya istilik funksiyasi serbest enerji Helmhols potensiali ve Gibbs potensiali Bu potensiallarin hamisinin olcusu enerji vahididir Onlarin mutleq qiymeti melum olmur yeni mueyyen sabit bu sabit mutleq sifirda daxili enerjinin qiymetidir deqiqliyi ile tapilirlar Lakin bu qeyri mueyyenlik termodinamik parametlerin tapilmasina mane olmur cunki bu parametrler termodinamik potensiallarin deyismesi onlarin birinci ve ya ikinci tertib xususi toremeleri kimi ifade oluna bilir Termodinamik parametrler sistemin halini ifade etmeye imkan veren kemiyyetlerdir Hecm V displaystyle V entropiya S displaystyle S tezyiq P displaystyle P ve temperatur T displaystyle T termodinamik parametrlerdir Qapali sistemin tarazliq halinda sisteme mexsus termodinamik potensiallarin her biri 2 deyisenin funksiyasi kimi ifade olunur Bu serbest deyisenlere termodinamik potensialin tebii deyisenleri deyilir Aydindir ki termodinamik potensiallarin qiymeti sistemin sindan asilidir Sistemin termodinamik parametrlerinin ve onlar arasinda umumi munasibetlerin termodinamik potensiallar daxil etmekle oyrenilmesi metodu termodinamik potensiallar metodu adlanir Daxili enerji Cismle bagli hesablama sisteminde onun butun zerreciklerinin hereketi ve qarsiliqli tesiri ile bagli olan butun enerjilerin cemine daxili enerji deyilir S displaystyle S ve V displaystyle V nin funksiyasi kimi ifade olunan daxili enerji termodinamik potensial adlanir yeni temodinamik potensial kimi daxili enerjinin tebii deyisenleri V displaystyle V ve S displaystyle S dir U U V S displaystyle U U V S Daxili enerjinin deyismesi termodinamikanin birinci qanunu ile mueyyen edilir U Q A displaystyle bigtriangleup U Q A Burada U U2 U1 displaystyle bigtriangleup U U 2 U 1 sistem 1 halindan 2 halina kecende daxili enerjisinin deyismesi Q displaystyle Q bu prosesde sistemin aldigi Q gt 0 displaystyle Q gt 0 ve ya verdiyi Q lt 0 displaystyle Q lt 0 istilik miqdari A displaystyle A sistem uzerinde xarici quvvelerin gorduyu isdir sixilmada A gt 0 displaystyle A gt 0 genislenmede A lt 0 displaystyle A lt 0 Qeyd edek ki sistemin ozunun gorduyu is A A displaystyle A A Diferensial sekilde termodinamikanin birinci qanunu dU dQ dA displaystyle dU dQ dA Izoxor V Const displaystyle V Const prosesde is gorulmediyi ucun sisteme verilen alinan istilik miqdari onun daxili enerjisinin deyismesine beraber olur dU dQ displaystyle dU dQ dA PdV displaystyle dA PdV ve termodinamikanin ikinci qanununa gore dQ TdS displaystyle dQ TdS oldugunu nezere aldiqda daxili enerjinin deyismesini diferensial formada bele yazmaq olar dU TdS PdV displaystyle dU TdS PdV Sonuncu tenlikden gorunur ki daxili enerjinin hecm ve entropiyadan U U V S displaystyle U U V S asililigini bilsek diger iki parametri temperatur ve tezyiqi daxili enerjinin xususi toremeleri kimi hesablamaq olar T U S V displaystyle T Biggr frac partial U partial S Biggl V P U V S displaystyle P Biggr frac partial U partial V Biggl S Moterizenin asagisinda gosterilen kemiyyet toreme alinarken sabit goturulur U U V S displaystyle U U V S asililigi tekce T displaystyle T ve P displaystyle P nin deyil istenilen diger termodinamik kemiyyetlerin tapilmasina imkan yaradir Meselen izoxor V Const displaystyle V Const prosesde dU dQ displaystyle dU dQ oldugu ucun sabit hecmde istilik tutumu CV Q T V displaystyle C V Biggr frac partial Q partial T Biggl V daxili enerjinin toremesi kimi asagidaki sekilde ifade olunur CV U T V displaystyle C V Biggr frac partial U partial T Biggl V Entalpiya Istilik funksiyasi Entalpiya deyismesi izobar P Const displaystyle P Const prosesde sisteme verilen ondan alinan istilik miqdarina beraber olan kemiyyetdir Entalpiya W U PV displaystyle W U PV dusturu ile teyin edilir Buradan dW dU PdV VdP displaystyle dW dU PdV VdP Bu ifadede dU TdS PdV displaystyle dU TdS PdV oldugunu nezere alsaq entalpiyanin deyismesi ucun dW TdS VdP displaystyle dW TdS VdP alariq Buradan alinir ki termodinamik potensial olaraq entalpiyanin tebii deyisenleri entropiya ve tezyiqdir W W S P displaystyle W W S P Sonuncu tenlikden gorunur ki entalpiyanin entropiya ve tezyiqdenW W S P displaystyle W W S P asililigini bilsek diger iki parametri temperatur ve hecmi onun xususi toremeleri kimi tapmaq olar T W S P displaystyle T Biggr frac partial W partial S Biggl P V W P S displaystyle V Biggr frac partial W partial P Biggl S W W S P displaystyle W W S P asililigi melum olduqda istenilen termodinamik kemiyyeti tapmaq olar Meselen izobar P Const displaystyle P Const prosesde dW dQ displaystyle dW dQ oldugu ucun sabit tezyiqde istilik tutumu CP W P P displaystyle C P Biggr frac partial W partial P Biggl P Termodinamik potensial olaraq daxili enerji ve entalpiya funksiyalarinin elverisli olmayan bir ceheti var onlarin tebii deyisenlerinden biri tecrubede birbasa olcule bilmeyen kemiyyet olan entropiyadir Ona gore de tebii deyisenleri olcule bilen P displaystyle P T displaystyle T V displaystyle V parametrleri olan termodinamik potensiallar daxil edilir Serbest enerji Helmhols potensiali Serbest enerji deyismesi izotermik T Const displaystyle T Const prosesde gorulen ise beraber ola kemiyyetdir Basqa sozle serbest enerji daxili enerjinin ise cevrile bilen hissesidir Serbest enerji F U TS displaystyle F U TS dusturu ile teyin edilir TS displaystyle TS e bezen bagli enerji deyilir Buradan dF dU TdS SdT displaystyle dF dU TdS SdT Bu ifadede dU TdS PdV displaystyle dU TdS PdV oldugunu nezere alsaq serbest enerjinin deyismesi ucun dF PdV SdT displaystyle dF PdV SdT alariq Buradan alinir ki termodinamik potensial olaraq serbest enerjinin Helmhols potensialinin tebii deyisenleri hecm ve temperaturdur F F V T displaystyle F F V T Sonuncu tenlikden gorunur ki F F V T displaystyle F F V T asililigini bilsek diger iki parametri tezyiq ve entropiyani onun xususi toremeleri kimi tapmaq olar P F V T displaystyle P Biggr frac partial F partial V Biggl T S F T V displaystyle S Biggr frac partial F partial T Biggl V F F V T displaystyle F F V T asililigi melum olduqda istenilen termodinamik kemiyyeti tapmaq olar Gibbsin termodinamik potensiali G F PV displaystyle G F PV isare edek bu ifadeni bele de yazmaq olar G F PV W TS U TS PV displaystyle G F PV W TS U TS PV Onda dG dF PdV VdP displaystyle dG dF PdV VdP Bu ifadede yuxarida alinmis dF PdV SdT displaystyle dF PdV SdT munasibetini nezere alsaq dG SdT VdP displaystyle dG SdT VdP Tebii deyisenleri T displaystyle T ve P displaystyle P olan G G T P displaystyle G G T P funksiyasi Gibbsin termodinamik potensiali adlanir Termodinamik tedqiqatlarda Gibbs potensialindan daha cox istifade edilir Bu onunla baglidir ki murekkeb sistemin tarazliq halinda Gibbs potensialinin tebii deyisenleri olan T ve P sistemin her yerinde eyni olur Sonuncu tenlikden gorunur ki G G T P displaystyle G G T P funksiyasinin aciq seklinii bilsek hecmi ve entropiyani tapa bilerik V G P T displaystyle V Biggr frac partial G partial P Biggl T S G T P displaystyle S Biggr frac partial G partial T Biggl P G G T P displaystyle G G T P asililigi melum olduqda istenilen termodinamik kemiyyeti ve termodinamik emsallari tapmaq olar Sistemin makroskopik halini teyin eden parametrlerden birinin deyismesinin digerini nece deyisdiyini gosteren ve tecrubede olcule bilen kemiyyetlere deyilir Istilik tutumu izoxor ve izobar prosesde istilik tutumu tezyiqin izoxor termik emsali izotermik sixilma emsali ve b termodinamik emsallardir Aciq sistemin termodinamik potensiallari Zerreciklerinin sayi deyismeyen sistemlere qapali deyisen sistemlere ise aciq sistemler deyilir Meselen qapali qabda olan maye ve onun uzerinde doymus buxar bir yerde qapali sistemdir lakin bu qabdaki maye elece de buxar aciq sistemdir temperatur ve ya hecm deyisdikde maye ve buxar fazalarda olan molekullarin sayi deyisir Basqa misallar bir biri ile kontaktda olan berk ve maye fazalarin her biri aciq sistemdir sisteme istilik verdikde fazalardaki molekullarin sayi deyisir qapali qabda qabin divarlari ile tarazliqda olan foton qazi divarin temperaturu deyisdikde fotonlarin sayi deyisir kristallarda fonon qazi kristalin temperaturu deyisdikde fononlarin sayi deyisir yarimkeciricilerde kecirici zonada olan elektronlar elece de valent zonada olan desikler temperatur deyisdikde onlarin sayi deyisir kimyevi reaksiyalar zamani komponentler reaksiya prosesinde her bir komponentin zerreciklerinin sayi deyisir ve s Aciq sistemlerin termodinamik hali yuxarida qeyd etdiyimiz dord parametrden hecm V entropiya S tezyiq P ve temperatur T basqa sistemde olan zerreciklerin sayi ile teyin olunur Ona gore de tarazliq halinda aciq sisteme mexsus termodinamik potensiallarin her biri iki deyil uc deyisenin funksiyasi kimi ifade olunur ucuncu deyisen zerreciklerin sayidir Qeyd edek ki yuxarida tanis oldugumuz dord termodinamik potensialin hamisi additiv kemiyyetdir onlarin qiymeti zerreciklerin sayi ile duz mutenasibdir 1 2 Zerreciklerinin sayi deyisen sistemlerin halini tesvir etmek ucun kimyevi potensial m anlayisindan istifade edilir is gormeden sisteme bir zerrecik elave edende sistemin enerjisinin deyismesine beraber olan kemiyyetdir Sistemdeki zerreciklerin sayi N qeder deyisende onun enerjisinin deyismesi mN e beraber olar demeli termodinamik potensiallarin yuxarida verilmis ifadelerinin her birine mN heddi elave olunmalidir Belelikle termodinamik potensiallarin diferensiallari ucun yaza bilerik dU TdS PdV mdN displaystyle dU TdS PdV mu dN dW TdS VdP mdN displaystyle dW TdS VdP mu dN dF PdV SdT mdN displaystyle dF PdV SdT mu dN dG SdT VdP mdN displaystyle dG SdT VdP mu dN Bu ifadelerden gorunur ki kimyevi potensiali termodinamik funksiyalarin her birini N displaystyle N e gore diferensiallamaqla tapmaq olar m U N S V W N S P F N T V G N P T displaystyle mu Biggr frac partial U partial N Biggl S V Biggr frac partial W partial N Biggl S P Biggr frac partial F partial N Biggl T V Biggr frac partial G partial N Biggl P T Qeyd edek ki muxtelif hallarda kimyevi potensial muxtelif parametrlerin funksiyasi olacaq Meselen termodinamik potensial olaraq Gibbsin G displaystyle G termodinamik potensialini gotursek m displaystyle mu yalniz temperatur T displaystyle T ve tezyiqin P displaystyle P funksiyasidir ve zerreciklerin sayindan N displaystyle N asili deyil Boyuk termodinamik potensial Aciq sistemlerde daha bir termodinamik potensial daxil edilir dF PdV SdT mdN displaystyle dF PdV SdT mu dN beraberliyinde d mN mdN Ndm displaystyle d mu N mu dN Nd mu oldugunu nezere alsaq d F mN PdV SdT Ndm displaystyle d F mu N PdV SdT Nd mu Diferensiali dW PdV SdT Ndm displaystyle d Omega PdV SdT Nd mu ifadesi ile teyin olunan W F mN U TS mN displaystyle Omega F mu N U TS mu N funksiyasina boyuk termodinamik potensial ve ya omeqa potensial deyilir Bu funksiyanin tebii deyisenleri T displaystyle T V displaystyle V ve m displaystyle mu dur W W T V m displaystyle Omega Omega Bigl T V mu Bigr Bu funksiyanin aciq seklini bilsek zerreciklerin sayini tezyiqi entropiyani ve s tapa bilerik N W m T V displaystyle N Biggr frac partial Omega partial mu Biggl T V P W V T m displaystyle P Biggr frac partial Omega partial V Biggl T mu S W T V m displaystyle S Biggr frac partial Omega partial T Biggl V mu Sisteme mexaniki tezyiq quvvesinden ferqli xarici quvveler tesir etdikde bu tesirlere mexsus enerjileri Wf displaystyle W f de boyuk termodinamik potensiala elave etmek lazimdir Eger aciq sistem xarici elektrik sahesinde olarsa Wf P E displaystyle W f Bigl vec P vec E Bigr maqnit sahesinde olarsa Wf M H displaystyle W f Bigl vec M vec H Bigr Bu ifadelerde E displaystyle vec E xarici elektrik sahesinin intensivliyi P displaystyle vec P bu elektrik sahesinin tesiri ile muhitde yaranmis polyarizasiya vektoru H displaystyle vec H xarici maqnit sahesinin intensivliyi M displaystyle vec M maqnit sahesinin tesiri ile muhitde yaranan maqnitlesme vektorudur Termodinamik emsallarTermodinamik emsallar sistemin makroskopik halini teyin eden parametrlerden birinin deyismesinin diger parametrleri nece deyisdiyini gosteren ve tecrubede olcule bilen kemiyyetlere deyilir Istilik tutumu izoxor ve izobar prosesde istilik tutumu tezyiqin izoxor termik emsali izotermik sixilma emsali ve b termodinamik emsallardir Istilik tutumu Ededi qiymetce sistemin maddenin temperaturunu bir derece deyismek ucun lazim olan istilik miqdarina beraber olan kemiyyete istilik tutumu deyilir 1 Xususi istilik tutumu ve molyar istilik tutumu anlayislarindan da istifade edilir Bir kq bir mol maddenin temperaturunu bir derece deyismek ucun lazim olan istilik miqdarina beraber olan kemiyyete xususi molyar istilik tutumu deyilir Istilik tutumunu iki seraitde izoxor V Const displaystyle V Const ve izobar P Const displaystyle P Const seraitde olcurler Izoxor istililik tutumu CV Q T V displaystyle C V Bigl frac partial Q partial T Bigr V Izobar istililik tutumu CP Q T P displaystyle C P Bigl frac partial Q partial T Bigr P Burada Q displaystyle Q istilik miqdari T displaystyle T temperaturdur Hecmin istiden genislenme emsali Ededi qiymetce sistemin temperaturunu bir derece deyisdikde onun vahid hecminin deyismesine beraber olan kemiyyete hecmin istiden genislenme emsali deyilir Bu emsali iki seraitde izobar P Const displaystyle P Const ve adiobat S Const displaystyle S Const seraitde olcurler Hecmin istiden izobar genislenme emsali aP 1V V T P displaystyle alpha P frac 1 V Bigl frac partial V partial T Bigr P Hecmin istiden adiobat genislenme emsali aS 1V V T S displaystyle alpha S frac 1 V Bigl frac partial V partial T Bigr S Burada S displaystyle S entropiyadir Tezyiqin termik emsali Ededi qiymetce sistemin temperaturunu bir derece deyisdikde onun tezyiqinin nisbi deyismesine beraber olan kemiyyete tezyiqin termik emsali deyilir Bu emsali iki seraitde izoxor V Const displaystyle V Const ve adiobat S Const displaystyle S Const seraitde olcurler Tezyiqin izoxor termik emsali bV 1P P T V displaystyle beta V frac 1 P Bigl frac partial P partial T Bigr V Tezyiqin adiobat termik emsali bS 1P P T S displaystyle beta S frac 1 P Bigl frac partial P partial T Bigr S Sixilma emsali Ededi qiymetce sistemde tezyiqi bir vahid deyisdikde onun vahid hecminin deyismesine beraber olan kemiyyete sixilma emsali deyilir Bu emsali iki seraitde izotermik T Const displaystyle T Const ve adiobat S Const displaystyle S Const seraitde olcurler Izotermik sixilma emsali gT 1V V P T displaystyle gamma T frac 1 V Bigl frac partial V partial P Bigr T Adiobat sixilma emsali gS 1V V P S displaystyle gamma S frac 1 V Bigl frac partial V partial P Bigr S Sixilma emsalinin tersi hecm modulu ve ya statistik modul adlanir 1 BT gT 1 V P V T displaystyle B T gamma T 1 V Bigl frac partial P partial V Bigr T BS gS 1 V P V S displaystyle B S gamma S 1 V Bigl frac partial P partial V Bigr S Makroskopik parametrler kimi termodinamik emsallar da metodu ile hesablana biler 1 2 Bu emsallar termodinamik potensiallarin ikinci tertib toremeleri ile ifade olunur CV T 2F T2 V displaystyle C V T Bigl frac partial 2 F partial T 2 Bigr V CP T 2F T2 P displaystyle C P T Bigl frac partial 2 F partial T 2 Bigr P aP 1V 2F T P displaystyle alpha P frac 1 V Bigl frac partial 2 Phi partial T partial P Bigr bV 1P 2F T V displaystyle beta V frac 1 P Bigl frac partial 2 F partial T partial V Bigr gT 1V 2F P2 T displaystyle gamma T frac 1 V Bigl frac partial 2 Phi partial P 2 Bigr T Burada F displaystyle F serbest enerji F displaystyle Phi ise Gibbsin termodinamik potensialidir IstinadlarFermi E 1956 Thermodynamics Dover New York Kittel Charles amp Kroemer Herbert 1980 Thermal Physics W H Freeman Company EdebiyyatB M Esgerov Termodinamika ve statistik fizika Baki 2005 631 seh Bazarov Termodinamika Sankt Peterburg Moskva Krasnodar 2010 376 str
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans