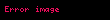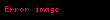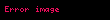Neş tarazlığı (ing. Nash equilibrium) oyunlar nəzəriyyəsində — iki və ya daha çox oyunçuların iştirak etdikləri üçün həll konseptidir. Con Neş belə bir tarazlığın mövcud olduğunu hər hansı bir sonlu oyunda qarışıq strategiyalarda sübut etdi.
Bu konseptdə aşağıdakılar fərz olunur:
- hər bir oyunçu digər hər bir oyunçunun tarazlıq strategiyasını bilir,
- və heç bir oyunçu yalnız öz strategiyasını dəyişməklə öz qazancını artıra bilməz.
Əgər bütün oyunçular öz strategiyalarını seçmişlərsə və heç bir oyunçu yalnız öz strategiyasını dəyişməklə artıq heç bir qazanc əldə edə bilmirsə, onda bu strategiyalar seçimi və müvafiq qazanclar (mükafatlar) Neş tarazlığın təşkil edir.
Tarixi

Bu konsepsiya ilk dəfə Antuan Oqüst Kurno tərəfindən istifadə edilmişdir. Kurno oyununda Neş tarazlığı dediyimizi necə tapacağımızı göstərdi. Neş, bu cür tarazlığın istənilən sayda oyunçu ilə sonlu oyunlar üçün mövcud olduğunu sübut edən ilk şəxs idi. Bu, kooperativ olmayan oyunlar haqqında 1950-ci ildə yazdığı dissertasiyasında edilmişdir.
Neşdən əvvəl bu, yalnız Con fon Neyman və Oskar Morqenştern tərəfindən 2 əlli oyunlar üçün sübut edilmişdir.
Riyazi tərtibi
Fərz edək ki, 
normal formadakı şəxslərlə , burada S — saf strategiyaların məcmusu və H
— qələbə toplusu. Hər bir oyunçu


qazanır. Nəticənin bütün strategiya profilindən asılı olduğunu unutmayın: yalnız
strategiyasına deyil , oyunçunun özü tərəfindən i tərəfindən seçilmiş, eyni zamanda başqalarının
strategiyalarından seçilmiş, yəni
üçün
bütün strategiyalarıdır. Strategiya profili
, strategiyanızı
-dan
-ə dəyişdirməyin heç bir oyunçu üçün faydalı olmadığı bir Nash tarazlığıdır.
, yəni hər hansı bir
üçün
Oyun təmiz strategiyalarda və ya qarışıq strategiyalarda bir Nash tarazlığına sahib ola bilər (yəni stokastik olaraq sabit bir tezliklə təmiz bir strategiya seçərkən). Neş sübut etdi ki, qarışıq strategiyalara icazə verilsə, n oyunçuların hər oyununda ən azı bir Neş tarazlığı olacaqdır.
Konsepsiyadan istifadə nümunələri
Sosiologiya
Rasional seçim sosioloji nəzəriyyədə cəmiyyətin sabit vəziyyətinin (sosial tarazlıq) optimal vəziyyətindən (sosial optimum) fərqli ola biləcəyi ayrıca vurğulanır. Belə suboptimal, lakin sabit vəziyyətlər sosiologiyada Neş tarazlığı adlanır.
| Aktyor B | |||
|---|---|---|---|
| 1 | 2 | ||
| Aktyor A | 1 | A: +1, B: +1 | A: −1, B: +2 |
| 2 | A: +2, B: −1 | A: 0, B: 0 | |
Soldakı cədvəl, iki aktyor (aktyor) üçün tərtib edilmiş oyun nəzəriyyəsi baxımından hərəkətin quruluşunu göstərir. Hər bir aktyorun 1 və 2 nömrələri ilə təyin olunmuş iki hərəkət variantı var, hərəkət üçün müəyyən variantları seçərkən alacaqları mükafat əmsalları cədvəlin müvafiq xanalarında göstərilir. Fərz edək ki, hazırda hər iki aktyor 2-ci əməliyyatı istifadə edir və mükafatları müvafiq olaraq sıfıra bərabərdir. Əməliyyat 1 seçərək A aktyoru bir vəziyyətlə vəziyyətini pisləşdirəcək (A: −1, B: +2). Eynilə, aktyor B müstəqil olaraq seçim 1-i seçir, A aktyor isə hərəkət 2-dən istifadə etməyə davam edərkən vəziyyətini daha da pisləşdirəcəkdir (A: +2, B: −1). Beləliklə, hər iki aktyorun hər ikisinin 1 hərəkətindən (mükafat - A: +1, B: +1) istifadə etdikləri bir vəziyyətdə olmalarının optimal olacağını başa düşməsinə baxmayaraq, ikisinin də vəziyyəti dəyişdirmək üçün bir motivi yoxdur. və tarazlıq bu cür motivlərin olmamasının nəticəsidir. Sistem onsuz da optimal vəziyyətdədirsə (hər iki aktyor 1-ci hərəkəti seçdikdə), hər ikisi daima hərəkət 2-ni istifadə etməyə cazibədar olacaq və bu da onları digər oyunçu hesabına mükafatlandıracaq. Bu nümunə iki sosial dövlətin mövcudluğunu göstərir: sabit, lakin qeyri-optimaldır (hər iki aktyor variant 2-dən istifadə edir); eyni zamanda ikinci optimal, lakin qeyri-sabitdir (hər iki aktyor seçim 1-dən istifadə edir)
Siyasi Elm
Siyasi nəzəriyyədəki müxtəlif fenomenləri izah etmək üçün Nash tarazlığının daha zəif bir versiyası olan nüvə konsepsiyasından tez-tez istifadə olunur. Nüvə, hər birində yeni (bu nüvədə olmayan) bir dövlət qurmağı bacaran heç bir aktyor qrupunun vəziyyətini bu nüvədəki vəziyyəti ilə müqayisədə yaxşılaşdırmayacağı bir sıra dövlətlərdir.
İqtisadiyyat
Sektorda # 1 və # 2 adlı iki firma var. Firmaların hər biri iki qiymət səviyyəsini təyin edə bilər: “yüksək” və “aşağı”. Hər iki firma yüksək qiymət seçərsə, hər birinin 3 milyon qazancı olacaq, hər ikisi aşağı seçərsə, hər biri 2 milyon qazanacaq, ancaq biri yüksək, digəri aşağı seçərsə, ikincisi 4 milyon, birincisi isə yalnız 1 milyon qazanacaqdır. Cəmi ən sərfəli seçim, eyni zamanda yüksək qiymətlərin seçilməsidir (məbləğ = 6 milyon). Bununla birlikdə, bu vəziyyət (kartel razılaşması olmadığı təqdirdə) bu strategiyadan çıxmış bir firma üçün açılan nisbi qazanc ehtimalı səbəbindən qeyri-sabitdir. Buna görə hər iki şirkətin aşağı qiymətləri seçmə ehtimalı daha yüksəkdir. Bu seçim maksimum ümumi qazanc verməməsinə baxmayaraq (məbləğ = 4 milyon), rəqibin qarşılıqlı optimal strategiyadan kənara çıxaraq əldə edə biləcəyi nisbi qazancını istisna edir. Bu vəziyyətə "Nash tarazlığı" deyilir .
Müharibə
Qarşılıqlı təmin edilmiş məhv konsepsiyası. Nüvə silahı olan heç bir tərəf ya cəzasız olaraq bir qarşıdurmaya başlaya bilər, nə də birtərəfli qaydada tərksilah edilə bilər.
İstinadlar
- De Fraja, G.; Oliveira, T.; Zanchi, L. "Must Try Harder: Evaluating the Role of Effort in Educational Attainment". Review of Economics and Statistics. 92 (3). 2010: 577. doi:10.1162/REST_a_00013.
- Schelling, Thomas, The Strategy of Conflict 2020-08-06 at the Wayback Machine, copyright 1960, 1980, Harvard University Press, ISBN .
- Osborne, Martin J.; . A Course in Game Theory. Cambridge, MA: MIT. 12 Jul 1994. səh. 14. ISBN .
- Thorpe, Robert B.; Jennings, Simon; Dolder, Paul J. "Risks and benefits of catching pretty good yield in multispecies mixed fisheries". ICES Journal of Marine Science. 74 (8). 2017: 2097–2106. doi:10.1093/icesjms/fsx062.,
- "Marketing Lessons from Dr. Nash - Andrew Frank". 2015-05-25. 2015-09-06 tarixində . İstifadə tarixi: 2015-08-30.
- Djehiche, B.; Tcheukam, A.; Tembine, H. "A Mean-Field Game of Evacuation in Multilevel Building". IEEE Transactions on Automatic Control. 62 (10). 2017: 5154–5169. doi:10.1109/TAC.2017.2679487. ISSN 0018-9286.
- J. Von Neumann, O. Morgenstern, Theory of Games and Economic Behavior, copyright 1944, 1953, Princeton University Press
- Carmona, Guilherme; Podczeck, Konrad. "On the Existence of Pure Strategy Nash Equilibria in Large Games" (PDF). . 144 (3). 2009: 1300–1319. doi:10.1016/j.jet.2008.11.009. SSRN 882466.[ölü keçid]
- Джеймс С. Коулман. Экономическая социология с точки зрения теории рационального выбора (PDF). 5 (Экономическая социология). 2004. 35–44.
Ədəbiyyat
Oyun nəzəriyyəsi dərslikləri
- Dixit, Avinash, Susan Skeath and David Reiley. Games of Strategy. W.W. Norton & Company. (Third edition in 2009)
- Dutta, Prajit K., Strategies and games: theory and practice, MIT Press, 1999, ISBN . Suitable for undergraduate and business students.
- Fudenberg, Drew and Jean Tirole (1991) Game Theory MIT Press.
- Leyton-Brown, Kevin; Shoham, Yoav, Essentials of Game Theory: A Concise, Multidisciplinary Introduction, San Rafael, CA: Morgan & Claypool Publishers, 2008, ISBN , 2019-04-10 tarixində , İstifadə tarixi: 2020-11-06. An 88-page mathematical introduction; see Chapter 2. Free online 2000-08-15 at the Wayback Machine at many universities.
- Oskar Morgenstern and John von Neumann (1947) The Theory of Games and Economic Behavior Princeton University Press
- , Game theory: analysis of conflict, Harvard University Press, 1997, ISBN
- , Game Theory for Business: A Primer in Strategic Gaming, , 2010, ISBN
- ; Osborne, Martin J., A course in game theory, MIT Press, 1994, ISBN . A modern introduction at the graduate level.
- Shoham, Yoav; Leyton-Brown, Kevin, , New York: Cambridge University Press, 2009, ISBN , 2011-05-01 tarixində orijinalından arxivləşdirilib, İstifadə tarixi: 2020-11-06. A comprehensive reference from a computational perspective; see Chapter 3. Downloadable free online 2011-06-15 at the Wayback Machine.
- Gibbons, Robert, Game Theory for Applied Economists, Princeton University Press (July 13, 1992), 1992, ISBN . Lucid and detailed introduction to game theory in an explicitly economic context.
- Osborne, Martin, An introduction to game theory, Oxford University Press, 2004, ISBN . Introduction to Nash equilibrium.
- Binmore, Ken, Playing for Real: A Text on Game Theory, Oxford University Press, 2007, ISBN .
Orijinal Neş sənədləri
- John Forbes Nash (1950) "Equilibrium points in n-person games" Proceedings of the National Academy of Sciences 36(1):48-49.
- John Forbes Nash (1951) "Non-Cooperative Games" The Annals of Mathematics 54(2):286-295.
Digər istinadlar
- Mehlmann, A. (2000) The Game's Afoot! Game Theory in Myth and Paradox, American Mathematical Society.
- Sylvia Nasar (1998), A Beautiful Mind, Simon & Schuster.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Nes tarazligi ing Nash equilibrium oyunlar nezeriyyesinde iki ve ya daha cox oyuncularin istirak etdikleri ucun hell konseptidir Con Nes bele bir tarazligin movcud oldugunu her hansi bir sonlu oyunda qarisiq strategiyalarda subut etdi Bu konseptde asagidakilar ferz olunur her bir oyuncu diger her bir oyuncunun tarazliq strategiyasini bilir ve hec bir oyuncu yalniz oz strategiyasini deyismekle oz qazancini artira bilmez Eger butun oyuncular oz strategiyalarini secmislerse ve hec bir oyuncu yalniz oz strategiyasini deyismekle artiq hec bir qazanc elde ede bilmirse onda bu strategiyalar secimi ve muvafiq qazanclar mukafatlar Nes tarazligin teskil edir TarixiBu konsepsiya ilk defe Antuan Oqust Kurno terefinden istifade edilmisdir Kurno oyununda Nes tarazligi dediyimizi nece tapacagimizi gosterdi Nes bu cur tarazligin istenilen sayda oyuncu ile sonlu oyunlar ucun movcud oldugunu subut eden ilk sexs idi Bu kooperativ olmayan oyunlar haqqinda 1950 ci ilde yazdigi dissertasiyasinda edilmisdir Nesden evvel bu yalniz Con fon Neyman ve Oskar Morqenstern terefinden 2 elli oyunlar ucun subut edilmisdir Riyazi tertibiFerz edek ki S H displaystyle S H n normal formadaki sexslerle burada S saf strategiyalarin mecmusu ve H qelebe toplusu Her bir oyuncui 1 n displaystyle i in 1 n strategiya profilinde xi S displaystyle x i in S strategiyasini secende x x1 xn displaystyle x x 1 x n oyuncu i Hi x displaystyle H i x qazanir Neticenin butun strategiya profilinden asili oldugunu unutmayin yalniz xi displaystyle x i strategiyasina deyil oyuncunun ozu terefinden i terefinden secilmis eyni zamanda basqalarinin x i displaystyle x i strategiyalarindan secilmis yeni j i displaystyle j neq i ucun xj displaystyle x j butun strategiyalaridir Strategiya profili x S displaystyle x in S strategiyanizi xi displaystyle x i danxi displaystyle x i e deyisdirmeyin hec bir oyuncu ucun faydali olmadigi bir Nash tarazligidir i displaystyle i yeni her hansi bir i displaystyle i ucun Hi x Hi xi x i displaystyle H i x geqslant H i x i x i Oyun temiz strategiyalarda ve ya qarisiq strategiyalarda bir Nash tarazligina sahib ola biler yeni stokastik olaraq sabit bir tezlikle temiz bir strategiya secerken Nes subut etdi ki qarisiq strategiyalara icaze verilse n oyuncularin her oyununda en azi bir Nes tarazligi olacaqdir Konsepsiyadan istifade numuneleriSosiologiya Rasional secim sosioloji nezeriyyede cemiyyetin sabit veziyyetinin sosial tarazliq optimal veziyyetinden sosial optimum ferqli ola bileceyi ayrica vurgulanir Bele suboptimal lakin sabit veziyyetler sosiologiyada Nes tarazligi adlanir Aktyor B1 2Aktyor A 1 A 1 B 1 A 1 B 22 A 2 B 1 A 0 B 0 Soldaki cedvel iki aktyor aktyor ucun tertib edilmis oyun nezeriyyesi baximindan hereketin qurulusunu gosterir Her bir aktyorun 1 ve 2 nomreleri ile teyin olunmus iki hereket varianti var hereket ucun mueyyen variantlari secerken alacaqlari mukafat emsallari cedvelin muvafiq xanalarinda gosterilir Ferz edek ki hazirda her iki aktyor 2 ci emeliyyati istifade edir ve mukafatlari muvafiq olaraq sifira beraberdir Emeliyyat 1 secerek A aktyoru bir veziyyetle veziyyetini pislesdirecek A 1 B 2 Eynile aktyor B musteqil olaraq secim 1 i secir A aktyor ise hereket 2 den istifade etmeye davam ederken veziyyetini daha da pislesdirecekdir A 2 B 1 Belelikle her iki aktyorun her ikisinin 1 hereketinden mukafat A 1 B 1 istifade etdikleri bir veziyyetde olmalarinin optimal olacagini basa dusmesine baxmayaraq ikisinin de veziyyeti deyisdirmek ucun bir motivi yoxdur ve tarazliq bu cur motivlerin olmamasinin neticesidir Sistem onsuz da optimal veziyyetdedirse her iki aktyor 1 ci hereketi secdikde her ikisi daima hereket 2 ni istifade etmeye cazibedar olacaq ve bu da onlari diger oyuncu hesabina mukafatlandiracaq Bu numune iki sosial dovletin movcudlugunu gosterir sabit lakin qeyri optimaldir her iki aktyor variant 2 den istifade edir eyni zamanda ikinci optimal lakin qeyri sabitdir her iki aktyor secim 1 den istifade edir Siyasi Elm Siyasi nezeriyyedeki muxtelif fenomenleri izah etmek ucun Nash tarazliginin daha zeif bir versiyasi olan nuve konsepsiyasindan tez tez istifade olunur Nuve her birinde yeni bu nuvede olmayan bir dovlet qurmagi bacaran hec bir aktyor qrupunun veziyyetini bu nuvedeki veziyyeti ile muqayisede yaxsilasdirmayacagi bir sira dovletlerdir Iqtisadiyyat Sektorda 1 ve 2 adli iki firma var Firmalarin her biri iki qiymet seviyyesini teyin ede biler yuksek ve asagi Her iki firma yuksek qiymet secerse her birinin 3 milyon qazanci olacaq her ikisi asagi secerse her biri 2 milyon qazanacaq ancaq biri yuksek digeri asagi secerse ikincisi 4 milyon birincisi ise yalniz 1 milyon qazanacaqdir Cemi en serfeli secim eyni zamanda yuksek qiymetlerin secilmesidir mebleg 6 milyon Bununla birlikde bu veziyyet kartel razilasmasi olmadigi teqdirde bu strategiyadan cixmis bir firma ucun acilan nisbi qazanc ehtimali sebebinden qeyri sabitdir Buna gore her iki sirketin asagi qiymetleri secme ehtimali daha yuksekdir Bu secim maksimum umumi qazanc vermemesine baxmayaraq mebleg 4 milyon reqibin qarsiliqli optimal strategiyadan kenara cixaraq elde ede bileceyi nisbi qazancini istisna edir Bu veziyyete Nash tarazligi deyilir Muharibe Qarsiliqli temin edilmis mehv konsepsiyasi Nuve silahi olan hec bir teref ya cezasiz olaraq bir qarsidurmaya baslaya biler ne de birterefli qaydada terksilah edile biler IstinadlarDe Fraja G Oliveira T Zanchi L Must Try Harder Evaluating the Role of Effort in Educational Attainment Review of Economics and Statistics 92 3 2010 577 doi 10 1162 REST a 00013 Schelling Thomas The Strategy of Conflict 2020 08 06 at the Wayback Machine copyright 1960 1980 Harvard University Press ISBN 0 674 84031 3 Osborne Martin J A Course in Game Theory Cambridge MA MIT 12 Jul 1994 seh 14 ISBN 9780262150415 Thorpe Robert B Jennings Simon Dolder Paul J Risks and benefits of catching pretty good yield in multispecies mixed fisheries ICES Journal of Marine Science 74 8 2017 2097 2106 doi 10 1093 icesjms fsx062 Marketing Lessons from Dr Nash Andrew Frank 2015 05 25 2015 09 06 tarixinde Istifade tarixi 2015 08 30 Djehiche B Tcheukam A Tembine H A Mean Field Game of Evacuation in Multilevel Building IEEE Transactions on Automatic Control 62 10 2017 5154 5169 doi 10 1109 TAC 2017 2679487 ISSN 0018 9286 J Von Neumann O Morgenstern Theory of Games and Economic Behavior copyright 1944 1953 Princeton University Press Carmona Guilherme Podczeck Konrad On the Existence of Pure Strategy Nash Equilibria in Large Games PDF 144 3 2009 1300 1319 doi 10 1016 j jet 2008 11 009 SSRN 882466 olu kecid Dzhejms S Koulman Ekonomicheskaya sociologiya s tochki zreniya teorii racionalnogo vybora PDF 5 Ekonomicheskaya sociologiya 2004 35 44 EdebiyyatOyun nezeriyyesi derslikleri Dixit Avinash Susan Skeath and David Reiley Games of Strategy W W Norton amp Company Third edition in 2009 Dutta Prajit K Strategies and games theory and practice MIT Press 1999 ISBN 978 0 262 04169 0 Suitable for undergraduate and business students Fudenberg Drew and Jean Tirole 1991 Game Theory MIT Press Leyton Brown Kevin Shoham Yoav Essentials of Game Theory A Concise Multidisciplinary Introduction San Rafael CA Morgan amp Claypool Publishers 2008 ISBN 978 1 59829 593 1 2019 04 10 tarixinde Istifade tarixi 2020 11 06 An 88 page mathematical introduction see Chapter 2 Free online 2000 08 15 at the Wayback Machine at many universities Oskar Morgenstern and John von Neumann 1947 The Theory of Games and Economic Behavior Princeton University Press Game theory analysis of conflict Harvard University Press 1997 ISBN 978 0 674 34116 6 Game Theory for Business A Primer in Strategic Gaming 2010 ISBN 978 0964793873 Osborne Martin J A course in game theory MIT Press 1994 ISBN 978 0 262 65040 3 A modern introduction at the graduate level Shoham Yoav Leyton Brown Kevin New York Cambridge University Press 2009 ISBN 978 0 521 89943 7 2011 05 01 tarixinde orijinalindan arxivlesdirilib Istifade tarixi 2020 11 06 A comprehensive reference from a computational perspective see Chapter 3 Downloadable free online 2011 06 15 at the Wayback Machine Gibbons Robert Game Theory for Applied Economists Princeton University Press July 13 1992 1992 ISBN 978 0 691 00395 5 Lucid and detailed introduction to game theory in an explicitly economic context Osborne Martin An introduction to game theory Oxford University Press 2004 ISBN 978 0 19 512895 6 Introduction to Nash equilibrium Binmore Ken Playing for Real A Text on Game Theory Oxford University Press 2007 ISBN 978 0195300574 Orijinal Nes senedleri John Forbes Nash 1950 Equilibrium points in n person games Proceedings of the National Academy of Sciences 36 1 48 49 John Forbes Nash 1951 Non Cooperative Games The Annals of Mathematics 54 2 286 295 Diger istinadlar Mehlmann A 2000 The Game s Afoot Game Theory in Myth and Paradox American Mathematical Society Sylvia Nasar 1998 A Beautiful Mind Simon amp Schuster
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans