Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Kompleks analiz, mürəkkəb dəyişənlərin funksiyalarını öyrənən riyaziyyat sahəsidir. Bu sahə ənənəvi olaraq kompleks dəyişənlərin funksiyaları nəzəriyyəsi kimi də tanınır. Kompleks analiz, ədədlər nəzəriyyəsi, tətbiqi riyaziyyat və fizika daxil olmaqla, riyaziyyatın müxtəlif sahələrində tətbiq olunur. Bununla yanaşı, onun tətbiq sahələri bu ilə məhdudlaşmır.
Kompleks analiz, xüsusilə mürəkkəb dəyişənlərin analitik funksiyaları ilə bağlıdır və bu funksiyalar ümumiyyətlə iki əsas sinifə ayrılır: holomorf funksiyalar və meromorfik funksiyalar. Kompleks analiz, ikiölçülü fizika problemlərində geniş şəkildə tətbiq oluna bilər, çünki hər bir analitik funksiyanın real və xəyali hissələri Laplas tənliyini təmin etməlidir.
Tarixi
Kompleks analiz, 19-cu əsrdən kök salmış bir riyaziyyat sahəsidir, lakin mürəkkəb ədədlərin istifadəsi ilə bağlı düşüncələr 11-ci əsrə və hətta daha əvvəllərə qədər uzanır. Kompleks ədədlərin ilk tətbiqləri 16-cı əsrə, xüsusən də Kardano tərəfindən ikinci və üçüncü dərəcəli tənliklərin həlli zamanı ortaya çıxmışdır. 18-ci və 19-cu əsrlərdə kompleks ədədləri əhatə edən funksiyaları kəşf edən ilk alimlərdən biri Eyler olmuşdur. Kompleks ədədləri ilə bağlı texnikaların inkişafı, real qiymətli funksiyalar nəzəriyyəsində bir çox məsələlərin kompleks ədədlər vasitəsilə daha asan həll olunduğunu göstərmişdir. Bununla yanaşı, kompleks ədədlər hələ də tam olaraq qəbul edilməmişdir. Məsələn, Dekart mürəkkəb kökləri rədd edir və onlara "xəyali" adını vermişdir. Eyler də kompleks ədədlərin "yalnız təsəvvürdə mövcud olduğu" qənaətində idi və mürəkkəb köklərin tənliyin əslində heç bir kökünün olmadığını göstərmək üçün faydalı olduğunu düşünürdü.
Kompleks ədədlərin ümumi qəbulu və kompleks analizin yaranması əsasən Qaussun həndəsi təsviri və kompleks ədədlərin inkişafı ilə başlamışdır. Qaussun işindən sonra kompleks analiz riyaziyyatın yeni və məşhur bir sahəsi kimi formalaşdı və Koşi, Veyerştras və Rieman kimi dövrün məhsuldar riyaziyyatçılarının töhfələri ilə bir çox digər riyazi sahələrlə əlaqələndirilmişdir. Lakin, kompleks analizin yeni sahə kimi yaranmasına baxmayaraq, kompleks ədədlərin ilk tam və riyazi dəqiq ifadəsini Qaussun müasiri Hamilton təqdim etmişdir.
Ənənəvi olaraq, kompleks analiz, xüsusilə açıq istinadlar nəzəriyyəsi ilə, fizikada çoxsaylı tətbiqlərə malikdir. Kompleks analiz həmçinin analitik ədədlər nəzəriyyəsində istifadə olunur. Müasir riyaziyyatda kompleks analiz, fraktal şəkillərin meydana çıxması ilə tanınmışdır; bunlar mürəkkəb dinamika və holomorf funksiyaların təkrarlanması nəticəsində yaranır (bunlardan ən məşhuru Mandelbrot dəstidir). Kompleks analizin müasir vacib tətbiqlərindən biri, açıq-invariant kvant sahə nəzəriyyəsi olan simli nəzəriyyədir. Həmçinin, mühəndislik sahələrində, xüsusilə güc mühəndisliyində, kompleks analiz geniş şəkildə istifadə olunur və tətbiq olunur.
Əhəmiyyəti
Kompleks təhlilin iki əsas əhəmiyyəti və faydası vardır. Birincisi, bu sahə mürəkkəb ədədlərin hesablanması ilə bağlı riyaziyyatın bir uzantısı kimi tanınır. İkincisi, kompleks analiz, real təhlildə geniş yer tuta bilən bir çox problemi unikal üsulları ilə daha qısa və sadə şəkildə həll etməyə imkan tanıyır.
Kompleks funksiyalar
Mürəkkəb funksiya, həm müstəqil dəyişənin, həm də asılı dəyişənin kompleks ədədlər olduğu funksiyadır. Başqa sözlə, kompleks funksiya, domeni kompleks müstəvinin alt çoxluğu və təsvir dəsti də kompleks müstəvinin alt çoxluğu olan bir funksiyadır. Hər bir mürəkkəb funksiyada, həm müstəqil dəyişən, həm də asılı dəyişən, həqiqi və xəyali hissələrə bölünə bilər.
\( x \) və \( y \) real ədədlər olmaqla, \( u(z) \) və \( v(z) \) real qiymətli funksiyalar olaraq qəbul edilir. Burada \( z = x + iy \) və \( w = f(z) = u(z) + iv(z) \) kimi yazılır. Başqa sözlə, \( f(z) \) funksiyasının komponentləri olan \( u = u(x, y) \) və \( v = v(x, y) \) iki real dəyişənin—yəni \( x \) və \( y \)—real qiymətli funksiyaları kimi şərh edilə bilər.
Kompleks analizin əsas anlayışları tez-tez eksponensial, loqarifm və triqonometrik funksiyalar kimi real analizin elementar funksiyalarının kompleks müstəvilərdə genişləndirilməsi ilə əldə edilir.
Törəmələr və Koşi-Riman tənlikləri
Həqiqi analizdə olduğu kimi, "hamar" kompleks funksiya, deyək ki, w = f ( z ) Ω sahəsində müəyyən bir nöqtədə törəmə ola bilər. Əslində törəmənin tərifi belədir
Bir mühüm fərq istisna olmaqla, kompleks analizdə limitin tərifi real vəziyyətdə olduğu kimi qalır. Həqiqi analizdə limit yalnız bir ölçülü ədəd xətti boyunca hərəkət etməklə yaxınlaşmaq mümkündür. Lakin kompleks analizdə limitə iki ölçülü kompleks müstəvidə istənilən istiqamətdən yaxınlaşmaq olar. Bu fərqi istiqamətli törəmələrlə qarışdırmaq olmaz. İstiqamətli törəmələrdə bir ölçülü x xəttində hərəkət etmək mümkündür, lakin bu, diskret vahidlərdə, məsələn, \( y = x^2 \) əyrisi boyunca hərəkət etmək deməkdir; bu, müstəvidə (ölçülü x xəttinin əvəzinə) hərəkət etmək deyil, ona addımlarla yaxınlaşmaqdır.
Əgər bir hədd, yəni törəmə, \( \Omega \) sahəsində hər \( z \) nöqtəsi üçün mövcuddursa, onda \( f(z) \) \( \Omega \) sahəsində diferensiallana bilən funksiyadır. Hər bir diferensiallaşan \( f(z) \) funksiyasının da analitik olduğu sübuta yetirilə bilər. Bu nəticə, həqiqi ədədlərin real qiymətli funksiyaları üçün sübut edilmiş teoremdən daha güclüdür. Həqiqi ədədlərin hesablamasında biz \( f(x) \) funksiyasını qura bilərik ki, onun sahəsində hər yerdə birinci törəməsi var, lakin yalnız bir və ya bir neçə nöqtəsində ikinci törəməsi yoxdur. Lakin, əgər kompleks müstəvidə müəyyən edilmiş kompleks funksiya müəyyən qonşuluqda diferensiallana bilirsə, o, eyni qonşuluqda sonsuz dəfə diferensiallana bilər. (Sübut üçün holomorf funksiyaların analitikliyinə baxın.)
f ( z ), deyək u ( x, y ) və v ( x, y ) təşkil edən iki real funksiyanın qismən törəmələrini hesablamaq üçün vektor hesabı üsullarını tətbiq etməklə və Ω-də z nöqtəsinə aparan iki yolu nəzərə alaraq, mövcudluq törəmə
Bu ifadənin doğru olduğunu göstərmək olar.
Bu iki ifadənin həqiqi və xəyali hissələrini bərabərləşdirməklə Koşi-Riman tənliklərinin ənənəvi formulunu əldə edirik:
![image]()
və ya başqa bir ümumi qeyddə, ![image]()
Bu iki qismən diferensial tənliklər sistemi əvvəlcə x- ə, sonra isə y- ə görə diferensiallaşdırılarsa, aşağıdakı ifadələri asanlıqla göstərmək olar:
![image]()
və ya başqa bir ümumi qeyddə, ![image]()
Başqa sözlə, kompleks dəyişənlərin diferensiallana bilən funksiyasının həqiqi və xəyali hissələri harmonik funksiyalardır .
Həmçinin bax : Laplas tənliyi
Holomorf funksiyalar
Holomorf funksiyalar kompleks müstəvinin açıq alt çoxluğunda fərqlənən mürəkkəb funksiyalardır. Kompleks diferensiallaşma adi real diferensiallaşmadan daha güclü nəticələrə malikdir. Məsələn, bütün real diferensiallanan funksiyalar sonsuz diferensiallana bilmir, holomorf funksiyalar isə sonsuz diferensiallana bilir. Əksər elementar funksiyalar, o cümlədən eksponensial funksiya, triqonometrik funksiyalar və bütün çoxhədlilər holomorfdur.
Ayrıca bakınız: analitik fonksiyon, holomorf demet ve .
Əsas nəticələr
Kompleks analizin nəticələrini bir neçə qrupa bölmək olar. Baxmayaraq ki, hər bir qrupun nəticəsi öz qrupundakı müvafiq nəticələrdən məcmu şəkildə faydalanan mühüm nəticələri ehtiva edir; Lakin bu qrupların hər biri müəyyən əsas nəticələr vasitəsilə bir-biri ilə bağlıdır və bəzi mühüm nəticələr bu əsas qruplara əsaslanır.
İnteqral təsvirlər üzrə nəticələr
Kompleks analizdə mühüm mərkəzi vasitələrdən biri əyrixətti inteqraldır . Bu qapalı yol üzərində qapalı yol ilə məhdudlaşan sahənin hər yerində holomorf olan funksiyanın inteqralı sıfırdır. Bu ifadə həm də Koşi inteqral teoremi kimi tanınır. Dairəvi sahədə (disk) holomorf funksiyanın dəyərləri bu diskdə müəyyən bir əyri (yolu) birləşdirməklə hesablana bilər. Bu ifadə Koşi inteqral düsturu kimi də tanınır.
Həmçinin bax : Morera teoremi
Seriya təmsilləri üzrə nəticələr
Qarışıq real inteqralları həll etmək və müəyyən etmək üçün kompleks müstəvidə əyrixətti inteqrallardan tez-tez istifadə olunur və burada da qalıq nəzəriyyəsi digər nəzəriyyələr arasında ən faydalıdır (bax ). Əgər funksiyanın müəyyən bir nöqtədə qütbü və ya təkliyi varsa, yəni funksiyanın qiymətləri bu nöqtədə qəfil partlayırsa və ya sonlu qiymət almırsa, onda bu funksiyanın bu nöqtədə qalığını hesablamaq olar. bu qütbdə və bu qalıqlar funksiyaya aid əyrixətti inteqralları hesablamaq üçün istifadə edilə bilər. Bu qalıq teoreminin güclü tərəfidir. Əsas təkliklərin yaxınlığında holomorf funksiyaların davranışı Weierstrass-Casorati teoremi ilə müəyyən edilir. Yalnız qütbləri olan, lakin əsas təkliyi olmayan funksiyalara meromorf funksiyalar deyilir. Laurent seriyaları Taylor seriyasına bənzəyir və təkliklərə yaxın funksiyaların davranışını öyrənmək üçün istifadə olunur.
Bütün kompleks müstəvidə holomorf olan məhdud funksiya sabit olmalıdır. Bu ifadə Liouville teoremi kimi tanınır. Bu teorem mürəkkəb ədədlər sahəsinin olduğunu bildirən Cəbrin əsas teoreminin təbii və qısa sübutuna gəlmək üçün istifadə edilə bilər.
Riemann səthlərində nəticələr
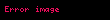Rieman funksiyasının səthiHolomorf funksiyaların başqa bir mühüm xüsusiyyəti odur ki, sadəcə əlaqəli bölgədə holomorf olan funksiyanın dəyərləri tamamilə daha kiçik subregionlardakı dəyərlərlə müəyyən edilə bilər. Böyük bölgədəki funksiya, kiçik bölgədəki funksiyanın qiymətlərinin adlanır. Bu , əvvəlcə yalnız məhdud bir bölgədə birləşən sonsuz cəmlər kimi müəyyən edilmiş Riemann zeta funksiyası kimi bəzi funksiyaların təriflərini demək olar ki, bütün kompleks müstəvidə genişləndirməyə imkan verir. Bəzən təbii loqarifmdə olduğu kimi, holomorf funksiyanı kompleks müstəvidə sadə olmayan əlaqəli bölgəyə analitik şəkildə davam etdirmək mümkün olmur; Bununla belə, onu Riemann səthi adlanan yaxından əlaqəli bir səthə davam etdirmək hələ də mümkündür.
Daha yüksək ölçülərdə nəticələr
Bütün bunlar təkdəyişənli kompleks analizdə etibarlıdır. Bundan əlavə, güc seriyaları kimi analitik xüsusiyyətlər eyni qalır; Bununla belə, açıqlıq kimi bir çox həndəsə xüsusiyyətlərinin tətbiq olunmadığı bir çox mürəkkəb ölçülərdə kompleks təhlilin öyrənildiyi zəngin bir sahəsi də vardır. Birölçülü kompleks analizdə bəlkə də ən mühüm nəticə olan və kompleks müstəvidə müəyyən bölgələrdə koherens əlaqəsini ifadə edən daha yüksək ölçülərdə keçərli deyil.
Həmçinin baxın
- Runge teoremi
- Karmaşık analiz konuları listesi
- Gerçel analiz
Mənbə
- , Vizual Kompleks Təhlil (Oxford, 1997) - Vizual Kompleks Təhlil.
- Henrici P., Tətbiqi və Hesablama Kompleksi Təhlili (Wiley). [Üç cild: 1974, 1977, 1986.]--Tətbiqi və hesablama kompleksi təhlili.
- , Advanced Engineering Mathematics, 9 ed. , Ch.13-18 (Wiley, 2006)--Ali Mühəndislik Riyaziyyatı.
- Scheidemann, V., Bir neçə dəyişənlərdə kompleks analizə giriş (Birkhauser, 2005) - Multivariant kompleks təhlilə giriş.
- Shaw, WT, Mathematica ilə Kompleks Təhlil (Cambridge, 2006) - Mathematica ilə Kompleks Analiz.
- Marsden & Hoffman, Əsas kompleks analiz (Freeman, 1999)--Basic Complex Analysis.
Xarici keçidlər
- Kompleks Təhlil -- Corc Keynin dərsliyi 14 Mart 2009 tarihinde də </link>
- Douglas N. Arnold tərəfindən Kompleks Təhlil kursunun vebsaytı 5 Kasım 2013 tarihinde </link>
- İngilis Vikipediyasında Kompleks Təhlil haqqında nümunə suallar
- Mürəkkəb funksiyaları (və digərlərini) göstərmək üçün istifadə olunan keçidlər toplusu
- John H. Mathews tərəfindən Kompleks Analiz Layihəsi 6 Nisan 2013 tarihinde </link>
- Wolfram Research-in MathWorld Kompleks Təhlil Səhifəsi 11 Kasım 2012 tarihinde </link>
- Complex Viewer- İstənilən mürəkkəb funksiyaya baxmaq üçün istifadə edilən kiçik Java proqram
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Kompleks analiz murekkeb deyisenlerin funksiyalarini oyrenen riyaziyyat sahesidir Bu sahe enenevi olaraq kompleks deyisenlerin funksiyalari nezeriyyesi kimi de taninir Kompleks analiz ededler nezeriyyesi tetbiqi riyaziyyat ve fizika daxil olmaqla riyaziyyatin muxtelif sahelerinde tetbiq olunur Bununla yanasi onun tetbiq saheleri bu ile mehdudlasmir f x x 2 1 x 2 i 2 x 2 2 2 i funksiyasinin qrafiki mahiyyet funksiyasinin arqumentini temsil ederken boyukluyunu temsil edir Kompleks analiz xususile murekkeb deyisenlerin analitik funksiyalari ile baglidir ve bu funksiyalar umumiyyetle iki esas sinife ayrilir holomorf funksiyalar ve meromorfik funksiyalar Kompleks analiz ikiolculu fizika problemlerinde genis sekilde tetbiq oluna biler cunki her bir analitik funksiyanin real ve xeyali hisseleri Laplas tenliyini temin etmelidir TarixiMandelbrot desti fraktal Kompleks analiz 19 cu esrden kok salmis bir riyaziyyat sahesidir lakin murekkeb ededlerin istifadesi ile bagli dusunceler 11 ci esre ve hetta daha evvellere qeder uzanir Kompleks ededlerin ilk tetbiqleri 16 ci esre xususen de Kardano terefinden ikinci ve ucuncu dereceli tenliklerin helli zamani ortaya cixmisdir 18 ci ve 19 cu esrlerde kompleks ededleri ehate eden funksiyalari kesf eden ilk alimlerden biri Eyler olmusdur Kompleks ededleri ile bagli texnikalarin inkisafi real qiymetli funksiyalar nezeriyyesinde bir cox meselelerin kompleks ededler vasitesile daha asan hell olundugunu gostermisdir Bununla yanasi kompleks ededler hele de tam olaraq qebul edilmemisdir Meselen Dekart murekkeb kokleri redd edir ve onlara xeyali adini vermisdir Eyler de kompleks ededlerin yalniz tesevvurde movcud oldugu qenaetinde idi ve murekkeb koklerin tenliyin eslinde hec bir kokunun olmadigini gostermek ucun faydali oldugunu dusunurdu Kompleks ededlerin umumi qebulu ve kompleks analizin yaranmasi esasen Qaussun hendesi tesviri ve kompleks ededlerin inkisafi ile baslamisdir Qaussun isinden sonra kompleks analiz riyaziyyatin yeni ve meshur bir sahesi kimi formalasdi ve Kosi Veyerstras ve Rieman kimi dovrun mehsuldar riyaziyyatcilarinin tohfeleri ile bir cox diger riyazi sahelerle elaqelendirilmisdir Lakin kompleks analizin yeni sahe kimi yaranmasina baxmayaraq kompleks ededlerin ilk tam ve riyazi deqiq ifadesini Qaussun muasiri Hamilton teqdim etmisdir Enenevi olaraq kompleks analiz xususile aciq istinadlar nezeriyyesi ile fizikada coxsayli tetbiqlere malikdir Kompleks analiz hemcinin analitik ededler nezeriyyesinde istifade olunur Muasir riyaziyyatda kompleks analiz fraktal sekillerin meydana cixmasi ile taninmisdir bunlar murekkeb dinamika ve holomorf funksiyalarin tekrarlanmasi neticesinde yaranir bunlardan en meshuru Mandelbrot destidir Kompleks analizin muasir vacib tetbiqlerinden biri aciq invariant kvant sahe nezeriyyesi olan simli nezeriyyedir Hemcinin muhendislik sahelerinde xususile guc muhendisliyinde kompleks analiz genis sekilde istifade olunur ve tetbiq olunur EhemiyyetiKompleks tehlilin iki esas ehemiyyeti ve faydasi vardir Birincisi bu sahe murekkeb ededlerin hesablanmasi ile bagli riyaziyyatin bir uzantisi kimi taninir Ikincisi kompleks analiz real tehlilde genis yer tuta bilen bir cox problemi unikal usullari ile daha qisa ve sade sekilde hell etmeye imkan taniyir Kompleks funksiyalarMurekkeb funksiya hem musteqil deyisenin hem de asili deyisenin kompleks ededler oldugu funksiyadir Basqa sozle kompleks funksiya domeni kompleks mustevinin alt coxlugu ve tesvir desti de kompleks mustevinin alt coxlugu olan bir funksiyadir Her bir murekkeb funksiyada hem musteqil deyisen hem de asili deyisen heqiqi ve xeyali hisselere bolune biler x ve y real ededler olmaqla u z ve v z real qiymetli funksiyalar olaraq qebul edilir Burada z x iy ve w f z u z iv z kimi yazilir Basqa sozle f z funksiyasinin komponentleri olan u u x y ve v v x y iki real deyisenin yeni x ve y real qiymetli funksiyalari kimi serh edile biler Kompleks analizin esas anlayislari tez tez eksponensial loqarifm ve triqonometrik funksiyalar kimi real analizin elementar funksiyalarinin kompleks mustevilerde genislendirilmesi ile elde edilir Toremeler ve Kosi Riman tenlikleriHeqiqi analizde oldugu kimi hamar kompleks funksiya deyek ki w f z W sahesinde mueyyen bir noqtede toreme ola biler Eslinde toremenin terifi beledir f z dwdz limh 0f z h f z h displaystyle f prime z frac dw dz lim h to 0 frac f z h f z h Bir muhum ferq istisna olmaqla kompleks analizde limitin terifi real veziyyetde oldugu kimi qalir Heqiqi analizde limit yalniz bir olculu eded xetti boyunca hereket etmekle yaxinlasmaq mumkundur Lakin kompleks analizde limite iki olculu kompleks mustevide istenilen istiqametden yaxinlasmaq olar Bu ferqi istiqametli toremelerle qarisdirmaq olmaz Istiqametli toremelerde bir olculu x xettinde hereket etmek mumkundur lakin bu diskret vahidlerde meselen y x 2 eyrisi boyunca hereket etmek demekdir bu mustevide olculu x xettinin evezine hereket etmek deyil ona addimlarla yaxinlasmaqdir Eger bir hedd yeni toreme Omega sahesinde her z noqtesi ucun movcuddursa onda f z Omega sahesinde diferensiallana bilen funksiyadir Her bir diferensiallasan f z funksiyasinin da analitik oldugu subuta yetirile biler Bu netice heqiqi ededlerin real qiymetli funksiyalari ucun subut edilmis teoremden daha gucludur Heqiqi ededlerin hesablamasinda biz f x funksiyasini qura bilerik ki onun sahesinde her yerde birinci toremesi var lakin yalniz bir ve ya bir nece noqtesinde ikinci toremesi yoxdur Lakin eger kompleks mustevide mueyyen edilmis kompleks funksiya mueyyen qonsuluqda diferensiallana bilirse o eyni qonsuluqda sonsuz defe diferensiallana biler Subut ucun holomorf funksiyalarin analitikliyine baxin f z deyek u x y ve v x y teskil eden iki real funksiyanin qismen toremelerini hesablamaq ucun vektor hesabi usullarini tetbiq etmekle ve W de z noqtesine aparan iki yolu nezere alaraq movcudluq toreme f z u x i v x v y i u y displaystyle f prime z frac partial u partial x i frac partial v partial x frac partial v partial y i frac partial u partial y Bu ifadenin dogru oldugunu gostermek olar Bu iki ifadenin heqiqi ve xeyali hisselerini beraberlesdirmekle Kosi Riman tenliklerinin enenevi formulunu elde edirik u x v y u y v x displaystyle frac partial u partial x frac partial v partial y qquad frac partial u partial y frac partial v partial x ve ya basqa bir umumi qeydde ux vyuy vx displaystyle u x v y qquad u y v x Bu iki qismen diferensial tenlikler sistemi evvelce x e sonra ise y e gore diferensiallasdirilarsa asagidaki ifadeleri asanliqla gostermek olar 2u x2 2u y2 0 2v x2 2v y2 0 displaystyle frac partial 2 u partial x 2 frac partial 2 u partial y 2 0 qquad frac partial 2 v partial x 2 frac partial 2 v partial y 2 0 ve ya basqa bir umumi qeydde uxx uyy vxx vyy 0 displaystyle u xx u yy v xx v yy 0 Basqa sozle kompleks deyisenlerin diferensiallana bilen funksiyasinin heqiqi ve xeyali hisseleri harmonik funksiyalardir Hemcinin bax Laplas tenliyiHolomorf funksiyalarHolomorf funksiyalar kompleks mustevinin aciq alt coxlugunda ferqlenen murekkeb funksiyalardir Kompleks diferensiallasma adi real diferensiallasmadan daha guclu neticelere malikdir Meselen butun real diferensiallanan funksiyalar sonsuz diferensiallana bilmir holomorf funksiyalar ise sonsuz diferensiallana bilir Ekser elementar funksiyalar o cumleden eksponensial funksiya triqonometrik funksiyalar ve butun coxhedliler holomorfdur Ayrica bakiniz analitik fonksiyon holomorf demet ve Esas neticelerKompleks analizin neticelerini bir nece qrupa bolmek olar Baxmayaraq ki her bir qrupun neticesi oz qrupundaki muvafiq neticelerden mecmu sekilde faydalanan muhum neticeleri ehtiva edir Lakin bu qruplarin her biri mueyyen esas neticeler vasitesile bir biri ile baglidir ve bezi muhum neticeler bu esas qruplara esaslanir Inteqral tesvirler uzre neticeler Kompleks analizde muhum merkezi vasitelerden biri eyrixetti inteqraldir Bu qapali yol uzerinde qapali yol ile mehdudlasan sahenin her yerinde holomorf olan funksiyanin inteqrali sifirdir Bu ifade hem de Kosi inteqral teoremi kimi taninir Dairevi sahede disk holomorf funksiyanin deyerleri bu diskde mueyyen bir eyri yolu birlesdirmekle hesablana biler Bu ifade Kosi inteqral dusturu kimi de taninir Hemcinin bax Morera teoremi Seriya temsilleri uzre neticeler Qarisiq real inteqrallari hell etmek ve mueyyen etmek ucun kompleks mustevide eyrixetti inteqrallardan tez tez istifade olunur ve burada da qaliq nezeriyyesi diger nezeriyyeler arasinda en faydalidir bax Eger funksiyanin mueyyen bir noqtede qutbu ve ya tekliyi varsa yeni funksiyanin qiymetleri bu noqtede qefil partlayirsa ve ya sonlu qiymet almirsa onda bu funksiyanin bu noqtede qaligini hesablamaq olar bu qutbde ve bu qaliqlar funksiyaya aid eyrixetti inteqrallari hesablamaq ucun istifade edile biler Bu qaliq teoreminin guclu terefidir Esas tekliklerin yaxinliginda holomorf funksiyalarin davranisi Weierstrass Casorati teoremi ile mueyyen edilir Yalniz qutbleri olan lakin esas tekliyi olmayan funksiyalara meromorf funksiyalar deyilir Laurent seriyalari Taylor seriyasina benzeyir ve tekliklere yaxin funksiyalarin davranisini oyrenmek ucun istifade olunur Butun kompleks mustevide holomorf olan mehdud funksiya sabit olmalidir Bu ifade Liouville teoremi kimi taninir Bu teorem murekkeb ededler sahesinin oldugunu bildiren Cebrin esas teoreminin tebii ve qisa subutuna gelmek ucun istifade edile biler Riemann sethlerinde neticeler f z z displaystyle f z sqrt z Rieman funksiyasinin sethi Holomorf funksiyalarin basqa bir muhum xususiyyeti odur ki sadece elaqeli bolgede holomorf olan funksiyanin deyerleri tamamile daha kicik subregionlardaki deyerlerle mueyyen edile biler Boyuk bolgedeki funksiya kicik bolgedeki funksiyanin qiymetlerinin adlanir Bu evvelce yalniz mehdud bir bolgede birlesen sonsuz cemler kimi mueyyen edilmis Riemann zeta funksiyasi kimi bezi funksiyalarin teriflerini demek olar ki butun kompleks mustevide genislendirmeye imkan verir Bezen tebii loqarifmde oldugu kimi holomorf funksiyani kompleks mustevide sade olmayan elaqeli bolgeye analitik sekilde davam etdirmek mumkun olmur Bununla bele onu Riemann sethi adlanan yaxindan elaqeli bir sethe davam etdirmek hele de mumkundur Daha yuksek olculerde neticeler Butun bunlar tekdeyisenli kompleks analizde etibarlidir Bundan elave guc seriyalari kimi analitik xususiyyetler eyni qalir Bununla bele aciqliq kimi bir cox hendese xususiyyetlerinin tetbiq olunmadigi bir cox murekkeb olculerde kompleks tehlilin oyrenildiyi zengin bir sahesi de vardir Birolculu kompleks analizde belke de en muhum netice olan ve kompleks mustevide mueyyen bolgelerde koherens elaqesini ifade eden daha yuksek olculerde kecerli deyil Hemcinin baxinRunge teoremi Karmasik analiz konulari listesi Gercel analizMenbe Vizual Kompleks Tehlil Oxford 1997 Vizual Kompleks Tehlil Henrici P Tetbiqi ve Hesablama Kompleksi Tehlili Wiley Uc cild 1974 1977 1986 Tetbiqi ve hesablama kompleksi tehlili Advanced Engineering Mathematics 9 ed Ch 13 18 Wiley 2006 Ali Muhendislik Riyaziyyati Scheidemann V Bir nece deyisenlerde kompleks analize giris Birkhauser 2005 Multivariant kompleks tehlile giris Shaw WT Mathematica ile Kompleks Tehlil Cambridge 2006 Mathematica ile Kompleks Analiz Marsden amp Hoffman Esas kompleks analiz Freeman 1999 Basic Complex Analysis Xarici kecidlerKompleks Tehlil Corc Keynin dersliyi 14 Mart 2009 tarihinde de lt link gt Douglas N Arnold terefinden Kompleks Tehlil kursunun vebsayti 5 Kasim 2013 tarihinde lt link gt Ingilis Vikipediyasinda Kompleks Tehlil haqqinda numune suallar Murekkeb funksiyalari ve digerlerini gostermek ucun istifade olunan kecidler toplusu John H Mathews terefinden Kompleks Analiz Layihesi 6 Nisan 2013 tarihinde lt link gt Wolfram Research in MathWorld Kompleks Tehlil Sehifesi 11 Kasim 2012 tarihinde lt link gt Complex Viewer Istenilen murekkeb funksiyaya baxmaq ucun istifade edilen kicik Java proqram