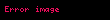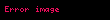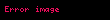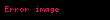Eyler düsturu Leonard Eyler tərəfindən daxil edilmiş və onun şərəfinə adlandırılmış, kompleks triqonometrik funksiyalarla əlaqələndirən düstur.

Eyler düsturu iddia edir ki, istənilən həqiqi ədəd üçün aşağıdakı bərabərlik doğrudur:
- ,
burada — natural loqarifmanın əsası,
- — xəyali vahid.
Törəmə düsturlar
Eyler düsturunun köməyi ilə 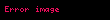

,
.
Sonra triqonometrik funksiyalara kompleks dəyişən daxil etmək olar. Tutaq ki, 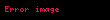
,
.
Beş fundamental riyazi sabiti birləşdirən məşhur Eyler eyniliyi:
Eyler eyniliyinin təsadüfi hissəsidir.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Eyler dusturu Leonard Eyler terefinden daxil edilmis ve onun serefine adlandirilmis kompleks triqonometrik funksiyalarla elaqelendiren dustur Eyler dusturunun hendesi menasi Eyler dusturu iddia edir ki istenilen heqiqi eded x displaystyle x ucun asagidaki beraberlik dogrudur eix cos x isin x displaystyle e ix cos x i sin x burada e displaystyle e natural loqarifmanin esasi i displaystyle i xeyali vahid Toreme dusturlarEyler dusturunun komeyi ile sin displaystyle sin ve cos displaystyle cos funksiyalari asagidaki qaydada teyin etmek olar sin x eix e ix2i displaystyle sin x frac e ix e ix 2i cos x eix e ix2 displaystyle cos x frac e ix e ix 2 Sonra triqonometrik funksiyalara kompleks deyisen daxil etmek olar Tutaq ki x iy displaystyle x iy onda sin iy e y ey2i ishy displaystyle sin iy frac e y e y 2i i mathop mathrm sh y cos iy e y ey2 chy displaystyle cos iy frac e y e y 2 mathop mathrm ch y Bes fundamental riyazi sabiti birlesdiren meshur Eyler eyniliyi eip 1 0 displaystyle e i pi 1 0 x p displaystyle x pi Eyler eyniliyinin tesadufi hissesidir dd Riyaziyyat ile elaqedar bu meqale qaralama halindadir Meqaleni redakte ederek Vikipediyani zenginlesdirin Etdiyiniz redakteleri menbe ve istinadlarla esaslandirmagi unutmayin
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State