Elastiklik qüvvəsi — deformasiya zamanı yaranan qüvvə. Qüvvənin növündən asılı olaraq cismə tətbiq olunan qüvvə ona təcil verir, yaxud cismi deformasiyaya uğradır (ölçü və formanı dəyişdirir). Qüvvənin təsiri ilə baş verən deformasiyaya nəzər salaq. Qüvvənin təsiri kəsildikdən sonra cismin ilk ölçüsünün və formasının bərpa olunma dərəcəsinə görə iki növ deformasiyaya rast gəlinir. Təsir kəsildikdən sonra cisim tamamilə ilk ölçü və formasını alırsa, baş vermiş deformasiya elastiki deformasiya adlanır. Təcrübi faktlarla müəyyən olunmuşdur ki, elastiki deformasiya cismin fərdi xüsusiyyətindən asılı olmaqla yanaşı təsir edən qüvvənin müəyyən qiymətləri intervalında baş verir. Qüvvənin müəyyən qiymətindən sonra təsirin kəsilməsinə baxmayaraq cisim tam mənada ilk halına qayıda bilmir. Elə maddələr vardır ki, onlarda hətta çox kiçik qüvvənin təsiri ilə meydana gələn deformasiya təsir kəsildikdən sonra bərpa olunmur. Bu növ deformasiyalar plastik deformasiya adlanır. Plastik deformasiyanı yaradan qüvvənin ən kiçik qiyməti (yaxud, elastiki deformasiyanı yaradan qüvvənin mümkün olan ən böyük qiyməti) müxtəlif cisimlər üçün müxtəlifdir. Qüvvələrin tətbiq olunma üsuluna görə bərk cisimlərdə müxtəlif növ elastik deformasiyalar - dartılma (yaxud sıxılma), sürüşmə və burulma deformasiyaları baş verir.
Dartılma (sıxılma) deformasiyası

Ən sadə dartılma deformasiyası cismə bir düz xətt istiqamətində yönələn qüvvə tətbiq etməklə müşahidə olunur. Belə dartılma deformasiyası uzununa, yaxud biroxlu dartılma deformasiyası adlanır (Şəkil 1). Uzununa deformasiyanı kəmiyyətcə xarakterizə etmək üçün bircins izotrop materialdan hazırlanmış milin uclarına ox boyu əks istiqamətlərə yönəlmiş bərabər 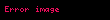
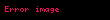
Deformasiyanı xarici qüvvənin təsiri nəticəsində əldə olunan uzanma ilə xarakterizə etmək olar. Nümunənin ilk uzunluğu 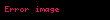

deformasiya 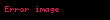
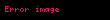
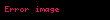
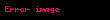
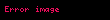
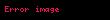
Burada 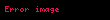
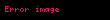
Təcrübi faktlarla müəyyən olunmuşdur ki, nisbi deformasiya nümunənin vahid en kəsiyinə təsir edən qüvvə ilə düz mütənasibdir:
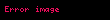




Huk qanunu
Qüvvə en kəsiyə perpendikulyar istiqamətdə yönəldikdə gərginlik (nümunənin vahid en kəsiyinə perpendikulyar istiqamətdə təsir edən qüvvə)

ifadəsi ilə təyin olunur. (3)-ü (2)-də nəzərə alsaq

(4) ifadəsi Huk qanunu adlanır. (4) ifadəsində 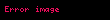
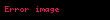
(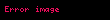

Yunq moldulu
Maddənin elastiklik xassəsi elastiklik əmsalı ilə yanaşı onun tərs qiyməti olan 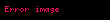
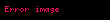
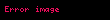
alınır. (1)-i (5)-də nəzərə alaraq Yunq modulunu təyin edək:

(6)-dan göründüyü kimi 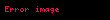
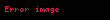
bərabərdir. Nisbi uzanmanın 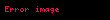

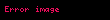
İstinadlar
- N.M.Qocayev Ümumi Fizika Kursu I cild Mexanika Bakı,2011
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Elastiklik quvvesi deformasiya zamani yaranan quvve Quvvenin novunden asili olaraq cisme tetbiq olunan quvve ona tecil verir yaxud cismi deformasiyaya ugradir olcu ve formani deyisdirir Quvvenin tesiri ile bas veren deformasiyaya nezer salaq Quvvenin tesiri kesildikden sonra cismin ilk olcusunun ve formasinin berpa olunma derecesine gore iki nov deformasiyaya rast gelinir Tesir kesildikden sonra cisim tamamile ilk olcu ve formasini alirsa bas vermis deformasiya elastiki deformasiya adlanir Tecrubi faktlarla mueyyen olunmusdur ki elastiki deformasiya cismin ferdi xususiyyetinden asili olmaqla yanasi tesir eden quvvenin mueyyen qiymetleri intervalinda bas verir Quvvenin mueyyen qiymetinden sonra tesirin kesilmesine baxmayaraq cisim tam menada ilk halina qayida bilmir Ele maddeler vardir ki onlarda hetta cox kicik quvvenin tesiri ile meydana gelen deformasiya tesir kesildikden sonra berpa olunmur Bu nov deformasiyalar plastik deformasiya adlanir Plastik deformasiyani yaradan quvvenin en kicik qiymeti yaxud elastiki deformasiyani yaradan quvvenin mumkun olan en boyuk qiymeti muxtelif cisimler ucun muxtelifdir Quvvelerin tetbiq olunma usuluna gore berk cisimlerde muxtelif nov elastik deformasiyalar dartilma yaxud sixilma surusme ve burulma deformasiyalari bas verir Dartilma sixilma deformasiyasiSekil 1 Uzununa deformasiya En sade dartilma deformasiyasi cisme bir duz xett istiqametinde yonelen quvve tetbiq etmekle musahide olunur Bele dartilma deformasiyasi uzununa yaxud biroxlu dartilma deformasiyasi adlanir Sekil 1 Uzununa deformasiyani kemiyyetce xarakterize etmek ucun bircins izotrop materialdan hazirlanmis milin uclarina ox boyu eks istiqametlere yonelmis beraber f1 displaystyle f 1 ve f2 displaystyle f 2 quvvelerini tetbiq edek Sekil 2 Quvvelerin istiqametlerinden asili olaraq mil uzanir Sekil 2 a ve ya sixilir Sekil 2 b Deformasiyani xarici quvvenin tesiri neticesinde elde olunan uzanma ile xarakterize etmek olar Numunenin ilk uzunlugu l0 displaystyle l 0 son uzunlugu ise l olarsa Sekil 2 Cisimlerin uzununa deformasiyasini mueyyen eden kemiyyetler deformasiya l l l0 displaystyle bigtriangleup l l l 0 olur Buradaki l displaystyle bigtriangleup l mutleq deformasiya adlanir Mutleq deformasiya numunenin elastiklik xassesini tam xarakterize etmir Cunki onun qiymetinin boyuk olmasi hele numunenin yuksek derecede elastiki olmasindan xeber vermir Bunu daha eyani tesevvur etmek ucun bele bir misala nezer salaq Tutaq ki elastiki xasseleri bir birine cox yaxin olan iki numune vardir Bunlardan birinin uzunlugu l0 displaystyle l 0 digerinin uzunlugu ise bundan 5 defe boyukdur Birinci numune ikinciye nezeren daha elastikdir Eyni quvvenin tesiri neticesinde yaranan mutleq deformasiyalar bele olar l1 lt l2 displaystyle bigtriangleup l 1 lt bigtriangleup l 2 yeni ikinci numune daha cox uzanmisdir Lakin bu ikinci numunenin birinciyenezeren daha elastiki olmasinin neticesi deyildir cunki elastikliyi nisbeten az olan ikinci numune birinciden 5 defe uzundur Demeli mutleq deformasiya cismin elasiklik xassesini tam xarakterize etmir Numunelerin uzunluqlari eyni olsaydi tebiidir ki elastikliyi daha boyuk olanin mutleq deformasiyasi nisbeten boyuk olardi Buradan aydin olur ki cismin deformasiya qabiliyyeti onun vahid uzunluguna dusen mutleq deformasiya ile tam xarakterize olunur Bu kemiyyet yeni vahid uzunluga dusen mutleq deformasiyaya nisbi uzanma e displaystyle varepsilon deyilir e ll displaystyle varepsilon frac vartriangle l l 1 Burada l displaystyle l numunenin ilk uzunlugu l displaystyle bigtriangleup l ise mutleq uzanmadir 1 ifadesinde numunenin beraber uzunluqda goturulmus ixtiyari hissesinin uzanmasinin eyni oldugu nezere alinmisdir Buna sebeb numunenin bircins olmasi ve ona gore de tesirin onun en kesiyi boyunca beraber paylanmasidir Tecrubi faktlarla mueyyen olunmusdur ki nisbi deformasiya numunenin vahid en kesiyine tesir eden quvve ile duz mutenasibdir e afS displaystyle varepsilon alpha frac f S 2 S displaystyle S numunenin en kesiyinin sahesi f displaystyle f en kesiyine tesir eden quvve a displaystyle alpha mutenasiblik emsalidir a displaystyle alpha emsali numunenin elastikliyini xarakterize etdiyinden elastiklik emsali adlanir 2 ifadesi yalniz elastiki deformasiya hududunda dogrudur Huk qanunuQuvve en kesiye perpendikulyar istiqametde yoneldikde gerginlik numunenin vahid en kesiyine perpendikulyar istiqametde tesir eden quvve sn fS displaystyle sigma n frac f S 3 ifadesi ile teyin olunur 3 u 2 de nezere alsaq e a sn displaystyle varepsilon alpha centerdot sigma n 4 4 ifadesi Huk qanunu adlanir 4 ifadesinde sn 1 displaystyle sigma n 1 olduqda a e displaystyle alpha varepsilon alinir Bu ise o demekdir ki elastiklik emsali ededi qiymetce vahid gerginliyin sn 1 displaystyle sigma n 1 yaratdigi nisbi uzanmaya e displaystyle varepsilon beraberdir Yunq molduluMaddenin elastiklik xassesi elastiklik emsali ile yanasi onun ters qiymeti olan 1a E displaystyle frac 1 alpha E kemiyyeti ile de xarakterize olunur Bu kemiyyet Yunq modulu adlanir 4 ifadesinde 1a E displaystyle frac 1 alpha E yazsaq e snE displaystyle varepsilon frac sigma n E 5 alinir 1 i 5 de nezere alaraq Yunq modulunu teyin edek E sn l l displaystyle E frac sigma n vartriangle l l 6 6 dan gorunduyu kimi l l 1 displaystyle vartriangle l l 1 olduqda E sn displaystyle E sigma n alinir basqa sozle Yunq modulu ededi qiymetce vahid nisbi uzanma yaradan normal gerginliye beraberdir Nisbi uzanmanin l l 1 displaystyle vartriangle l l 1 olmasi sertinden ls l l 1 displaystyle l s l l 1 ve buradan ls 2l displaystyle l s 2l aliriq Demeli Yunq modulu ededi qiymetce numuneni iki defe uzada bilen normal gerginliye beraberdir IstinadlarN M Qocayev Umumi Fizika Kursu I cild Mexanika Baki 2011
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans