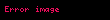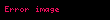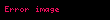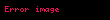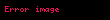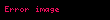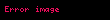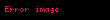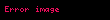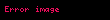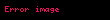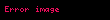Dispersiya analizi bir və ya bir neçə asılı göstəricilər ilə bir və ya bir neçə asılı olmayan parametrlər arasında münasibətin analizinə xidmət edir. Bu yoxlama üsulu prosesin giriş parametri və çıxış göstəriciləri arasında mövcud olan asılılığın aşkar edilməsi üçün zəmin yaradır. Ona riyazi statistikada çox vaxt struktur yoxlanması da deyilir. Dispersiya analizi eksperimentlərin planlanmasının əsası sayılır.
Dispersiya analizi təsadüfi metrik dəyişənlərin müxtəlif qruplardakı (həmçinin siniflərdə) riyazi gözləməsinin fərqlənməsini yoxlayır. Yoxlama üsulu ilə qruplar arasında yaranan dispersiya ilə qrup daxili dispersiya arasındakı fərqin böyük olub-olmaması dəqiqləşdirilir. Bunun sayəsində qrupların bölünməsinin əhəmiyyətli və ya əhəmiyyətsiz olmasını görmək olur. Əgər qruplar arasındakı fərq böyük olarsa, onda ehtimal olunur ki, onlara müxtəlif qanunauyğunluqlar təsir edir. Digər tərəfdən nəzarət qrupunun eksperiment qrupu ilə identik olması aydınlaşdırılır. Dispersiya analizinin növü faktorların sayı ilə müəyyən edilir. Bir asılı olmayan parametrin bir asılı olan göstəriciyə təsiri araşdırılırsa buna bir faktorlu disperisya analizi deyilir. İki və çoxfaktorlu dispersiya analizi də aparılır. Dispersiyanın iki faktorlu təsirdə analizinin riyazi təsviri aşağıda verilmişdir. Əgər naməlum sabitlər a1,...., an müxtəlif üsullarla və ya cihazlarla (M1,..., Мm ) ölçülə bilirsə və hər bir ölçmədə təsadüfi xəta həm seçilmiş üsuldan, həm də naməlum ölçülən qiymətdən (ai ) asılı olarsa, onda ölçmənin nəticələri xij aşağıdakı cəm şəklində göstərilə bilər:
,
i=1,2,..,n; j=1,2,..., m.
burada: bij — ai parametrini Mj üsulu ilə ölçmədə yaranan sistematik xətadır, dij —təsadüfi xətadır. Bu model ikifaktorlu sxemə malik dispersiya analizidir (birinci faktor ölçülən parametr, ikinci isə ölçmə üsuludur). Təsadüfi qiymətlər çoxluğuna uyğun emprik paylanmanın dispersiyası olur
, , ,
burada:
aşağıdakı düsturla ifadə olunur:
Bu dispersiyalar
bərabərliyini ödəyirlər. Dispersiya analizinin adı da buradan yaranmışdır. Əgər sistematik xətalar ölçmə üsulundn asılı deyilsə, onda s22/s20 vahidə yaxınlaşır. Bu xassə sistematik fərqləndirmə üçün əsas meyyar sayılır. Əgər s22/s02 nisbəti vahiddən əhəmiyyətli dərəcədə fərqlənərsə, onda sistematik xətaların fərqinin yoxluğu hipotezası qəbul edilmir. Fərqlənmənin qiyməti ölçmənin təsadüfi xətalarının ehtimalının paylanması qanununa uyğun təyin edilir. Ölçmə dəqiqliyinin həmişə sabit qalması və təsadüfi xətaların normal paylanma qanununa tabe olmasının xüsusi halında s22/s20 üçün kritik qiymət F-paylanamsının köməyi ilə aparılır. Burada izah olunmuş ardıcıl analiz yalnız sistematik fərqlərin olmasını öyrənməyə kömək edir. O, kənar amillərin ölçmənin nəticələrinə təsirininin kəmiyyətcə qiymətləndirilməsi üçün yararlı deyil. Bu məqsədə yalnız ölçmənin dəfələrlə təkrarlanması ilə çatmaq olar.
İstinadlar
- Rezo Əliyev. Maşınqayırma leksikonu. II hissə, Bakı: Appostrof nəşriyyatı, 2012, 427 s.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Dispersiya analizi bir ve ya bir nece asili gostericiler ile bir ve ya bir nece asili olmayan parametrler arasinda munasibetin analizine xidmet edir Bu yoxlama usulu prosesin giris parametri ve cixis gostericileri arasinda movcud olan asililigin askar edilmesi ucun zemin yaradir Ona riyazi statistikada cox vaxt struktur yoxlanmasi da deyilir Dispersiya analizi eksperimentlerin planlanmasinin esasi sayilir Dispersiya analizi tesadufi metrik deyisenlerin muxtelif qruplardaki hemcinin siniflerde riyazi gozlemesinin ferqlenmesini yoxlayir Yoxlama usulu ile qruplar arasinda yaranan dispersiya ile qrup daxili dispersiya arasindaki ferqin boyuk olub olmamasi deqiqlesdirilir Bunun sayesinde qruplarin bolunmesinin ehemiyyetli ve ya ehemiyyetsiz olmasini gormek olur Eger qruplar arasindaki ferq boyuk olarsa onda ehtimal olunur ki onlara muxtelif qanunauygunluqlar tesir edir Diger terefden nezaret qrupunun eksperiment qrupu ile identik olmasi aydinlasdirilir Dispersiya analizinin novu faktorlarin sayi ile mueyyen edilir Bir asili olmayan parametrin bir asili olan gostericiye tesiri arasdirilirsa buna bir faktorlu disperisya analizi deyilir Iki ve coxfaktorlu dispersiya analizi de aparilir Dispersiyanin iki faktorlu tesirde analizinin riyazi tesviri asagida verilmisdir Eger namelum sabitler a1 an muxtelif usullarla ve ya cihazlarla M1 Mm olcule bilirse ve her bir olcmede tesadufi xeta hem secilmis usuldan hem de namelum olculen qiymetden ai asili olarsa onda olcmenin neticeleri xij asagidaki cem seklinde gosterile biler xi j ai bi j di j displaystyle x i j a i b i j d i j i 1 2 n j 1 2 m burada bij ai parametrini Mj usulu ile olcmede yaranan sistematik xetadir dij tesadufi xetadir Bu model ikifaktorlu sxeme malik dispersiya analizidir birinci faktor olculen parametr ikinci ise olcme usuludur Tesadufi qiymetler coxluguna uygun emprik paylanmanin dispersiyasi olur xi j displaystyle x i j xi j xi x j x displaystyle x i j x i x j x xi displaystyle x i x j displaystyle x j burada x j 1n ixi j displaystyle x j frac 1 n sum i x i j xi 1m jxi j displaystyle x i frac 1 m sum j x i j x 1nm i jxi j displaystyle x frac 1 nm sum i j x i j asagidaki dusturla ifade olunur s2 1nm i j xi j x 2 displaystyle s 2 frac 1 nm sum i sum j x i j x 2 s02 1nm i j xi j xi x j x 2 displaystyle s 0 2 frac 1 nm sum i sum j x i j x i x j x 2 s12 1n i xi x 2 displaystyle s 1 2 frac 1 n sum i x i x 2 s22 1m j x j x 2 displaystyle s 2 2 frac 1 m sum j x j x 2 Bu dispersiyalar s2 s02 s12 s22 displaystyle s 2 s 0 2 s 1 2 s 2 2 beraberliyini odeyirler Dispersiya analizinin adi da buradan yaranmisdir Eger sistematik xetalar olcme usulundn asili deyilse onda s22 s20 vahide yaxinlasir Bu xasse sistematik ferqlendirme ucun esas meyyar sayilir Eger s22 s02 nisbeti vahidden ehemiyyetli derecede ferqlenerse onda sistematik xetalarin ferqinin yoxlugu hipotezasi qebul edilmir Ferqlenmenin qiymeti olcmenin tesadufi xetalarinin ehtimalinin paylanmasi qanununa uygun teyin edilir Olcme deqiqliyinin hemise sabit qalmasi ve tesadufi xetalarin normal paylanma qanununa tabe olmasinin xususi halinda s22 s20 ucun kritik qiymet F paylanamsinin komeyi ile aparilir Burada izah olunmus ardicil analiz yalniz sistematik ferqlerin olmasini oyrenmeye komek edir O kenar amillerin olcmenin neticelerine tesirininin kemiyyetce qiymetlendirilmesi ucun yararli deyil Bu meqsede yalniz olcmenin defelerle tekrarlanmasi ile catmaq olar IstinadlarRezo Eliyev Masinqayirma leksikonu II hisse Baki Appostrof nesriyyati 2012 427 s
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State