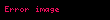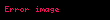VKB metodu (Ventzel-Kramers-Brillüen) – Kvant mexanikasında kvaziklassik yaxınlaşmadır. Bu metod , və arasında əlaqə qurur, belə ki, dalğa funksiyası klassik təsir vasitəsilə ifadə olunur. Bu metod 1926-ci ildə bir-birindən asılı olmadan üç fizik Q.Ventzel, H.Kramers və L.Brillüenin tərəfindən inkişaf etdirildiyinə görə VKB metodu adını almışdır.
Şredinger tənliyini yazaq:
Burada potensialının nöqtəsində minimumunun olduğu və bu nöqtədən uzaqlaşdıqca monoton artdığı nəzərdə tutulur. Belə potensialda enerjisinə malik klassik zərrəcik (maddi nöqtə) tənliyinin həlləri olan və nöqtələri arasında periodik rəqs edəcək. Yeni dəyişənlər daxil edək
və Şredinger tənliyini yenidən yazaq:
Dalğa funksiyasını aşağıdakı şəkildə göstərək:
burada amplitud və eksponentin qüvvəti həqiqi nəzərdə tutulurlar. Sonuncu ifadəni Şredinger tənliyində nəzərə alsaq aşağıdakı alarıq:
burada lokal impulsdur. Alınmış tənliklər Şredinger tənliyinə tam ekvivalentdirlər. Kvaziklassik yaxınlaşmada həddi kiçik olduğu üçün atıla bilər (bu yazınlaşmasız qeyri-xətti Rikkati tənliyi dəqiq həll olunmur). Bu halda alınan ifadələri inteqrallamaq olur:
burada klassik təsirə uyğun gəlir. Nəticədə kvaziklassik tapmış oluruq:
Təsvir olunan bu metod VKB metodu adlanır.
Xarici keçidlər
- [1][ölü keçid] – S. C. Miller, Jr. and R. H. Good, Jr. A WKB-Type Approximation to the Schrödinger Equation Phys. Rev. 91, 174–179 (1953)
- [2][ölü keçid] – Carl M. Bender, G. S. Guralnik, Martin L. Silverstein WKB approximation for quantum theory on a lattice Phys. Rev. D 20, 2583–2591 (1979)
- [3][ölü keçid] – Abraham Klein and H. Arthur Weldon Equations of motion, variational principles, and WKB approximations in quantum mechanics and quantum field theory: Bound states Phys. Rev. D 17, 1009–1030 (1977)
- [4][ölü keçid] – Gua Xiao-Yan and Sun Jian-Qiang Notes on Application of WKB Method Commun. Theor. Phys. 50 864-866 (2008)
İstinadlar
- Wentzel, Gregor (1926). "Eine Verallgemeinerung der Quantenbedingungen für die Zwecke der Wellenmechanik". Zeitschrift der Physik 38: 518–529
- Kramers, Hendrik A. (1926). "Wellenmechanik und halbzählige Quantisierung". Zeitschrift der Physik 39: 828–840.
- Brillouin, Léon (1926). "La mécanique ondulatoire de Schrödinger: une méthode générale de resolution par approximations successives". Comptes Rendus de l'Academie des Sciences 183: 24–26.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
VKB metodu Ventzel Kramers Brilluen Kvant mexanikasinda kvaziklassik yaxinlasmadir Bu metod ve arasinda elaqe qurur bele ki dalga funksiyasi klassik tesir vasitesile ifade olunur Bu metod 1926 ci ilde bir birinden asili olmadan uc fizik Q Ventzel H Kramers ve L Brilluenin terefinden inkisaf etdirildiyine gore VKB metodu adini almisdir Sredinger tenliyini yazaq ℏ22md2psdx2 U x ps Eps displaystyle frac hbar 2 2m frac d 2 psi dx 2 U x psi E psi Burada U displaystyle U potensialinin x 0 displaystyle x 0 noqtesinde minimumunun oldugu ve bu noqteden uzaqlasdiqca monoton artdigi nezerde tutulur Bele potensialda E displaystyle E enerjisine malik klassik zerrecik maddi noqte U x E displaystyle U x E tenliyinin helleri olan a displaystyle a ve b displaystyle b noqteleri arasinda periodik reqs edecek Yeni deyisenler daxil edek k x 2mℏ2 E U x displaystyle k x sqrt frac 2m hbar 2 E U x ve Sredinger tenliyini yeniden yazaq d2psdx2 k2 x ps 0 displaystyle frac d 2 psi dx 2 k 2 x psi 0 Dalga funksiyasini asagidaki sekilde gosterek ps x A x exp iℏS x displaystyle psi x A x exp frac i hbar S x burada amplitud A displaystyle A ve eksponentin quvveti S displaystyle S heqiqi nezerde tutulurlar Sonuncu ifadeni Sredinger tenliyinde nezere alsaq asagidaki alariq A S 2 Ap2 ℏ2A displaystyle A S 2 Ap 2 hbar 2 A S A 2S A 0 displaystyle S A 2S A 0 burada p x ℏk x displaystyle p x hbar k x lokal impulsdur Alinmis tenlikler Sredinger tenliyine tam ekvivalentdirler Kvaziklassik yaxinlasmada ℏ2A displaystyle hbar 2 A heddi kicik oldugu ucun atila biler bu yazinlasmasiz qeyri xetti Rikkati tenliyi deqiq hell olunmur Bu halda alinan ifadeleri inteqrallamaq olur S x x0xp x dx displaystyle S x int limits x 0 x p x dx A ps0 p x displaystyle A frac psi 0 sqrt p x burada S x displaystyle S x klassik tesire uygun gelir Neticede kvaziklassik tapmis oluruq ps x ps0 p x exp iℏ x0xp x dx displaystyle psi x frac psi 0 sqrt p x exp frac i hbar int limits x 0 x p x dx Tesvir olunan bu metod VKB metodu adlanir Xarici kecidler 1 olu kecid S C Miller Jr and R H Good Jr A WKB Type Approximation to the Schrodinger Equation Phys Rev 91 174 179 1953 2 olu kecid Carl M Bender G S Guralnik Martin L Silverstein WKB approximation for quantum theory on a lattice Phys Rev D 20 2583 2591 1979 3 olu kecid Abraham Klein and H Arthur Weldon Equations of motion variational principles and WKB approximations in quantum mechanics and quantum field theory Bound states Phys Rev D 17 1009 1030 1977 4 olu kecid Gua Xiao Yan and Sun Jian Qiang Notes on Application of WKB Method Commun Theor Phys 50 864 866 2008 IstinadlarWentzel Gregor 1926 Eine Verallgemeinerung der Quantenbedingungen fur die Zwecke der Wellenmechanik Zeitschrift der Physik 38 518 529 Kramers Hendrik A 1926 Wellenmechanik und halbzahlige Quantisierung Zeitschrift der Physik 39 828 840 Brillouin Leon 1926 La mecanique ondulatoire de Schrodinger une methode generale de resolution par approximations successives Comptes Rendus de l Academie des Sciences 183 24 26 Fizika ile elaqedar bu meqale qaralama halindadir Meqaleni redakte ederek Vikipediyani zenginlesdirin Etdiyiniz redakteleri menbe ve istinadlarla esaslandirmagi unutmayin
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans







![{\displaystyle k(x)={\sqrt {{\frac {2m}{\hbar ^{2}}}[E-U(x)]}}}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4ek9UWXhNR0l6WlRRMk1UVmlOek16WXpsa05ERTJNVEppTW1aalpXWmhOVEEyTW1FMlltWTUuc3Zn.svg)

![{\displaystyle \psi (x)=A(x)\exp {[{\frac {i}{\hbar }}S(x)]}}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aU1EUTBOR1ZpWldZMU9HWTFNRGhsTkRFd1lXWTJZVGszWVdVeE4yVXlaRFJoWm1aak1UVTIuc3Zn.svg)