Eksponent artım

Eksponent artım — artım sürəti kəmiyyətin özü ilə mütənasib olduqda kəmiyyətdəki artım. Eksponensial qanununa tabedir. Eksponensial artım daha yavaş (kifayət qədər uzun müddət ərzində) xətti və ya güc asılılıqları ilə ziddiyyət təşkil edir. Bərabər fasilələrlə ayrı-ayrı tərif sahəsi olduqda, buna həndəsi artım və ya həndəsi parçalanma da deyilir (funksiyanın dəyərləri həndəsi bir irəliləyiş əmələ gətirir). Eksponensial artım modelini maltuzian artım modeli olaraq da bilinir.

Xətti (qırmızı), güc (mavi) və eksponent (yaşıl) asılılıqlar

Xüsusiyyətlər

Hər hansı bir dərəcədə böyüyən bir miqdar üçün dəyər nə qədər yüksək olarsa, o qədər sürətli böyüyür. Bu da asılı dəyişənin böyüklüyü və artım sürətinin birbaşa mütənasib olduğunu göstərir. Ancaq eyni zamanda, hiperbolikdən fərqli olaraq, üstel əyri heç vaxt sonlu bir müddətə sonsuzluğa getmir.

Nəticədə, eksponent artım, hər bir eksponent artımdan və üstəlik, hər hansı bir xətti artımdan daha sürətli olur.

Riyazi yazısı

Eksponent artım diferensial tənliklə təsvir olunur:

${\displaystyle {\frac {dx}{dt}}=kx}$

Diferensial tənliyin həlli — eksponent funksiyadır (${\displaystyle a=1}$ və ${\displaystyle k=1}$ eksponent olur):

${\displaystyle x=ae^{kt}}$

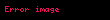
Nümunələri

Eksponensial artımın nümunə olaraq resurs məhdudiyyətlərindən əvvəl koloniyada bakteriya sayında artım ola bilər. Qarışıq faiz, eksponent artımın başqa bir nümunəsidir.

Xarici keçidlər

• Eksponent artım