Yakobi üsulu — rəqəmsal xətti cəbrdə diaqonal dominant xətti bərabərliklərin həllinin tapılması alqoritmi. Hər bir diaqonal element həll edilir və təxmini dəyər daxil edilir. Proses həllə yaxınlaşana kimi davam etdirilir. Bu üsula adı verilib.
Təsviri
Fərz edək ki,
n dərəcəli xətti bərabərliklərdir, burada:

Sonra A matrisi diaqonal D komponentinə və onun qalığı R matrisinə bölünür:
Bunun həlli təkrarlanmaqla belə tapılır
burada 

xi(k+1) hesablanması x(k)-də özündən başqa hər bir elementin olmasını tələb edir.
Nümunə
Xətti bərabərlik sistemi 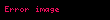
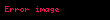
Biz 
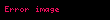







biz 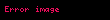
Daha sonra 
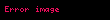



Təkrarlamanın nəticələri belədir
Bu proses yığılmaya kimi (yəni 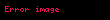
Xarici keçidlər
- Black, Noel; Moore, Shirley; and Weisstein, Eric W. Jacobi method (ing.) Wolfram saytında.
- Jacobi Method from www.math-linux.com
- Numerical matrix inversion
İstinadlar
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Yakobi usulu reqemsal xetti cebrde diaqonal dominant xetti beraberliklerin hellinin tapilmasi alqoritmi Her bir diaqonal element hell edilir ve texmini deyer daxil edilir Proses helle yaxinlasana kimi davam etdirilir Bu usula adi verilib TesviriFerz edek ki Ax b displaystyle A mathbf x mathbf b n dereceli xetti beraberliklerdir burada A a11a12 a1na21a22 a2n an1an2 ann x x1x2 xn b b1b2 bn displaystyle A begin bmatrix a 11 amp a 12 amp cdots amp a 1n a 21 amp a 22 amp cdots amp a 2n vdots amp vdots amp ddots amp vdots a n1 amp a n2 amp cdots amp a nn end bmatrix qquad mathbf x begin bmatrix x 1 x 2 vdots x n end bmatrix qquad mathbf b begin bmatrix b 1 b 2 vdots b n end bmatrix Sonra A matrisi diaqonal D komponentine ve onun qaligi R matrisine bolunur A D RwhereD a110 00a22 0 00 ann and R 0a12 a1na210 a2n an1an2 0 displaystyle A D R qquad text where qquad D begin bmatrix a 11 amp 0 amp cdots amp 0 0 amp a 22 amp cdots amp 0 vdots amp vdots amp ddots amp vdots 0 amp 0 amp cdots amp a nn end bmatrix text and R begin bmatrix 0 amp a 12 amp cdots amp a 1n a 21 amp 0 amp cdots amp a 2n vdots amp vdots amp ddots amp vdots a n1 amp a n2 amp cdots amp 0 end bmatrix Bunun helli tekrarlanmaqla bele tapilir x k 1 D 1 b Rx k displaystyle mathbf x k 1 D 1 mathbf b R mathbf x k burada x k displaystyle mathbf x k x displaystyle mathbf x nin k dereceli approksimasiyasi yaxud tekrarlanmasi ve x k 1 displaystyle mathbf x k 1 x displaystyle mathbf x nin novbeti yaxud k 1 dereceli tekrarlanmasidir Element esasli formula belece asagidaki kimidir xi k 1 1aii bi j iaijxj k i 1 2 n displaystyle x i k 1 frac 1 a ii left b i sum j neq i a ij x j k right quad i 1 2 ldots n xi k 1 hesablanmasi x k de ozunden basqa her bir elementin olmasini teleb edir NumuneXetti beraberlik sistemi Ax b displaystyle Ax b formasinda ve onun ilkin ferz edilen helli x 0 displaystyle x 0 verilib A 2157 b 1113 andx 0 11 displaystyle A begin bmatrix 2 amp 1 5 amp 7 end bmatrix b begin bmatrix 11 13 end bmatrix quad text and quad x 0 begin bmatrix 1 1 end bmatrix Biz x displaystyle x hesablamaq ucun yuxarida verilen x k 1 D 1 b Rx k displaystyle x k 1 D 1 b Rx k beraberliyinden istifade edirik Evvelce biz beraberliyi daha rahat olan D 1 b Rx k Tx k C displaystyle D 1 b Rx k Tx k C formasinda yaziriq burada T D 1R displaystyle T D 1 R ve C D 1b displaystyle C D 1 b Nezere alin ki R L U displaystyle R L U burada L displaystyle L ve U displaystyle U A displaystyle A matrisinin asagi ve yuxari hisseleridir Verilen deyerlere esasen D 1 1 2001 7 L 0050 andU 0100 displaystyle D 1 begin bmatrix 1 2 amp 0 0 amp 1 7 end bmatrix L begin bmatrix 0 amp 0 5 amp 0 end bmatrix quad text and quad U begin bmatrix 0 amp 1 0 amp 0 end bmatrix biz T D 1 L U displaystyle T D 1 L U tapiriq T 1 2001 7 00 50 0 100 0 1 2 5 70 displaystyle T begin bmatrix 1 2 amp 0 0 amp 1 7 end bmatrix left begin bmatrix 0 amp 0 5 amp 0 end bmatrix begin bmatrix 0 amp 1 0 amp 0 end bmatrix right begin bmatrix 0 amp 1 2 5 7 amp 0 end bmatrix Daha sonra C displaystyle C tapilir C 1 2001 7 1113 11 213 7 displaystyle C begin bmatrix 1 2 amp 0 0 amp 1 7 end bmatrix begin bmatrix 11 13 end bmatrix begin bmatrix 11 2 13 7 end bmatrix T displaystyle T ve C displaystyle C hesablandiqdan sonra biz x displaystyle x i x 1 Tx 0 C displaystyle x 1 Tx 0 C kimi hesablayiriq x 1 0 1 2 5 70 11 11 213 7 5 08 7 51 143 displaystyle x 1 begin bmatrix 0 amp 1 2 5 7 amp 0 end bmatrix begin bmatrix 1 1 end bmatrix begin bmatrix 11 2 13 7 end bmatrix begin bmatrix 5 0 8 7 end bmatrix approx begin bmatrix 5 1 143 end bmatrix Tekrarlamanin neticeleri beledir x 2 0 1 2 5 70 5 08 7 11 213 7 69 14 12 7 4 929 1 714 displaystyle x 2 begin bmatrix 0 amp 1 2 5 7 amp 0 end bmatrix begin bmatrix 5 0 8 7 end bmatrix begin bmatrix 11 2 13 7 end bmatrix begin bmatrix 69 14 12 7 end bmatrix approx begin bmatrix 4 929 1 714 end bmatrix Bu proses yigilmaya kimi yeni Ax n b displaystyle Ax n b kicik olana qeder davam etdirilir 25 tekrarlamadan sonra hell beledir x 7 111 3 222 displaystyle x begin bmatrix 7 111 3 222 end bmatrix Xarici kecidlerBlack Noel Moore Shirley and Weisstein Eric W Jacobi method ing Wolfram saytinda Jacobi Method from www math linux com Numerical matrix inversionIstinadlar
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State