Təcil

Təcil — sürət dəyişməsinin bu dəyişmənin baş verdiyi zaman fəsiləsinə nisbətinə bərabər olan fiziki kəmiyyət . Cismin təcillənməsi Nyutonun ikinci qanununda göstərildiyi kimi cismə təsir edən qüvvələrin əvəzləyicisinin hesabına baş verir. Beynəlxalq vahidlər sistemində (BS) təcilin vahidi metr bölünsün saniyə kvadratıdır (${\displaystyle m \over san^{2}}$). Təcil vektorial kəmiyyətdir (yəni həm qiyməti həm də istiqaməti ilə müəyyən olunur) və paraleloqram qanununa görə cəmlənir. Bir vektor kimi hesablanan əvəzləyici qüvvə cismin kütləsi (skalyar kəmiyyətdir) ilə onun təcilinin hasilinə bərabərdir.

Təcil
a
Ölçü vahidi
BS
Qeyd
və sürtünmə qüvvəsi olmadıqda düşən top sürətini artırmağa davam edəcəkdir.
Vikianbarda əlaqəli mediafayllar

Misal üçün bir avtomobil hərəkətsiz haldan (başlanğıc sürəti 0 olan haldan) düz xətt boyunca sürətini artıraraq hərəkət edərkən, təcilin istiqaməti hərəkət istiqamətində yönəlir. Əgər avtomobil dönərsə, təcil istiqamətini dəyişərək yeni istiqamət alır. Bu misalda avtomobildəki sərnişinlərin müşahidə etdiyi onları oturacağa doğru itələyən və ya basan qüvvəni maşının təcili və ya xətti təcil adlanır. Avtomobil istiqamətini dəyişərkən avtomobildəki sərnişinlər onları yan tərəfə doğru itələyən qüvvələrin yarandığını müşahidə edəcəklər belə təcil qeyri xətti təcil adlanır. Əgər avtomobil sürətini azaldarsa, bu zaman təcil avtomobilin hərəkət istiqamətinin əksinə yönəlir və buna bəzən yavaşıma deyilir.Yavaşıma zamanı sərnişinlər onları önə doğru itələyən qüvvənin meydana gəldiyini müşahidə edirlər.Riyazi olaraq yavaşımanın ayrıca bir düsturu yoxdur,hər ikisidə surət dəyişməsidir. Bu təcillərin hər biri (xətti, qeyri-xətti yavaşıyan, yeyinləşən) sərnişinlər tərəfindən onlarin sürətləri (sürətin qiymət və istiqaməti) avtomobilin sürəti ilə eyni olana qədər hiss edilir.

Tərifi və xassələri

Klassik hissəciyin kinematik kəmiyyətləri: kütlə m, məsafə r, sürət v, təcil a.

Orta təcil

Təcil sürətin dəyişmə miqdarıdır.Trayektoriyanın hər hansı bir nöqtəsində təcilin qiyməti həmən nöqtədə sürətin həm qiymətinin həmdə istiqamətinin dəyişmə yeyinliyi ilə xarakterizə olunur. t anındakı həqiqi təcil zaman intervalının limitlənməsi ilə tapılır. Δt → 0, Δv/Δt

Əgər cismin orta təcili sürət dəyişməsinin (delta v) həmin dəyişmənin baş verdiyi zaman fasiləsinə (delta t) nisbətinin təcilinə bərabərdir. Riyazi ifadəsi:

${\displaystyle \mathbf {\bar {a}} ={\frac {\Delta \mathbf {v} }{\Delta t}}.}$

Ani təcil

Aşağıdan yuxarıya doğru :təcil funksiyasi a(t) sürət funksiyası təcilin inteqralıdır v(t) və sürətin inteqralı isə yerdəyişmənin funksiyasıdır s(t)

Ani təcil orta təcilin sonsuz kiçik zaman intervalındakı limitinə bərabərdir.Hesablamalarda ani təcili sürət vektorunun zamana görə birinci tərtib törəməsi kimi götürürlər,

${\displaystyle \mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}}$

(Burada və ya başqa yerdə əgər hərəkət düzxətlidirsə tənliklərdə vektorial kəmiyyətləri skaliarla əvəzetmək olar.)

təcil funksiyasınınn integralı a(t) sürət funksiyasına bərabərdir v(t); buda sürətə görə təcilin zamandan asılılıq qrafikində (a vs. t) əyrinin altinda qalan sahəyə bərabərdir.

${\displaystyle \mathbf {v} =\int \mathbf {a} \ dt}$

Təcil sürətin ,v, zamana,t, görə birinci tərtib törəməsi ilə müəyyən olunur və sürət isə koordinatın,x, zamana görə birinci tərtib törəməsi ilə müəyyən olunur və buna görə də təcil koordinatın zamana görə ikinci tərtib törəməsi hesab olunur

${\displaystyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}}$

Kəmiyyətlər

 Təcil sürət dimenzionu bölünsün zaman (L/T) dimenzionuna bərabərdir və s. L.T⁻². Beynəlxalq vahidlər sistemində təcil vahidi olaraq metr bölünsün saniyə kvadratı qəbul edilib (m s⁻²); və ya"metr böl saniyə böl saniyə" , hər saniyədə sürətini bir metr böl saniyə dəyişməsinə təcil deyilir.

Digər formaları

Çevrə boyunca hərəkət edən cismin hərəkəti- peykin yer kürəsinin ətrafında hərəkəti — baxmayaraqki sürətin qiyməti sabit qala bilər lakin istiqamətin dəyişməsinə görə belə hərəkət təcilli hərəkətdir.Belə hərəkət zamanı yaranan təcilə mərkəzə qaçma təcili deyilir.

Tam təcil ,sərbəst düşən cismin tam təcilini hesablamaq üçün istifadə olunan cihaz akselerometr adlanır.

klassik mexanikada sabit kütləli cismə təsir edən qüvənin əvəzləyicisi onun təcili və kütləsi ilə düz mütənasibdir (Nyutonun ikinci qanunu):

${\displaystyle \mathbf {F} =m\mathbf {a} \quad \to \quad \mathbf {a} =\mathbf {F} /m}$

Təcil, vahid zamanda cismin sürətinin dəyişmə yeyinliyidir. Cismin təcilllnməsi Nyutonun ikinci qanunundada gostərildiyi kimi cismə təsir edən qüvvələrin əvəzləyicisinin hesabina baş verir. Beynəlxalq vahidlər sistemində (BS) təcilin vahidi metr bölünsünsaniyə kvadratıdır (m s⁻²). Təcil vektorial kəmiyyətdir (yəni həm qiyməti həmdə istiqaməti ilə müəyyən olunur) və paralelogram qanununa görə cəmlənir.Bir vektor kimi hesablanan əvəzləyici qüvvə cismin kutləsi(skalyar kəmiyyətdir) ilə onun təcilinin hasilinə bərabərdir

Sürət və təcili göstərilmiş riyazi rəqqas.Bu tangensial və normal təcili təcrübə edir.

Əyrixətli hərəkətdə təcilin komponentləri. Tangensial komponent a_t tangensial təcil əyriyə toxunan istiqametində yönəlir , və əyri boyunca yönəlib sürət vektorunu göstərir (və ya əks istiqamətdə). Normal təcilin komponenti (və ya cevrəboyunca hərəkətdə mərkəzə qaçma təcili) a_c sürət vektorunun dəyişməsinə görə trayektoriyanın normalıdır və əyrinin mərkəzinə doğru yönəlir, 

əyrixətli hərəkətdə cismin sürətinin zamandan aslılıq funksiyası aşağıdakı şəkildə yazılır:

${\displaystyle \mathbf {v} (t)=v(t){\frac {\mathbf {v} (t)}{v(t)}}=v(t)\mathbf {u} _{\mathrm {t} }(t),}$

 v(t) trayektoriya boyunca hərəkət edən cismin sürətinə bərabərdir və

${\displaystyle \mathbf {u} _{\mathrm {t} }={\frac {\mathbf {v} (t)}{v(t)}}\ ,}$

${\displaystyle \mathbf {u} _{\mathrm {t} }={\frac {\mathbf {v} (t)}{v(t)}}\ ,}$

${\displaystyle \mathbf {u} _{\mathrm {t} }={\frac {\mathbf {v} (t)}{v(t)}}\ ,}$

verilmiş zaman anında hərəkət istiqamətinə toxunan yönəlmiş vahid tangensial vektordur. Nəzərə almaq lazımdırki əyrixətli hərəkət edən cismin təcilini hər iki halda sürətin qiymətinin v(t) və istiqamətinin u_t, dəyişməsinə görə differensialın zəncir qaydasından istifadə edərək asağıdakı şəkildə yazmaq olar :

${\displaystyle {\begin{alignedat}{3}\mathbf {a} &={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}\\&={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }+v(t){\frac {d\mathbf {u} _{\mathrm {t} }}{dt}}\\&={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }+{\frac {v^{2}}{r}}\mathbf {u} _{\mathrm {n} }\ ,\\\end{alignedat}}}$

${\displaystyle \mathbf {\bar {a}} ={\frac {\Delta \mathbf {v} }{\Delta t}}.}$

Hendesi analizin üç ölçülü əyriləri hansıki izah edir tangensial. normal ve binormalı. Frenet–Serret düsturunda təsvir olunub.

Xüsusi hallar

${\displaystyle \mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}}$

Bircins sabit təcil bərabər zaman fasiləsində sürətini eyni qədər dəyişən cismin hərəkətidir. Bircins təcilə ən sadə misal bircins qravitasiya sahəsində sərbəst düşən cismin hərəkətidir.Sərbəst düşən cismin hərəkəti müqavimətsiz mühitdə yalnız qravitasiya sahəsinin gücündən g (və ya sərbəstdüşmə təcilindən) asılıdır. Nyutonun ikinci qanununa görə cismə təsir edən qüvvə:

${\displaystyle \mathbf {F} =m\mathbf {g} }$

sadə analitik xassələrə görə yerdəyişmə ,başlanğıc və son sürətin təcil ilə əlaqəli aşağıdakı düsturları mövcuddur:

${\displaystyle \mathbf {s} (t)=\mathbf {s} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}=\mathbf {s} _{0}+{\frac {\mathbf {v} _{0}+\mathbf {v} (t)}{2}}t}$

${\displaystyle \mathbf {v} (t)=\mathbf {v} _{0}+\mathbf {a} t}$

${\displaystyle {v^{2}}(t)={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}]}$

hansıki

• ${\displaystyle t}$ sərf olunan zaman,
• ${\displaystyle \mathbf {s} _{0}}$ balanğıc yerdəyişmə əvvəl olduğu yerdən,
• ${\displaystyle \mathbf {s} (t)}$ son yerdəyişmə ${\displaystyle t}$,
• ${\displaystyle \mathbf {v} _{0}}$ başlanğıc sürət,
• ${\displaystyle \mathbf {v} (t)}$ son sürət ${\displaystyle t}$, və 
• ${\displaystyle \mathbf {a} }$ bircins təcil.

Xüsusilə hərəkət iki ortoqonal hissəyə ayrılır birincisi sabit surətli olub ikincisi isə yuxarıdakı tənliklərdən birinə gorə dəyişir. Galileo göstərdiki,bu parabolik hərəkətdir məselen bir mərminin yer səthinə yaxın bir vakkum içində trayektoriyasi

Dairəvi hərəkət

Bircins dairəvi hərəkət, bu çevrə üzrə bərabərsürətli hərəkətdir. Belə hərəkət edən cismin sürətinin ədədi qiyməti sabit istiqaməti isə zaman keçdikcə dəyişir.Sürətin istiqaməti dəyişdiyindən çevrə üzrə hərəkət təcilli hərəkətdir.Çevrənin istənilən nöqtəsindəki təcil vektoru sürət vektoruna perpendikulyar olur və çevrə mərkəzinə doğru yönəlir.Radius boyunca çevrənin mərkəzinə doğru yönəlmiş təcilə mərkəzəqaçma təcili deyilir. Mərkəzəqaçma təcilinin modulu aşağıdakı kimi ifadə olunur :

${\displaystyle {\textrm {a}}={{v^{2}} \over {r}}}$

 ${\displaystyle v}$ Çevrə boyunca hərəkət edən cismin xətti sürətidir. Buna ekvivalent olaraq çevrə boyunca hərəkət edən cismin təcilini bucaq sürəti adlanan kəmiyyətlədə təyin edirlər 

${\displaystyle \mathbf {a} ={-\omega ^{2}}\mathbf {r} }$

 ${\displaystyle \mathbf {r} }$ Çevrənin merkəzindən yönələn radius vektordur və qiyməti radiusun uzunluğuna bərabərdir.Mənfi işarəsi təcilin çevrənin mərkəzinə doğru yönəldiyini (radius vektorun əksinə) göstərir.

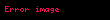
Bircins dairəvi hərəkətdə təcil və əvəzləyici qüvvə çevrənin mərkəzinə doğru yönəlir ; Bu mərkəzidir. Halbuki, mərkəzdən qaçma qüvvəsi adlanan bu qüvvə cismdən xaricə doğru yönələn həqiqi psevdo qüvvədir cismin hərəkət trayektoriyası düz xətt deyilsə belə hərəkət əyrixətli hərəkət adlanır. Əyrixətli hərəkətdə cismin hərəkət istiqaməti daima dəyişdiyindən hərəkət təcilli hərəkətdir. Əyrixətli trayektoriyaya çəkilmiş toxunan istiqamətində yönəlir. Trayektoriyaya toxunan istiqamətdə yönəlmiş və sürətin modulca dəyişməsini xarakterizə edən təcil toxunan və ya tangensial təcil adlanır.Toxunana perpendikulyar olan və sürətin istiqametcə dəyişməsini xarakterizə edən təcil normal və ya mərkəzəqaçma təcili adlanır.

${\displaystyle a=r\alpha .}$

Tangensial təcil radius vektora perpendikulyar yönəlir və bucaq təcili adlanır(${\displaystyle \alpha }$).

Nisbilik nəzəriyyəsi ilə əlaqəsi

xüsusi nisbilik nəzəriyyəsi

Xüsusi nisbilik nəzəriyyəsi — differensial qiymət qazanan təcil vektorlarının nisbilik nəzəriyyəsinə əsasən izah olunaraq ifadə olunmasıdır .

Orta məktəb üçün sadə düstur

${\displaystyle {\vec {a}}={\frac {{\vec {v}}-{\vec {v}}_{0}}{t}}}$
a-təcil,v-son sürət,v₀-başlanğıc sürət,t-sürət dəyişməsinə sərf olunan zamandır.v₀=0 olanda düstur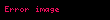
${\displaystyle {\vec {a}}={\frac {\vec {v}}{t}}}$ olar.

Bircins təcil

Xüsusi nisbilik nəzəriyyəsi vakkumda hərəkət edən cisimlərin sürətlərinin işıq sürətinə yaxın sürətlərdə hərəkətinin digər cisimlərə nəzərən öyrənilməsidir. Nyutonun mexanikası işıq sürətindən çox-çox kiçik sürətlə hərəkət edən cisimlər üçün doğrudur. Cisimlərin sürətləri işiq sürətinə qədər artdıqca təcil artıq klassik düsturlarla hesablana bilmir.

Cisimlərin sürəti işıq sürətinə yaxınlaşdıqca verilmiş qüvvənin yaratdığı təcil azalır,və işıq sürətinə yaxınlaşdıqca sonsuz kiçilməyə başlayır; müəyyən kütləyə malik cisim işıq sürətinə assimptotik yaxınlaşır lakin onu heç vaxt keçə bilmir.

Ümumi nisbilik

Ümumi nisbilik nəzəriyyəsi təcillə hərəkət edən (qeyri-ətalət) hesablama sistemlərində kainatda baş verən proseslerin məkan və zaman xassələrini öyrənir. Nyutonun ümumdünya cazibə qanunu zəif sahələr üçün doğrudur. Ümumi nisbilik nəzəriyyəsi isə sıxlığı çox böyük olan neytron ulduzlarının yaxınlığında güclü qravitasiya sahəsi yaranır. Belə ulduzların ətrafında fəzanın əyilməsi baş verir və zamanın gedişi ləngiyir. Deməli güclü qravitasiya sahəsi fəza və zamanın həndəsi xassələrini dəyişdirir.

İstinadlar

1. Larry C. Andrews; Ronald L. Phillips. Mathematical Techniques for Engineers and Scientists. SPIE Press. 2003. səh. 164. ISBN . 2021-03-22 tarixində . İstifadə tarixi: 2016-12-26.
2. Ch V Ramana Murthy; NC Srinivas. Applied Mathematics. New Delhi: S. Chand & Co. 2001. səh. 337. ISBN . 2021-04-28 tarixində . İstifadə tarixi: 2016-12-26.
3. Keith Johnson. Physics for you: revised national curriculum edition for GCSE (4th). Nelson Thornes. 2001. səh. 135. ISBN . 2021-10-11 tarixində . İstifadə tarixi: 2016-12-26.
4. David C. Cassidy; Gerald James Holton; F. James Rutherford. Understanding physics. Birkhäuser. 2002. səh. 146. ISBN . 2021-03-22 tarixində . İstifadə tarixi: 2016-12-26.
5. Brian Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, page 67.

• Acceleration Calculator Simple acceleration unit converter
• Measurespeed.com — Acceleration Calculator Based on starting & ending speed and time elapsed.