Yalnız bir binar cəbri əməlin təyin edildiyi cəbri strukturaya qruppoid deyilir; deməli, qruppoid üçün əməlinə nəzərən aşağıdakı şərt ödənməlidir:
Qruppoiddə bu şərtdən əlavə assosiativlik xassəsinə aid
aksiomu da ödənərsə, buna yarımqrup deyilir. Deməli, yarımqrup elə cəbri strukturdur ki, orada iki şərt ödənir: 1) əməlinin təyin edilməsi; 2) bu əməlin assosiativlik xassəsinə malik olması. Cəbrə aid ədəbiyyatda bəzən yarımqrup əmələ gətirən çoxluğunu məhz assosiativ qruppoid adlandırırlar. Xüsusi şərtləşmə olmadıqda qruppoiddə təyin edilən kompozisiyası adətən vurma əməli kimi qəbul edilir və bu kimi işarə edilir. Lakin bəzən təyin edilən cəbri əməli toplama kimi də qəbul edilir. Vurma əməlinə nəzərən qruppoidə multiplikativ, toplama əməlinə nəzərən qruppoidə isə additiv qruppoid deyirlər. Sonrakı mühakimələrimizi adətən multiplikativ qruppoid, yarımqruplar üzərində aparmağı şərtləşək. Əgər qruppoiddə və yarımqrupda əlavə bir aksiom — vurmada kommutativlik xassəsi ödənərsə, onda uyğun olaraq bunları kommutativ qruppoid və kommutativ yarımqrup adlandırırlar. Təriflərdən aydın olur ki, istər qruppoiddə, istərsə də yarımqrupda neytral elementin olması vacib sayılmır. Yarımqrupda neytral element olarsa, buna monoid deyilir. Deməli, monoid elə cəbri strukturdur ki, orada aşağıdakı şərtlər ödənir:
1)
2)
3) .
əməlinin vurma və toplama olmasına uyğun olaraq monoidi uyğun olaraq multiplikativ və additiv adlandırmaq olar. çoxluğunun vurma və toplama cəbri əməllərinə nəzərən əmələ gətirdiyi multiplikativ və additiv monoidləri uyğun olaraq kimi işarə edə bilərik. Təyin edildiyi əməl kommutativlik xassəsinə malikdirsə, belə monoidə kommutativ monoid deyirlər. Həqiqi ədədlər çoxluğu -i yada salaq. həqiqi ədələr çoxluğu ayrılıqda həm toplama, həm də vurma əməllərinə görə kommutativ qruppoiddir. Çünki, bu çoxluqda üçün və , yəni -də toplama və vurma əməlləri təyin edilib, həm də . Bu çoxluqda təyin edilən əməllər assosiativlik xassəsinə malik olduğu üçün ayrılıqda hər iki əmələ nəzərən yarımqrupdur. Burada neytral (vahid) element olduğu üçün bu həm də monoiddir, özü də kommutativdir. Digər bir misala baxaq, natural ədədinə bölünən tam ədədlər çoxluğunu götürək: Bu çoxluq toplamaya nəzərən kommutativ monoid əmələ gətirir, vurmaya nəzərən isə vahidi olmayan yarımqrupdur(burada ). Qruppoiddə onun ixtiyari elementi üçün şərti ödənərsə, buna idempotent qruppoid deyilir. Əgər qruppoiddə vahid element varsa o, yeganədir. Qruppoid, yarımqrup, monoid kimi cəbri strukturlar bir çox ümumi və spesifik xassələrə malikdirlər. Bunların öyrənilməsi bir cox cəhətdən qrup anlayışının öyrənilməsini xatırladır, burada geniş analogiya vardır.
Ədəbiyyat
- Maarif Əkbərov "Cəbr və Ədədlər nəzəriyyəsi"
- , Линейная алгебра, М.: Наука — Физматлит, 1999.
- Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2000.
- Введение в алгебру. Часть 1. Основы алгебры: Учебник для вузов. М.: Физматлит, 2004.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Yalniz bir binar cebri emelin teyin edildiyi cebri strukturaya qruppoid deyilir demeli qruppoid ucun displaystyle otimes emeline nezeren asagidaki sert odenmelidir a b M displaystyle forall a b in M c M displaystyle exists c in M a b c displaystyle a otimes b c Qruppoidde bu sertden elave assosiativlik xassesine aid a b c M displaystyle forall a b c in M a b c a b c displaystyle a otimes b otimes c a otimes b otimes c aksiomu da odenerse buna yarimqrup deyilir Demeli yarimqrup ele cebri strukturdur ki orada iki sert odenir 1 displaystyle otimes emelinin teyin edilmesi 2 bu emelin assosiativlik xassesine malik olmasi Cebre aid edebiyyatda bezen yarimqrup emele getiren M displaystyle M coxlugunu mehz assosiativ qruppoid adlandirirlar Xususi sertlesme olmadiqda qruppoidde teyin edilen displaystyle otimes kompozisiyasi adeten vurma emeli kimi qebul edilir ve bu lt G gt displaystyle lt Gamma cdot gt kimi isare edilir Lakin bezen teyin edilen displaystyle otimes cebri emeli toplama kimi de qebul edilir Vurma emeline nezeren qruppoide multiplikativ toplama emeline nezeren qruppoide ise additiv qruppoid deyirler Sonraki muhakimelerimizi adeten multiplikativ qruppoid yarimqruplar uzerinde aparmagi sertlesek Eger qruppoidde ve yarimqrupda elave bir aksiom vurmada kommutativlik xassesi ab ba displaystyle ab ba odenerse onda uygun olaraq bunlari kommutativ qruppoid ve kommutativ yarimqrup adlandirirlar Teriflerden aydin olur ki ister qruppoidde isterse de yarimqrupda neytral elementin olmasi vacib sayilmir Yarimqrupda neytral element olarsa buna monoid deyilir Demeli monoid ele cebri strukturdur ki orada asagidaki sertler odenir 1 a b M displaystyle forall a b in M c M displaystyle exists c in M a b c displaystyle a otimes b c 2 a b c M displaystyle forall a b c in M a b c a b c displaystyle a otimes b otimes c a otimes b otimes c 3 e M displaystyle exists e in M a M displaystyle forall a in M e a a e a displaystyle e otimes a a otimes e a displaystyle otimes emelinin vurma ve toplama olmasina uygun olaraq monoidi uygun olaraq multiplikativ ve additiv adlandirmaq olar M displaystyle M coxlugunun vurma ve toplama cebri emellerine nezeren emele getirdiyi multiplikativ ve additiv monoidleri uygun olaraq lt M e gt lt M 8 gt displaystyle lt M cdot e gt lt M theta gt kimi isare ede bilerik Teyin edildiyi emel kommutativlik xassesine malikdirse bele monoide kommutativ monoid deyirler Heqiqi ededler coxlugu R displaystyle R i yada salaq R displaystyle R heqiqi edeler coxlugu ayriliqda hem toplama hem de vurma emellerine gore kommutativ qruppoiddir Cunki bu coxluqda a b R displaystyle forall a b in R ucun a b R displaystyle a b R ve a b R displaystyle a cdot b R yeni R displaystyle R de toplama ve vurma emelleri teyin edilib hem de a b b a ab ba displaystyle a b b a ab ba Bu coxluqda teyin edilen emeller assosiativlik xassesine malik oldugu ucun ayriliqda her iki emele nezeren yarimqrupdur Burada neytral vahid element oldugu ucun bu hem de monoiddir ozu de kommutativdir Diger bir misala baxaq n displaystyle n natural ededine bolunen tam ededler coxlugunu goturek nZ nm m Z displaystyle nZ nm mid m in Z Bu coxluq toplamaya nezeren kommutativ monoid emele getirir vurmaya nezeren ise vahidi olmayan yarimqrupdur burada n gt 1 displaystyle n gt 1 Qruppoidde onun ixtiyari elementi ucun serti odenerse buna idempotent qruppoid deyilir Eger qruppoidde vahid element varsa o yeganedir Qruppoid yarimqrup monoid kimi cebri strukturlar bir cox umumi ve spesifik xasselere malikdirler Bunlarin oyrenilmesi bir cox cehetden qrup anlayisinin oyrenilmesini xatirladir burada genis analogiya vardir Edebiyyat Maarif Ekberov Cebr ve Ededler nezeriyyesi Linejnaya algebra M Nauka Fizmatlit 1999 Kurs analiticheskoj geometrii i linejnoj algebry M Fizmatlit 2000 Vvedenie v algebru Chast 1 Osnovy algebry Uchebnik dlya vuzov M Fizmatlit 2004
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans





![{\displaystyle [a\otimes (b\otimes c)=(a\otimes b)\otimes c]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4eU5HVmxNV1k1TURWaVptVTVaR1EwTjJJMU1qSTRPR05qWXpSaE16ZGhZMkk1TUdJeFlUVTQuc3Zn.svg)
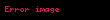



![{\displaystyle [a\otimes (b\otimes c)=(a\otimes b)\otimes c],}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aE5XSTFPVGxtTXpSaE9HRXpPREkyWm1FMk1USXlaR0ppTnpSaE5UVmhPVGt6WlRjNU5XRXguc3Zn.svg)











