Bu məqalədə heç bir məlumatın mənbəsi . |
Qeyri-səlis çoxluq (və ya əlamətsiz çoxluq) anlayışı, çoxluq anlayışının element olmanın qiymətləndirilməsinə söykənən ümumiləşdirmədir. Qeyri-səlis çoxluq əlamətsiz məntiqin təbii bir ümumiləşməsi olaraq 1965-ci ildə Lütfi Zadə tərəfindən isbat edilmişdir. Bir obyekt bir çoxluğun ya elementi ya da elementi olmadığı halda, bir qeyri-səlis çoxluğun müəyyən bir nisbətdə qismən elementi ola bilər.
Təsvir

Qeyri-səlis çoxluq müxtəlif cür də göstərilə bilər ancaq çoxluğun hər nöqtə üçün 
Bir 








Əgər 






Məsələn 




Qeyri-səlis alt çoxluq























Qeyri-səlis çoxluq üzərində əməliyyatlar
Çoxluqlar üçün qəbul edilən birləşmə, kəsişmə, karteziyan vurması kimi əməliyyatların hamısı qeyri-səlis çoxluğada şamil edilir. İki bulanık kümenin birleşimi 


İki qeyri-səlis çoxluğun birləşməsi 

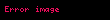

İki qeyri-səlis çoxluğun kəsişməsi isə 


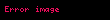
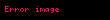


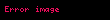
İki çoxluq üçün göstərilən bu əməliyyatlar və yerinə sırasıyla və alınaraq hər hansı sayıdakı qeyri-səlis çoxluq ailəsinə genişləndirilə bilər.
Həmçinin bax
Xarici keçidlər
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqalede hec bir melumatin menbesi gosterilmemisdir Lutfen etibarli menbeler elave etmekle meqaleni tekmillesdirmeye komek edin Qerez yaradan menbesiz hisseler muzakiresiz siline biler Qeyri selis coxluq ve ya elametsiz coxluq anlayisi coxluq anlayisinin element olmanin qiymetlendirilmesine soykenen umumilesdirmedir Qeyri selis coxluq elametsiz mentiqin tebii bir umumilesmesi olaraq 1965 ci ilde Lutfi Zade terefinden isbat edilmisdir Bir obyekt bir coxlugun ya elementi ya da elementi olmadigi halda bir qeyri selis coxlugun mueyyen bir nisbetde qismen elementi ola biler TesvirX displaystyle X sifirdan ferqli bir universal coxluq olaraq secilsin Bir A X 0 1 displaystyle A X to 0 1 funksiyasina X displaystyle X uzerinde bir qeyri selis coxluq adi verilir Qeyri selis coxluq muxtelif cur de gosterile biler ancaq coxlugun her noqte ucun 0 1 displaystyle 0 1 araliginda qapali bir qiymet almasi baximindan bu tesvirlerin hamisi bir birine beraberdir Bir x displaystyle x X displaystyle X elementi ucun A x displaystyle A x qiymetine x displaystyle x in A daki elementlik derecesi deyilir Bu qiymet kimi zaman mA x displaystyle mu A x ile de gosterilir A x 1 displaystyle A x 1 olmasi klassik coxluq anlayisinda x displaystyle x in A displaystyle A nin elementi olmasi A x 0 displaystyle A x 0 olmasi ise klassik coxluqlarda x displaystyle x in A displaystyle A nin elementi olmamasi menasina gelir Eger x displaystyle x ucun A x a displaystyle A x alpha ise x displaystyle x aA displaystyle A yazilir ve x displaystyle x in A displaystyle A qeyri selis coxlugunun a displaystyle alpha derecesinde elementi oldugu deyilir Meselen A x 0 5 displaystyle A x 0 5 yeni x displaystyle x 0 5A displaystyle A olmasi x displaystyle x in A displaystyle A nin yari yariya elementi olmasi seklinde gosterilir 1 klassik 0 klassik simvoluna qarsiliq gelir Qeyri selis alt coxluqA displaystyle A ve B displaystyle B bos olmayan bir X displaystyle X coxlugu uzerinde iki qeyri selis coxluq olsun Her x X displaystyle x in X ucun A x B x displaystyle A x leq B x olursa A B displaystyle A subseteq B ve ya A B displaystyle A leq B yazilir ve A displaystyle A nin B displaystyle B nin bir qeyri selis alt coxlugu oldugu deyilir A displaystyle A ve B displaystyle B qeyri selis coxlugun beraberliyi her x displaystyle x X displaystyle X ucun A x B x displaystyle A x B x olmasi ile gosterilir Buna gore A displaystyle A nin B displaystyle B ye beraber olmasi eyni zamanda hem A B displaystyle A subseteq B hem de B A displaystyle B subseteq A olmasi demekdir X displaystyle X uzerindeki butun qeyri selis coxlugu her x displaystyle x X displaystyle X ucun X x 1 displaystyle X x 1 ile gosterilen X displaystyle X qeyri selis alt coxlugu iken her x displaystyle x X displaystyle X ucun x 0 displaystyle varnothing x 0 ile gosterilen displaystyle varnothing qeyri selis coxlugu X displaystyle X deki butun qeyri selis coxlugun alt coxlugudur Bezen X displaystyle X ve displaystyle varnothing simvollari yerine sirasiyla 1X displaystyle 1 X ve 0X displaystyle 0 X ve ya qisaca 1 displaystyle 1 ve 0 displaystyle 0 istifade edilir Qeyri selis coxluq uzerinde emeliyyatlarCoxluqlar ucun qebul edilen birlesme kesisme karteziyan vurmasi kimi emeliyyatlarin hamisi qeyri selis coxlugada samil edilir Iki bulanik kumenin birlesimi A B displaystyle A cup B veya A B displaystyle A lor B ile gosterilir ve bu kumeye eleman olma derecesi her x displaystyle x X displaystyle X icin A B x maks A x B x displaystyle A cup B x maks A x B x olarak tanimlanir Iki qeyri selis coxlugun birlesmesi A B displaystyle A cup B ve ya A B displaystyle A lor B ile gosterilir ve bu coxluga element olma derecesi her x displaystyle x X displaystyle X ucun A B x maks A x B x displaystyle A cup B x maks A x B x olaraq gosterilir Iki qeyri selis coxlugun kesismesi ise A B displaystyle A cap B ve ya A B displaystyle A land B ile gosterilir ve bu coxluga element olma derecesi her x displaystyle x X displaystyle X ucun A B x min A x B x displaystyle A cap B x min A x B x olaraq gosterilir A displaystyle A ve B displaystyle B sirasiyla X displaystyle X ve Y displaystyle Y coxlugu uzerinde qeyri selis coxluqlar ise A B displaystyle A times B de X Y displaystyle X times Y uzerinde bir qeyri selis coxluqdur ve her x y X Y displaystyle x y in X times Y ucun A B x y min A x B y displaystyle A times B x y min A x B y seklinde gosterilir Iki coxluq ucun gosterilen bu emeliyyatlar ve yerine sirasiyla ve alinaraq her hansi sayidaki qeyri selis coxluq ailesine genislendirile biler Hemcinin baxQeyri selis mentiq CoxluqXarici kecidler
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans