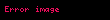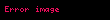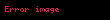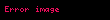Qauss üsulu — Xətti tənliklər sistemini həll etmək üçün klassik üsul. Bəzən bu üsula əmsalları yoxetmə üsulu da adlanır.
Tutaq ki, kvadrat xətti tənliklər sistemi verilmişdir
Bu sistemin həlli üçün məchulun yox edilməsi və ya Qausus üsulunun mahiyyəti aşağıdakı kimidir. Tutaq ki, . Onda sistemin birinci tənliyinin hər iki tərəfini vuraraq alınan
tənliyini sistemin ikinci tənliyindən tərəf-tərəfə çıxaq. Aldığımız tənlikdə məchulu iştirak etmir.
Sonra sistemin birinci tənliyinin hər iki tərəfini vuraraq alınan tənliyini sistemin üçüncü tənliyindən tərəf-tərəfə çıxaq. Bu mühakiməni ardıcıl tətbiq etməklə (1) sistemini
şəklində sistemə gətirmək olar. Aldığımız yeni sistemin 2-ci, 3-cü və s. tənliklərdən istifadə etməklə yuxarıda gördüyümüz üsulla məchulunuda yox etmək olar. Bu mühakiməni ardıcıl olaraq tətbiq etməklə (1) sistemini ona ekvivalent olan
tənliklər sisteminə gətirmək olar. (3) sisteminə pilləvari (və ya pilləkən şəklində) sistem deyilir. sonuncu tənlikdən məchulu tapılır, sonra yuxarı qalxaraq və bu qayda ilə davam edərək birinci tənlikdən məchulunu tapırıq. (1) sistemini Qauss üsulu ilə həll edərkən tənliklər üzərində aparılan əməlləri bəzən onların əmsallarından düzəlmiş
matrisi üzərində aparmaq daha münasib olur. Belə matris genişlənmiş matris adlanır.
Mənbə
http://brain.ilkaddimlar.com/login.html 2017-05-25 at the Wayback Machine
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Qauss usulu Xetti tenlikler sistemini hell etmek ucun klassik usul Bezen bu usula emsallari yoxetme usulu da adlanir Tutaq ki kvadrat xetti tenlikler sistemi verilmisdir a11x1 a12x2 a1nxn b1a21x1 a22x2 a2nxn b2 am1x1 am2x2 amnxn bm 1 displaystyle begin cases a 11 x 1 amp a 12 x 2 amp dots amp a 1n x n amp b 1 a 21 x 1 amp a 22 x 2 amp dots amp a 2n x n amp b 2 dots amp dots amp dots amp dots amp dots a m1 x 1 amp a m2 x 2 amp dots amp a mn x n amp b m end cases 1 Bu sistemin helli ucun mechulun yox edilmesi ve ya Qausus usulunun mahiyyeti asagidaki kimidir Tutaq ki a11 0 displaystyle a 11 neq 0 Onda sistemin birinci tenliyinin her iki terefini a21a11 displaystyle frac a 21 a 11 vuraraq alinan a21x1 a12a21a11x2 a1na21a11xn a21a11b1 displaystyle a 21 x 1 frac a 12 a 21 a 11 x 2 frac a 1n a 21 a 11 x n frac a 21 a 11 b 1 tenliyini sistemin ikinci tenliyinden teref terefe cixaq Aldigimiz tenlikde x1 displaystyle x 1 mechulu istirak etmir a22 x2 a23 x3 a2n xn b2 displaystyle a 22 x 2 a 23 x 3 a 2n x n b 2 Sonra sistemin birinci tenliyinin her iki terefini a21a11 displaystyle frac a 21 a 11 vuraraq alinan tenliyini sistemin ucuncu tenliyinden teref terefe cixaq Bu muhakimeni ardicil tetbiq etmekle 1 sistemini a11x1 a12x2 a1nxn b1a22 x2 a2n xn b2 an2 x2 ann xn bn 2 displaystyle begin cases a 11 x 1 amp a 12 x 2 amp dots amp a 1n x n amp b 1 a 22 x 2 amp dots amp a 2n x n amp b 2 amp dots amp dots amp dots a n2 x 2 amp dots amp a nn x n amp b n end cases 2 seklinde sisteme getirmek olar Aldigimiz yeni sistemin 2 ci 3 cu ve s tenliklerden istifade etmekle yuxarida gorduyumuz usulla x2 displaystyle x 2 mechulunuda yox etmek olar Bu muhakimeni ardicil olaraq tetbiq etmekle 1 sistemini ona ekvivalent olan a11x1 a12x2 a1nxn b1a22 x2 a2n xn b2 a nn n 1 xn b nn n 1 3 displaystyle begin cases a 11 x 1 amp a 12 x 2 amp dots amp a 1n x n amp b 1 a 22 x 2 amp dots amp a 2n x n amp b 2 amp dots amp dots amp dots a nn n 1 x n amp b nn n 1 end cases 3 tenlikler sistemine getirmek olar 3 sistemine pillevari ve ya pilleken seklinde sistem deyilir sonuncu tenlikden xn displaystyle x n mechulu tapilir sonra yuxari qalxaraq x n 1 displaystyle x n 1 ve bu qayda ile davam ederek birinci tenlikden x1 displaystyle x 1 mechulunu tapiriq 1 sistemini Qauss usulu ile hell ederken tenlikler uzerinde aparilan emelleri bezen onlarin emsallarindan duzelmis a11a12 a1nb1a21a22 a2nb2 an1an2 annbn displaystyle begin pmatrix a 11 a 12 a 1n b 1 a 21 a 22 a 2n b 2 a n1 a n2 a nn b n end pmatrix matrisi uzerinde aparmaq daha munasib olur Bele matris genislenmis matris adlanir Menbehttp brain ilkaddimlar com login html 2017 05 25 at the Wayback Machine
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State