Paralel xətlər

Paralel xətlər (q.yun. παράλληλος hərfi mənada "yan-yana dayanan, digəri boyunca qaçan") — planimetriyada kəsişməyən düz xətlər. Stereometriyada iki xətt eyni müstəvidə yerləşirsə və kəsişmirsə, paralel adlanır.

Paralel xətlər çəkmək üçün xətkeş

Evklid həndəsəsində

Rəsmlərdə paralel xətlər eyni istiqamətlənmiş oxlarla qeyd olunur.

Evklid həndəsəsində paralel xətlər eyni müstəvidə yerləşən və kəsişməyən xətlərdir. Tərifin başqa variantında üst-üstə düşən xətlər də paralel hesab olunur .

Sonuncu tərifin üstünlüyü ondan ibarətdir ki, paralellik ekvivalentlik münasibətinə çevrilir .

Xətlərin paralelliyi 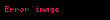${\displaystyle m}$ və ${\displaystyle n}$ adətən aşağıdakı kimi qeyd olunur: ${\displaystyle m\parallel n.}$

Xassələri

• Xəttdə olmayan hər hansı bir nöqtə vasitəsilə verilənə paralel bir xətt çəkə bilərsiniz və üstəlik, yalnız bir xətt. Bu ifadənin sonuncu hissəsi Evklidin məşhur beşinci postulatıdır. Beşinci postulatın rədd edilməsi Lobaçevski həndəsəsinə gətirib çıxarır.
• Bir xətt paralel xətlərdən birini kəsirsə, o, digərini də kəsir (belə bir xətt sekant adlanır). Bu vəziyyətdə, bəzi xarakterik cütlərin xüsusi adları və xüsusiyyətləri olan 8 bucaq yaranır:
  • Uyğun bucaqlar bərabərdir (şək. 1).
  • Çarpaz bucaqlar bərabərdir (şəkil 2).
  • Daxili birtərəfli bucaqlar 180°-ə qədər toplanır (şəkil 3).

Şəkil 1: Uyğun bucaqlar bərabərdir, 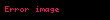${\displaystyle \alpha =\alpha _{1}}$ .	Şəkil 2: Daxili çarpaz bucaqlar bərabərdir, 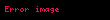${\displaystyle \alpha =\gamma _{1}}$ .	Şəkil 3: Birtərəfli bucaqlar tamamlayıcıdır, 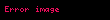${\displaystyle \alpha +\delta _{1}=180^{\circ }}$ .

• Əgər üst-üstə düşən xətləri paralel hesab etsək, onda paralellik bütün xətlər toplusunu bir-birinə paralel xətlər sinfinə ayıran ikili ekvivalentlik münasibəti olacaqdır.
• Müəyyən bir xəttdən müəyyən sabit məsafədə, onun bir tərəfində yerləşən müstəvidəki nöqtələr çoxluğu verilmiş birinə paralel bir xəttdir.

Lobaçevski həndəsəsində

Puankare modelində paralel xətlər: iki yaşıl xətt mavi xəttə bərabərtərəfli (asimptotik paralel) və bənövşəyi xətt ona ultraparaleldir.

Lobaçevski həndəsəsində ${\displaystyle C}$ nöqtəsi vasitəsilə müstəvidə bu xəttdən kənarda ${\displaystyle AB}$ ilə kəsişməyən sonsuz sayda düz ${\displaystyle AB}$ xətlər var. Düz ${\displaystyle CE}$ bərabərtərəfli xətt adlanır ${\displaystyle AB}$ olan istiqamətdə ${\displaystyle A}$-dan ${\displaystyle B}$-yə istiqamətlənir, Əgər:

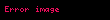
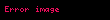
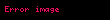
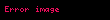
1. ${\displaystyle B}$ və ${\displaystyle E}$ nöqtələri ${\displaystyle AC}$ düz xəttin bir tərəfində uzanırsa ;
2. ${\displaystyle CE}$ düz xətti ${\displaystyle AB}$-ni kəsmir, lakin ${\displaystyle ACE}$ bucağı daxilində keçən istənilən şüa ${\displaystyle AB}$ şüasını kəsirsə.

Düz xətt eyni şəkildə müəyyən edilir 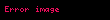${\displaystyle AB}$ olan istiqamətdə ${\displaystyle B}$-dən ${\displaystyle A}$-ya .

Bərabər tərəfli xətlərə asimptotik paralel və ya sadəcə paralel deyilir. Bu xətlə kəsişməyən bütün digər xətlər ultraparalel və ya divergent adlanır .

İstinadlar

1. Земляков А. Н. Аксиоматический подход к геометрии (тезисы). 2001.
2. Адамар Ж. Элементарная геометрия. М. 1948. 52.
3. Введение в современную математику (Начальные понятия). М.: Наука. 1965. 259.
4. "Математический справочник". 2016-09-23 tarixində arxivləşdirilib. İstifadə tarixi: 2016-07-08.