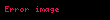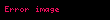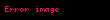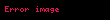Nyuton üsulu (həmçinin Nyuton-Rafson üsulu) — riyazi analizdə İsaak Nyuton və adına adlandırılmış, real dəyərə malik funksiyaların köklərinin ardıcıl olaraq daha yaxşı həllini tapmaq üsulu. Bu, kökün tapılması alqoritmlərindən biridir.
Nyuton üsulunun bir dəyişənlə tətbiqi aşağıdakı kimidir:
Bu üsul x dəyişəni olan f funksiyası, həmin funksiyanın f ′ törəməsi və f funksiyasının kökü kimi ilkin x0 fərziyyəsi ilə başlayır. Əgər bu funksiya formulanın törəməsindəki fərziyyələri qane edirsə və ilkin fərz edilən həll yaxındırsa, o zaman x1 daha yaxşı təxmini həll tapmaq üçün
istifadə edilir.
Həndəsi olaraq, (x1, 0), (x0, f (x0))-də f funksiyasının x oxu ilə kəsişməsidir
Bu proses daha dəqiq həll tapılana kimi aşağıdakı kimi davam etdirilir:
Təsviri
İkinci tərtib törəmənin köməyi ilə minimumun axtarılması üsullarına iki tərtibli üsullar deyilir. Bu üsullarda funksiyanın Teylor sırasına ayrılışında kvadratik hissədən istifadə edilir. Nyuton üsulu da məhz ikinci tərtib üsullara, yəni minimallaşdırılan funksiyanın ikinci tərtib törəmələrindən istifadə edilən üsullara aiddir. Bu üsulda da məqsəd funksiyanın Teylor ayrılışının kvadratik hissəsindən istifadə etməkdir. Teylor ayrılışının kvadratik hissəsi funksiyanı bu ayrılışın xətti hissəsinə nisbətən daha dəqiq approksimasiya etdiyindən gözləmək olar ki, ikinci tərtib üsullar birinci tərtib üsullara nisbətən daha sürətlə yığılır. Tətbiqi məsələlərin həlli göstərir ki, Nyuton üsulu çox sürətlə yığılır.
Nümunə
Ədədin kvadrat kökünün tapılması məsələsinə baxaq. Nyuton üsulu kvadrat kökün tapılması üsullarından biridir.
Məsələn, əgər 612-nin kökünü tapmaq istəyiriksə, o zaman bu məsələ belə yazıla bilər
Nyuton üsulu ilə funksiyanın yazılışı belədir
və onun törəməsi
İlkin fərziyyə kimi 10 ədədini götürsək, Nyuton üsulu ilə hesablama ardıcıllığı belə olacaq
burada düzgün onluq kəsr ədədlərinin altından xətt çəkilib. Bir neçə təkrarlamadan sonra nəticənin dəqiqliyi də artır.
Proqramlaşdırılması
Python
''' funksiyanın test edilməsi def f(x): return x**2 - 17 def f1(x): return 2*x ''' def newtons_method(x0, f, f1, e): #f1 - törəmə x0 = float(x0) while True: x1 = x0 - (f(x0) / f1(x0)) if abs(x1 - x0) < e: return x1 x0 = x1 PHP
<?php // PHP 5.4 function newtons_method( $a = -1, $b = 1, $f = function($x) { return pow($x, 4) - 1; }, $derivative_f = function($x) { return 4 * pow($x, 3); }, $eps = 1E-3) { $xa = $a; $xb = $b; $iteration = 0; while (abs($xb) > $eps) { $p1 = $f($xa); $q1 = $derivative_f($xa); $xa -= $p1 / $q1; $xb = $p1; ++$iteration; } return $xa; } Octave
function res = nt() eps = 1e-7; x0_1 = [-0.5,0.5]; max_iter = 500; xopt = new(@resh, eps, max_iter); xopt endfunction function a = new(f, eps, max_iter) x=-1; p0=1; i=0; while (abs(p0)>=eps) [p1,q1]=f(x); x=x-p1/q1; p0=p1; i=i+1; end i a=x; endfunction function[p,q]= resh(x) % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1; p=-25*x.^4+16*x.^3-36*x.^2+22*x-2; q=-100*x.^3+48*x.^2-72*x+22; endfunction С
#include <stdio.h> #include <math.h> #define eps 0.000001 double fx(double x) { return x*x-17;} // hesablanan funksiya double dfx(double x) { return 2*x;} // törəmə funksiya typedef double(*function)(double x); // tapşırıq tipi function double solve(function fx, function dfx, double x0) { double x1 = x0 - fx(x0)/dfx(x0); // birinci approksimasiya while (fabs(x1-x0)>eps) { // 0.000001 dəqiqliyinə çatana kimi x0 = x1; x1 = x1 - fx(x1)/dfx(x1); // növbəti approksimasiya } return x1; } int main () { printf("%f\n",solve(fx,dfx,4)); // ekrana verilməsi return 0; } C++
typedef double (*function)(double x); double TangentsMethod(function f, function df, double xn, double eps) { double x1 = xn - f(xn)/df(xn); double x0 = xn; while(abs(x0-x1) > eps) { x0 = x1; x1 = x1 - f(x1)/df(x1); } return x1; } //İlkin appoksimasiya seçimi xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A; double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Sizin funksiya double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Birinci dərəcəli törəmə double My2Derivative(double x) { return (20*pow(x, 3)); } //İkinci dərəcəli törəmə //Funksiyanın çağrılması nümunəsi double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1) İstinadlar
Xarici keçidlər
- Weisstein, Eric W. Newton's Method (ing.) Wolfram saytında.
- Newton's method, Citizendium.
- Mathews, J., The Accelerated and Modified Newton Methods, Course notes. Arxivləşdirilib 2019-05-24 at the Wayback Machine
- Wu, X., Roots of Equations, Course notes.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Nyuton usulu hemcinin Nyuton Rafson usulu riyazi analizde Isaak Nyuton ve adina adlandirilmis real deyere malik funksiyalarin koklerinin ardicil olaraq daha yaxsi hellini tapmaq usulu Bu kokun tapilmasi alqoritmlerinden biridir Nyuton usulunun bir deyisenle tetbiqi asagidaki kimidir Bu usul x deyiseni olan f funksiyasi hemin funksiyanin f toremesi ve f funksiyasinin koku kimi ilkin x0 ferziyyesi ile baslayir Eger bu funksiya formulanin toremesindeki ferziyyeleri qane edirse ve ilkin ferz edilen hell yaxindirsa o zaman x1 daha yaxsi texmini hell tapmaq ucun x1 x0 f x0 f x0 displaystyle x 1 x 0 frac f x 0 f x 0 istifade edilir Hendesi olaraq x1 0 x0 f x0 de f funksiyasinin x oxu ile kesismesidir Bu proses daha deqiq hell tapilana kimi asagidaki kimi davam etdirilir xn 1 xn f xn f xn displaystyle x n 1 x n frac f x n f x n TesviriIkinci tertib toremenin komeyi ile minimumun axtarilmasi usullarina iki tertibli usullar deyilir Bu usullarda funksiyanin Teylor sirasina ayrilisinda kvadratik hisseden istifade edilir Nyuton usulu da mehz ikinci tertib usullara yeni minimallasdirilan funksiyanin ikinci tertib toremelerinden istifade edilen usullara aiddir Bu usulda da meqsed funksiyanin Teylor ayrilisinin kvadratik hissesinden istifade etmekdir Teylor ayrilisinin kvadratik hissesi funksiyani bu ayrilisin xetti hissesine nisbeten daha deqiq approksimasiya etdiyinden gozlemek olar ki ikinci tertib usullar birinci tertib usullara nisbeten daha suretle yigilir Tetbiqi meselelerin helli gosterir ki Nyuton usulu cox suretle yigilir NumuneEdedin kvadrat kokunun tapilmasi meselesine baxaq Nyuton usulu kvadrat kokun tapilmasi usullarindan biridir Meselen eger 612 nin kokunu tapmaq isteyirikse o zaman bu mesele bele yazila biler x2 612 displaystyle x 2 612 Nyuton usulu ile funksiyanin yazilisi beledir f x x2 612 displaystyle f x x 2 612 ve onun toremesi f x 2x displaystyle f x 2x Ilkin ferziyye kimi 10 ededini gotursek Nyuton usulu ile hesablama ardicilligi bele olacaq x1 x0 f x0 f x0 10 102 6122 10 35 6x2 x1 f x1 f x1 35 6 35 62 6122 35 6 2 6 395505617978 x3 24 7 90635492455 x4 24 7386 88294075 x5 24 7386337537 67 displaystyle begin matrix x 1 amp amp x 0 dfrac f x 0 f x 0 amp amp 10 dfrac 10 2 612 2 times 10 amp amp 35 6 qquad qquad qquad quad x 2 amp amp x 1 dfrac f x 1 f x 1 amp amp 35 6 dfrac 35 6 2 612 2 times 35 6 amp amp underline 2 6 395 505 617 978 dots x 3 amp amp vdots amp amp vdots amp amp underline 24 7 90 635 492 455 dots x 4 amp amp vdots amp amp vdots amp amp underline 24 738 6 88 294 075 dots x 5 amp amp vdots amp amp vdots amp amp underline 24 738 633 753 7 67 dots end matrix burada duzgun onluq kesr ededlerinin altindan xett cekilib Bir nece tekrarlamadan sonra neticenin deqiqliyi de artir ProqramlasdirilmasiPython funksiyanin test edilmesi def f x return x 2 17 def f1 x return 2 x def newtons method x0 f f1 e f1 toreme x0 float x0 while True x1 x0 f x0 f1 x0 if abs x1 x0 lt e return x1 x0 x1 PHP lt php PHP 5 4 function newtons method a 1 b 1 f function x return pow x 4 1 derivative f function x return 4 pow x 3 eps 1E 3 xa a xb b iteration 0 while abs xb gt eps p1 f xa q1 derivative f xa xa p1 q1 xb p1 iteration return xa Octave function res nt eps 1e 7 x0 1 0 5 0 5 max iter 500 xopt new resh eps max iter xopt endfunction function a new f eps max iter x 1 p0 1 i 0 while abs p0 gt eps p1 q1 f x x x p1 q1 p0 p1 i i 1 end i a x endfunction function p q resh x p 5 x 5 4 x 4 12 x 3 11 x 2 2 x 1 p 25 x 4 16 x 3 36 x 2 22 x 2 q 100 x 3 48 x 2 72 x 22 endfunction S include lt stdio h gt include lt math h gt define eps 0 000001 double fx double x return x x 17 hesablanan funksiya double dfx double x return 2 x toreme funksiya typedef double function double x tapsiriq tipi function double solve function fx function dfx double x0 double x1 x0 fx x0 dfx x0 birinci approksimasiya while fabs x1 x0 gt eps 0 000001 deqiqliyine catana kimi x0 x1 x1 x1 fx x1 dfx x1 novbeti approksimasiya return x1 int main printf f n solve fx dfx 4 ekrana verilmesi return 0 C typedef double function double x double TangentsMethod function f function df double xn double eps double x1 xn f xn df xn double x0 xn while abs x0 x1 gt eps x0 x1 x1 x1 f x1 df x1 return x1 Ilkin appoksimasiya secimi xn MyFunction A My2Derivative A gt 0 B A double MyFunction double x return pow x 5 x 0 2 Sizin funksiya double MyDerivative double x return 5 pow x 4 1 Birinci dereceli toreme double My2Derivative double x return 20 pow x 3 Ikinci dereceli toreme Funksiyanin cagrilmasi numunesi double x TangentsMethod MyFunction MyDerivative xn 0 1 IstinadlarXarici kecidlerWeisstein Eric W Newton s Method ing Wolfram saytinda Newton s method Citizendium Mathews J The Accelerated and Modified Newton Methods Course notes Arxivlesdirilib 2019 05 24 at the Wayback Machine Wu X Roots of Equations Course notes
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans