Bu məqaləni lazımdır. |
Miller indeksləri-üç tam ədəddən ibarət, kristal qəfəsdə atom müstəvilərini və istiqamətləri işarə etmək üçün istifadə olunan bir simvol

Bazis vektorları olan bir qəfəs üçün Miller indekslərini təyin edək. Bunun üçün kordinat oxlarını uyğun olaraq vektorları boyunca və qəfəsin ixtiyari bir düyün nöqtəsini koordinat başlanğıcı olaraq seçək.
Belə bir koordinat sistemində, koordinat oxlarından və parçaları kəsən bir müstəvi aşağıda Şəkil1-də ştrixlənmiş olaraq göstərilmişdir. Bu, miller indekslərini təyin etmək istədiyimiz atom müstəvisi olsun
Kristalloqrafiyada qəbul olunmuş qəfəs sabitləri -lərin köməyiylə parçalarının yerinə adsız və ədədlərini alıb, onların tərs qiymətlərini şəkildə yazaraq atom müstəvisinin Miller indekslərini əldə etmək olar. Göstərmək olar ki, bu şəkildə təyin olunmuş Miller indekslərini həmişə üç tam ədədlə ifadə etmək mümkündür və onun şəklində yazılması qəbul edilmişdir . Doğrudan da nisbətlərini alıb onları üç ən kiçik tam ədədlərin nisbətinə gətirərək, şəkildə yazmaq olar.
Məsələn, tutaq ki atom müstəvisi 1istiqamətindəki oxdan parçasınə və istiqamətlərində isə, uyğun olaraq parçalarını kəsmmişdir. O zaman belə bir müstəvinin Miller indeksləri, qəbul olunan qaydada , yəni üç tam ədədolacaq.
Sadə kubik qəfəsdə bir neçə atom müstəvilərinin Miller indeksləri Şəkil2-də verilmişdir.

Əgər parçalarından hər hansı biri mənfi olarsa, o işarə uyğun Miller indeksinin üstündə yazılır. Deyək ki, istiqamətlərində uyğun olaraq parçaları kəsilmişdir. O halda, bu atom müstəvisinin Miller indeksləri şəklində yazılar.
Fiziki ekvivalent müstəvilərin Miller indeksləri kimi işarə olunur. Məsələn simvolu kubik qəfəsin altı elementar özəyi olan kubun üzündən keçən atom müstəvilərinin indekslərini göstərir.
Miller indekslərnin kristalloqrafyada və beləliklə bərk cisimlər fizikasında yerini və əhəmiyyətini müəyyən edən iki teorem haqqında söz açmaq yerinə düşər. Bir kristal qəfəsin uyğun tərs qəfəs bazis vektorları və tam ədədlər olmaqla tərs qəfəs köçürmə vektorları ilə atom müstəvilərinə baxaq.
Teorem1. Əgər isə vektoru atom müstəvisinə perpendikulyardır.
Teorem2. atom müstəviləri ailəsində iki qonşu müstəvi arasındakı məsafə bərabərdir.
Bu iki teorem (onları isbatsız veririk) bərk cisimlərin kristal quruluşunun təcrübi tədqiqat metodlarının əsasını təşkil edirlər. Xüsusiylə də məşhur Breqq formulu ikinci teoremin birbaşa nəticəsidir. Bu teoremin köməyi lə birbaşa qəfəs sabitlərini tapmaq olur. Məsələn kubuk qəfəslərdə müstəviləri üçün iki qonşu müstəvi arasındakı məsafə -tapaq. Bunun üçün -vektorunun ədəd qiymətini bilmək lazımdır:
Sadə kub üçün . Yəni ;
Burdan alınır ki, bu da kubik qəfəsin qəfəs sabitidir.
Miller indekslərinin tətbiqi əhəmiyyəti bununla bitmir. Rentgen şüalarının kristal qəfəsdən səpilməsi zamanı səpilən şüaların intensivliyi Miller indeksləriylə təyin olur . Məsələn həcmə mərkəzləşmiş kubda miller indekslərinin cəmi tək ədəd olan müstəvilərdən səpilən şüaların intensivliyi sıfır olar.
Kristal qəfəsdə hər hansı bir düyündən (atomdan) keçən düz xətt üçün də üç tam ədəddən ibarət bir simvol yazmaq olur ki, ona da istiqamətin Miller indeksləri deyilir. İstiqamətin Miller indeksləri üçün, parçaları olaraq, uyğun istiqamətin ixtiyari bir nöqtəsinin koordinat oxlarına proyeksiyalarını -lərə bölərək əldə edilən üç adsız ədəd şəkildə yazılır. Onların da nisbəti ən kiçik tam ədədlər olan -ə gətirilir və simvolu əldə edilir. Məsələn kubik qəfəsdə vektoru istiqamətinin Miller indeksini yazaq. Bu istiqamətdə ixtiyari bir nöqtənin koordinat oxlarına proyeksiyaları və istiqamətlərinə sıfır, istiqamətinə isə olsun. Onda bu istiqamətin Miller indeksləri olacaq.
İstiqamətində Miller indekslərindən hər hansı biri mənfi isə o işarə uyğun indeksin üstündə yazılır. Məsələn simvolu seçilmiş koordinat sistemində koordinatları olan bir nöqtədən keçən düz xəttin Miller indeksləridir- .
Fiziki ekvivalent istiqamətlər şəklində işarə olunurlar. Məsələn kubik qəfəsdə hər hansı bir düyündən keçən və vektorlarına paralel istiqamətlər olaraq-üçü müsbət və üçü mənfi olmaqla altı istiqamətin Miller indekslərinin məcmusunu göstərir.
Burada kubik qəfəslər üçün atom müstəvisiylə istiqamətinn bir-birinə perpendikulyar olduğunu qeyd etməkdə fayda var. Bu xassə digər kristal qəfəslər üçün ümumiyyətlə doğru deyil.
Miller indekslərinin bir xassəsini də qeyd edək: müstəvinin və ya istiqamətin Miller indeksləri eyni zamanda həmin müstəvidə (istiqamətdə) səthin vahid sahəsində (vahid uzunluğunda) yerləşən atom sayını da (başqa sözlə atom sıxlığını) göstərir . Məsələn simvolu kubik qəfəsdə vektoruna perpendikulyar olan atom müstəvisidir və bu müstəvi elementar özəyi ölçülü kvadrat olan ikiölçülü bir qəfəsdir. O zaman hər elementar özəkdə bir atom yer aldığına görə atom sıxlığı olaraq əldə edilir (burada elementar özəyin, yəni kvadratın sahəsidir), simvolu isə vektoruna paralel və vektoruna perpendikulyar atom müstəvisinin Miller indeksi, bu müstəvi isə tərəfləri və olan kvadrat üzərində qurulmuş ikiölçülü bir qəfəsdir. Deməli bu qəfəsin elementar özəyinin sahəsi və atom sıxlığı -a bərabərdir. Beləliklə , atom müstəviləri üçün atom sıxlığını (sadə qəfəslər üçün) aşağıdakı kimi yazmaq olar:
Yəni hökm etmək olar ki, atom müstəvisində atom sıxlığı vuruğu ilə mütənasibdir. Başqa sözlə Miller indekslərinin ən kiçik qiymətlərinə atom sıxlığı böyük olan müstəvilər uyğun gəlir .
Ədəbiyyat
- M. Əsgərov. “Bərk Cisimlər Fizikası”, Bakı 2001.*
- B.M. Əsgərov. “Bərk Cisimlərin Nəzəriyyəsi”, Bakı 2013.*
- А.И. Ансельм «Введение в теорию полупроводников», Москва 1978.*
- Дж. Займан «Принципы теории твердого тело» издательство Мир 1966*
İstinadlar
- http://elibrary.bsu.az/books_aysel/N_355.pdf[ölü keçid].
- http://elibrary.bsu.az/books_rax/N_108.pdf 2017-11-18 at the Wayback Machine.
- http://ikfia.ysn.ru/images/doc/Solid_State_Physics/Anselm1978ru.pdf[ölü keçid].
- http://booksshare.net/books/physics/zayman-dj/1966/files/principiteoriitverdogotela1966.pdf 2018-12-22 at the Wayback Machine.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqaleni vikilesdirmek lazimdir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Miller indeksleri uc tam ededden ibaret kristal qefesde atom mustevilerini ve istiqametleri isare etmek ucun istifade olunan bir simvolSekil1 Bazis vektorlari a 1 a 2 a 3 displaystyle vec a 1 vec a 2 vec a 3 olan bir qefes ucun Miller indekslerini teyin edek Bunun ucun kordinat oxlarini uygun olaraq a i displaystyle vec a i vektorlari boyunca ve qefesin ixtiyari bir duyun noqtesini koordinat baslangici olaraq secek Bele bir koordinat sisteminde koordinat oxlarindan s1 s2 displaystyle s 1 s 2 ves3 displaystyle s 3 parcalari kesen bir mustevi asagida Sekil1 de strixlenmis olaraq gosterilmisdir Bu miller indekslerini teyin etmek istediyimiz atom mustevisi olsun Kristalloqrafiyada qebul olunmus qefes sabitleri a b c displaystyle a b c lerin komeyiyle si displaystyle s i parcalarinin yerine adsiz s1a s2b displaystyle frac s 1 a frac s 2 b ve s3c displaystyle frac s 3 c ededlerini alib onlarin ters qiymetlerini as1bs2cs3 displaystyle Bigl frac a s 1 frac b s 2 frac c s 3 Bigr sekilde yazaraq atom mustevisinin Miller indekslerini elde etmek olar Gostermek olar ki bu sekilde teyin olunmus Miller indekslerini hemise uc tam ededle ifade etmek mumkundur ve onun hkl displaystyle hkl seklinde yazilmasi qebul edilmisdir Dogrudan da as1 bs2 cs3 displaystyle frac a s 1 frac b s 2 frac c s 3 nisbetlerini alib onlari uc en kicik tam ededlerin nisbetine getirerek as1 bs2 cs3 h k l displaystyle frac a s 1 frac b s 2 frac c s 3 h k l sekilde yazmaq olar Meselen tutaq ki atom mustevisi a 1 displaystyle vec a 1 1istiqametindeki oxdan a2 displaystyle frac a 2 parcasine ve a 2 a 3 displaystyle vec a 2 vec a 3 istiqametlerinde ise uygun olaraq b c displaystyle b c parcalarini kesmmisdir O zaman bele bir mustevinin Miller indeksleri qebul olunan qaydada as1bs2cs3 aa 2bccc 211 displaystyle Biggl frac a s 1 frac b s 2 frac c s 3 Biggr Biggl frac a a 2 frac b c frac c c Biggr 211 yeni uc tam ededolacaq Sade kubik qefesde bir nece atom mustevilerinin Miller indeksleri Sekil2 de verilmisdir Sekil2 Eger si displaystyle s i parcalarindan her hansi biri menfi olarsa o isare uygun Miller indeksinin ustunde yazilir Deyek ki a 1 a 2 a 3 displaystyle vec a 1 vec a 2 vec a 3 istiqametlerinde uygun olaraq s1 a s2 b s3 c displaystyle s 1 a s 2 b s 3 c parcalari kesilmisdir O halda bu atom mustevisinin Miller indeksleri aab bcc 1 1 1 11 1 displaystyle Biggl frac a a frac b b frac c c Biggr 1 1 1 1 bar 1 1 seklinde yazilar Fiziki ekvivalent mustevilerin Miller indeksleri hkl displaystyle hkl kimi isare olunur Meselen 100 displaystyle 100 simvolu kubik qefesin alti elementar ozeyi olan kubun uzunden kecen atom mustevilerinin indekslerini gosterir Miller indekslernin kristalloqrafyada ve belelikle berk cisimler fizikasinda yerini ve ehemiyyetini mueyyen eden iki teorem haqqinda soz acmaq yerine duser Bir kristal qefesin uygun ters qefes bazis vektorlari bi displaystyle b i ve tam ededler gi displaystyle g i olmaqla b g g1b 1 g2b 2 g3b 3 displaystyle vec b g g 1 vec b 1 g 2 vec b 2 g 3 vec b 3 ters qefes kocurme vektorlari ile hkl displaystyle hkl atom mustevilerine baxaq Teorem1 Eger g1 g2 g3 h k l displaystyle g 1 g 2 g 3 h k l ise b g displaystyle vec b g vektoru hkl displaystyle hkl atom mustevisine perpendikulyardir Teorem2 hkl displaystyle hkl atom mustevileri ailesinde iki qonsu mustevi arasindaki mesafe d hkl 2p b hkl displaystyle d hkl frac 2 pi vec b hkl beraberdir Bu iki teorem onlari isbatsiz veririk berk cisimlerin kristal qurulusunun tecrubi tedqiqat metodlarinin esasini teskil edirler Xususiyle de meshur Breqq formulu ikinci teoremin birbasa neticesidir Bu teoremin komeyi le birbasa qefes sabitlerini tapmaq olur Meselen kubuk qefeslerde 100 displaystyle 100 mustevileri ucun iki qonsu mustevi arasindaki mesafe d 100 displaystyle d 100 tapaq Bunun ucun b 100 displaystyle vec b 100 vektorunun eded qiymetini bilmek lazimdir b 100 1 b 1 0 b 2 0 b 3 b 1 displaystyle vec b 100 1 cdot vec b 1 0 cdot vec b 2 0 cdot vec b 3 vec b 1 Sade kub ucun b 1 2p a 2a 3 a3 2pa2a 1 displaystyle vec b 1 frac 2 pi vec a 2 vec a 3 a 3 frac 2 pi a 2 vec a 1 Yeni b 100 2pa displaystyle vec b 100 frac 2 pi a Burdan d 100 2p2p a a displaystyle d 100 frac 2 pi 2 pi a a alinir ki bu da kubik qefesin qefes sabitidir Miller indekslerinin tetbiqi ehemiyyeti bununla bitmir Rentgen sualarinin kristal qefesden sepilmesi zamani sepilen sualarin intensivliyi Miller indeksleriyle teyin olur Meselen hecme merkezlesmis kubda miller indekslerinin cemi tek eded olan mustevilerden sepilen sualarin intensivliyi sifir olar Kristal qefesde her hansi bir duyunden atomdan kecen duz xett ucun de uc tam ededden ibaret bir simvol yazmaq olur ki ona da istiqametin Miller indeksleri deyilir Istiqametin Miller indeksleri ucun s1 s2 s3 displaystyle s 1 s 2 s 3 parcalari olaraq uygun istiqametin ixtiyari bir noqtesinin koordinat oxlarina proyeksiyalarini a b c displaystyle a b c lere bolerek elde edilen uc adsiz eded s1as2bs3c displaystyle Biggl frac s 1 a frac s 2 b frac s 3 c Biggr sekilde yazilir Onlarin da nisbeti en kicik tam ededler olan h k l displaystyle h k l e getirilir ve h k l displaystyle h k l simvolu elde edilir Meselen kubik qefesde a 1 displaystyle vec a 1 vektoru istiqametinin Miller indeksini yazaq Bu istiqametde ixtiyari bir noqtenin koordinat oxlarina proyeksiyalari a 2 displaystyle vec a 2 ve a 3 displaystyle vec a 3 istiqametlerine sifir a 1 displaystyle vec a 1 istiqametine ise a displaystyle a olsun Onda bu istiqametin Miller indeksleri aa0b0c 100 displaystyle Biggl frac a a frac 0 b frac 0 c Biggr 100 olacaq Istiqametinde Miller indekslerinden her hansi biri menfi ise o isare uygun indeksin ustunde yazilir Meselen 01 1 displaystyle 0 bar 1 1 simvolu secilmis koordinat sisteminde koordinatlari 0 b c displaystyle 0 b c olan bir noqteden kecen duz xettin Miller indeksleridir 0a bbcc 01 1 displaystyle Biggl frac 0 a frac b b frac c c Biggr 0 bar 1 1 Fiziki ekvivalent istiqametler h k l displaystyle langle h k l rangle seklinde isare olunurlar Meselen kubik qefesde her hansi bir duyunden kecen ve a i displaystyle vec a i vektorlarina paralel istiqametler 1 0 0 displaystyle langle 1 0 0 rangle olaraq ucu musbet ve ucu menfi olmaqla alti istiqametin Miller indekslerinin mecmusunu gosterir Burada kubik qefesler ucun h k l displaystyle h k l atom mustevisiyle h k l displaystyle h k l istiqametinn bir birine perpendikulyar oldugunu qeyd etmekde fayda var Bu xasse diger kristal qefesler ucun umumiyyetle dogru deyil Miller indekslerinin bir xassesini de qeyd edek mustevinin ve ya istiqametin Miller indeksleri eyni zamanda hemin mustevide istiqametde sethin vahid sahesinde vahid uzunlugunda yerlesen atom sayini da basqa sozle atom sixligini gosterir Meselen 100 displaystyle 100 simvolu kubik qefesde a i displaystyle vec a i vektoruna perpendikulyar olan atom mustevisidir ve bu mustevi elementar ozeyi a displaystyle a olculu kvadrat olan ikiolculu bir qefesdir O zaman her elementar ozekde bir atom yer aldigina gore atom sixligi 1s0 1a2 displaystyle frac 1 s 0 frac 1 a 2 olaraq elde edilir burada s0 a2 displaystyle s 0 a 2 elementar ozeyin yeni kvadratin sahesidir 110 displaystyle 110 simvolu ise a 3 displaystyle vec a 3 vektoruna paralel ve a 1 a 2 displaystyle vec a 1 vec a 2 vektoruna perpendikulyar atom mustevisinin Miller indeksi bu mustevi ise terefleri a displaystyle a ve 2a displaystyle sqrt 2 a olan kvadrat uzerinde qurulmus ikiolculu bir qefesdir Demeli bu qefesin elementar ozeyinin sahesi s0 2a2 displaystyle s 0 sqrt 2 a 2 ve atom sixligi 12a2 displaystyle frac 1 sqrt 2 a 2 a beraberdir Belelikle 100 displaystyle 100 110 displaystyle 110 atom mustevileri ucun atom sixligini sade qefesler ucun asagidaki kimi yazmaq olar 1h2 k2 l2a2 112 02 02a2 1a2 100 112 12 02a2 12a2 110 displaystyle frac 1 sqrt h 2 k 2 l 2 a 2 begin cases frac 1 sqrt 1 2 0 2 0 2 a 2 frac 1 a 2 100 frac 1 sqrt 1 2 1 2 0 2 a 2 frac 1 sqrt 2 a 2 110 end cases Yeni hokm etmek olar ki h k l displaystyle h k l atom mustevisinde atom sixligi 1h2 k2 l2 displaystyle frac 1 sqrt h 2 k 2 l 2 vurugu ile mutenasibdir Basqa sozle Miller indekslerinin en kicik qiymetlerine atom sixligi boyuk olan musteviler uygun gelir EdebiyyatM Esgerov Berk Cisimler Fizikasi Baki 2001 B M Esgerov Berk Cisimlerin Nezeriyyesi Baki 2013 A I Anselm Vvedenie v teoriyu poluprovodnikov Moskva 1978 Dzh Zajman Principy teorii tverdogo telo izdatelstvo Mir 1966 Istinadlarhttp elibrary bsu az books aysel N 355 pdf olu kecid http elibrary bsu az books rax N 108 pdf 2017 11 18 at the Wayback Machine http ikfia ysn ru images doc Solid State Physics Anselm1978ru pdf olu kecid http booksshare net books physics zayman dj 1966 files principiteoriitverdogotela1966 pdf 2018 12 22 at the Wayback Machine
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
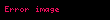
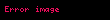
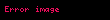
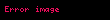
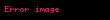

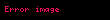
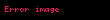
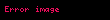
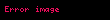
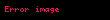
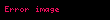
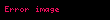
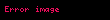
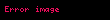
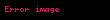

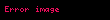
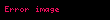
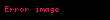
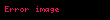
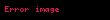
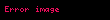
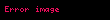
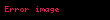
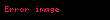
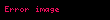
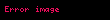
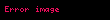
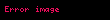
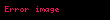
![{\displaystyle {\vec {b}}_{1}={\frac {2\pi [{\vec {a}}_{2}{\vec {a}}_{3}]}{a_{3}}}={\frac {2\pi }{a^{2}}}{\vec {a}}_{1}}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4M05HWTFaV001T1RjMk5HTTVZVGN3WWpVM09URXpOVGcwWXpOa1pqUTJNV00zWkRkbU9UazMuc3Zn.svg)
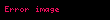

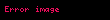
![{\displaystyle {\Biggl [}{\frac {s_{1}}{a}}{\frac {s_{2}}{b}}{\frac {s_{3}}{c}}{\Biggr ]}}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5bU5qQTNOMlpqWm1Zd1ptRTJOV1E1TW1FM1pESTVaR0k1TkRNME5qaGtZMlF4WmpBMFkyTmkuc3Zn.svg)
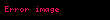
![{\displaystyle [h,k,l]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5a01EaGtaR0ZtTjJZelpUazBZbVkwTURJeE56aGhNREF4TVRZNE5qYzRZbUZpTVRCak9ESXguc3Zn.svg)
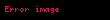
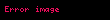

![{\displaystyle {\Biggl [}{\frac {a}{a}}{\frac {0}{b}}{\frac {0}{c}}{\Biggr ]}=[100]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5ak16UXhNRFZsTURoa1lUZ3hNV0U0T1RZd1pHSmtOMkV3WVRZNFpURTJNVEprT1RGbU5UaGsuc3Zn.svg)
![{\displaystyle [0{\bar {1}}1]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4NU1tVTBORFJpT0dKa01XWmxOMk14WWpGak9UQmpPV0ZtTkRKaU9EWTBOVGsyTWpNMk5tSmouc3Zn.svg)
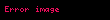
![{\displaystyle {\Biggl [}{\frac {0}{a}}{\frac {-b}{b}}{\frac {c}{c}}{\Biggr ]}=[0{\bar {1}}1]}](https://www.wikimedia.az-az.nina.az/image/aHR0cHM6Ly93d3cud2lraW1lZGlhLmF6LWF6Lm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4NVltRTJaRFEwWm1GbE5URTNNakZpT1RVNFptSXdOamxoTXpBMk1tRTVaVEEzTkRaallqWmwuc3Zn.svg)