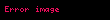Riyaziyyatda, Lejandr funksiyaları aşağıdakı Lejandr differensial tənliyinin dəqiq həlli şəklində meydana çıxır:
Bu funksiyalara məşhur fransiz riyaziyyatçısı Adrien Mari Lejandrın şərəfinə Lejandr funksiyaları adı verilmişdir. Yuxarıda göstərilən adi diferensial tənlik fizika və bir çox digər təbiət və texniki elm sahələrinin müxtəlif məsələlərinin izah edilməsi zamanı meydana çıxır və uğurla tətbiq edilir. Məsələn, Laplas tənliyinin (və uyğun xüsusi törəməli differensial tənliklərin) sferik koordinatlarda dəqiq həlli məhz bu funksiyalara gətirib çıxarır.
Lejandr diferensial tənliyi adi qüvvət sıraları üsulundan istifadə etməklə dəqiq həll edilə bilər. Bu tənlik x = ±1 qiymətlərində requlyar sinqulyar nöqtələrə malikdir. Bu səbəbdən də, ümumilkdə, qüvvət sıraları üsulu ilə tapilan həll əslində yalnız |x| < 1 şərti çərçivəsində doğrudur. n tam ədəd olduğu zaman isə, x = 1 qiymətində requlyar olan Pn(x) həlli, eyni zamanda, x = −1 qiymətində də requlyar olacaq ki, bu səbəbdən də bu həllin sonsuz sıra şəkli kəsilərək sonlu cəm şəklinə düşəcək (bağqa sözlə, çoxhədliyə çevriləcək).
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Riyaziyyatda Lejandr funksiyalari asagidaki Lejandr differensial tenliyinin deqiq helli seklinde meydana cixir ddx 1 x2 ddxPn x n n 1 Pn x 0 displaystyle d over dx left 1 x 2 d over dx P n x right n n 1 P n x 0 Bu funksiyalara meshur fransiz riyaziyyatcisi Adrien Mari Lejandrin serefine Lejandr funksiyalari adi verilmisdir Yuxarida gosterilen adi diferensial tenlik fizika ve bir cox diger tebiet ve texniki elm sahelerinin muxtelif meselelerinin izah edilmesi zamani meydana cixir ve ugurla tetbiq edilir Meselen Laplas tenliyinin ve uygun xususi toremeli differensial tenliklerin sferik koordinatlarda deqiq helli mehz bu funksiyalara getirib cixarir Lejandr diferensial tenliyi adi quvvet siralari usulundan istifade etmekle deqiq hell edile biler Bu tenlik x 1 qiymetlerinde requlyar sinqulyar noqtelere malikdir Bu sebebden de umumilkde quvvet siralari usulu ile tapilan hell eslinde yalniz x lt 1 serti cercivesinde dogrudur n tam eded oldugu zaman ise x 1 qiymetinde requlyar olan Pn x helli eyni zamanda x 1 qiymetinde de requlyar olacaq ki bu sebebden de bu hellin sonsuz sira sekli kesilerek sonlu cem sekline dusecek bagqa sozle coxhedliye cevrilecek
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans