Klassik mexanika fizikanın makroskopik cisimlərin hərəkətini izah eləyən sahəsidir. Fizikanın nəzəriyyələri arasında ən geniş yayılmışıdır. Əhatə etdiyi mövzulara isə, kütlə, təcil və qüvvə aiddir. Burada hadisələrin 3 ölçülü Evklid fəzasında baş verdiyini təsəvvür eləyirlər.
Klassik mexanikada çoxlu tənliklərdən istifadə olunur və başqa riyazi anlayışlardan da həmçinin. Məsələn, differensial tənliklər, Li qrupları, çoxqatlılar və erqodik nəzəriyyə və s. Bu səhifədə bunların arasında ən önəmlilərinin xülasəsi verilib
Bu məqalədə əsasən Nyuton mexanikasının düsturlarını təqdim eləyir. Klassik mexanikanın daha ümumi tərtibi üçün isə analtik mexanikaya baxın (Laqranj və Hamilton mexaniklarını əhatə eləyir).
Klassik mexanika
Kütlə və ətalət
| Kəmiyyət (geniş yayılmış adı/ları) | (Geniş yayılmış) simvolu/ları | Tənliyi | SI vahidləri | Ölçüsü |
|---|---|---|---|---|
| Xətti, səth, həcmi kütlə sıxlığı | λ yaxud μ (xüsuilə akustikada) xətti sıxlıq üçün, σ səth üçün, ρ həcm üçün. | 
| kg m−n, n = 1, 2, 3 | [M][L]−n |
| Kütlə momenti | m (Ümumi simvolu yoxdur) | Maddi nöqtə:
| kg m | [M][L] |
| Kütlə mərkəzi | rcom (Simvolu dəyişə bilər) | i-ncı kütlə momenti  Diskret kütlələr: Kütlələr silsiləsi: | m | [L] |
| 2 cisimli azalmış kütlə | m12, μ Kütlələr = m1 and m2 |  | kg | [M] |
| Ətalət momenti | I | Diskret kütlələr:
Kütlələr silsiləsi: | kg m2 | [M][L]2 |
| Kəmiyyət (geniş yayılmış adı/ları) | (Geniş yayılmış) simvolu/ları | Tənliyi | SI vahidləri | Ölçüsü |
|---|---|---|---|---|
| Moment | p |  | kg m s−1 | [M][L][T]−1 |
| Qüvvə | F |  | N = kg m s−2 | [M][L][T]−2 |
| İmpuls | J, Δp, I | 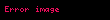 | kg m s−1 | [M][L][T]−1 |
| nöqtəsinə nəzərən bucaq momenti r0 | L, J, S | 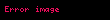 Most of the time we can set r0 = 0 if particles are orbiting about axes intersecting at a common point. | kg m2 s−1 | [M][L]2[T]−1 |
| Moment of a force about a position point r0, | τ, M |  | N m = kg m2 s−2 | [M][L]2[T]−2 |
| Angular impulse | ΔL (no common symbol) |  | kg m2 s−1 | [M][L]2[T]−1 |
Notes
- Section: Moments and center of mass[ölü keçid]
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Klassik mexanika fizikanin makroskopik cisimlerin hereketini izah eleyen sahesidir Fizikanin nezeriyyeleri arasinda en genis yayilmisidir Ehate etdiyi movzulara ise kutle tecil ve quvve aiddir Burada hadiselerin 3 olculu Evklid fezasinda bas verdiyini tesevvur eleyirler Klassik mexanikada coxlu tenliklerden istifade olunur ve basqa riyazi anlayislardan da hemcinin Meselen differensial tenlikler Li qruplari coxqatlilar ve erqodik nezeriyye ve s Bu sehifede bunlarin arasinda en onemlilerinin xulasesi verilib Bu meqalede esasen Nyuton mexanikasinin dusturlarini teqdim eleyir Klassik mexanikanin daha umumi tertibi ucun ise analtik mexanikaya baxin Laqranj ve Hamilton mexaniklarini ehate eleyir Klassik mexanikaKutle ve etalet Kemiyyet genis yayilmis adi lari Genis yayilmis simvolu lari Tenliyi SI vahidleri OlcusuXetti seth hecmi kutle sixligi l yaxud m xusuile akustikada xetti sixliq ucun s seth ucun r hecm ucun m ldℓ displaystyle m int lambda mathrm d ell m sdS displaystyle m iint sigma mathrm d S m rdV displaystyle m iiint rho mathrm d V kg m n n 1 2 3 M L nKutle momenti m Umumi simvolu yoxdur Maddi noqte m rm displaystyle mathbf m mathbf r m xi displaystyle x i m i 1Nrimi displaystyle mathbf m sum i 1 N mathbf r mathrm i m i xi displaystyle x i m r r xidr displaystyle mathbf m int rho left mathbf r right x i mathrm d mathbf r kg m M L Kutle merkezi rcom Simvolu deyise biler i nci kutle momenti mi rimi displaystyle mathbf m mathrm i mathbf r mathrm i m i Diskret kutleler rcom 1M irimi 1M imi displaystyle mathbf r mathrm com frac 1 M sum i mathbf r mathrm i m i frac 1 M sum i mathbf m mathrm i Kutleler silsilesi rcom 1M dm 1M rdm 1M rrdV displaystyle mathbf r mathrm com frac 1 M int mathrm d mathbf m frac 1 M int mathbf r mathrm d m frac 1 M int mathbf r rho mathrm d V m L 2 cisimli azalmis kutle m12 m Kutleler m1 and m2 m m1m2 m1 m2 displaystyle mu left m 1 m 2 right left m 1 m 2 right kg M Etalet momenti I Diskret kutleler I imi ri i ri 2m displaystyle I sum i mathbf m mathrm i cdot mathbf r mathrm i sum i left mathbf r mathrm i right 2 m Kutleler silsilesi I r 2dm r dm r 2rdV displaystyle I int left mathbf r right 2 mathrm d m int mathbf r cdot mathrm d mathbf m int left mathbf r right 2 rho mathrm d V kg m2 M L 2Kemiyyet genis yayilmis adi lari Genis yayilmis simvolu lari Tenliyi SI vahidleri OlcusuMoment p p mv displaystyle mathbf p m mathbf v kg m s 1 M L T 1Quvve F F dp dt displaystyle mathbf F mathrm d mathbf p mathrm d t N kg m s 2 M L T 2Impuls J Dp I J Dp t1t2Fdt displaystyle mathbf J Delta mathbf p int t 1 t 2 mathbf F mathrm d t kg m s 1 M L T 1noqtesine nezeren bucaq momenti r0 L J S L r r0 p displaystyle mathbf L left mathbf r mathbf r 0 right times mathbf p Most of the time we can set r0 0 if particles are orbiting about axes intersecting at a common point kg m2 s 1 M L 2 T 1Moment of a force about a position point r0 Torque t M t r r0 F dL dt displaystyle boldsymbol tau left mathbf r mathbf r 0 right times mathbf F mathrm d mathbf L mathrm d t N m kg m2 s 2 M L 2 T 2Angular impulse DL no common symbol DL t1t2tdt displaystyle Delta mathbf L int t 1 t 2 boldsymbol tau mathrm d t kg m2 s 1 M L 2 T 1NotesSection Moments and center of mass olu kecid
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans