Bu məqaləni lazımdır. |
Formal qrammatika — dedikdə elə qaydalar sistemi başa düşülür ki, onun vasitəsilə verilmiş formal dilin(yalnız bu dilin) düzgün sözləri qura bilir. Qrammatika vasitəsilə qurulan formal dilin sözlər çoxluğu sonlu, sonsuz, və ya boş çoxluq ola bilər. Qrammatika sözlər çoxluğunu ixtiyari qaydada qura, yaxud müəyyənləşdirə bilər. Beləliklə, qrammatika sözlərin daxili quruluşunun qanunlarını açıqlayır ki, bunlara sintaksis deyilir. Formal qrammatika— müəyyən sintaksis nəzəriyyə çərçivəsində qurulan qrammatik riyazi modeldir.
Formal qrammatikanın növləri
Alqoritmik nöqteyi-nəzərdən formal qrammatikaların aşağıdakı növləri var:
- Tanıyan qrammatikalar: Bu qrammatikalar bir növ elə qurğudur ki, bunun girişinə daxil olan söz verilmiş dilə aiddirsə, "hə", aid deyilsə- "yox" çap olunur.
- Sadalayan qrammatikalar: Bu qrammatikalar verilmiş dilin bütün sözlərini bir-bir çap etməklə(sadalamaqla) iş görür. Aydındır ki, dilin sözlərinin sayı sonsuz olarsa, qrammatika heç zaman dayanmayacaq. Ancaq qrammatikanı məcburi o zaman dayandırmaq olar ki, lazım olan söz çap olunmuşdur.
- Doğuran qrammatikalar: Bunlar elə "qurğu"dur ki, dilin lazımlı sözlərini qurur. Doğuran qrammatikaların müxtəlif variantlarını ABŞ riyaziyyatçısı və linqivisti keçən əsrin 50-ci illərindən etibarən yaratmağa başlamışdır. Bir zamanlar hətta bu qrammatikalar təbii dillərin qurulması üçün istifadə oluna bilən kimi fərz olunurdu, lakin zaman bunların təbii dillər sahəsində tətbiqi imkanlarını sübut etmədi. Hazırda doğuran qrammatikalar, əsasən, formal dillərin(proqramlaşdırma dillərinin) sintaksisinin qurulmasında müvəffəqiyyətlə istifadə olunur.
Doğuran qrammatika
Tərif: Formal doğuran qrammatika dedikdə 4 obyektdən ibarət bir formal G={V, W, I, P} sistemi başa düşülür ki, burada V={a1, a2,…, am}- terminal simvollar əlifbası, V={A1, A2,…, An}- qeyri-terminal simvollar əlifbasıdır. Bunların kəsişmədiyi fərz olunur: 

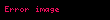
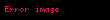
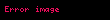
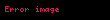

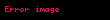

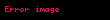
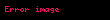

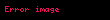

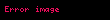
Xomski qrammatikasının çevirmələri baxılan sözdə qeyri-terminal simvol yoxa çıxana qədər tətbiq edilir. Bu qrammatika deduktivdir.
Sıfır, yaxud çoxsaylı əvəzləmələr 

Doğuran qrammatikanın tətbiqi ilə formal dilin qurulmasına aid misallar
Misal1. Fərz edək, 






İ

Bu halda "a" sözünün yeganə qurulması üsulu: İ 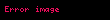
Misal2. 

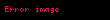

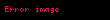
Qeyri-terminal 
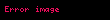
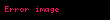


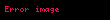

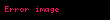

Misal3. Simmetrik sətirlər qrammatikasına baxaq, bunu G={V, W, I, P} ilə işarə edək. Burada: 


Doğuran qrammatikaların N. Xomski tərəfindən qurulmuş çətinlik dərəcəsinə görə təsnifatı
"0-cı sinif" qrammatikalar — Bu zaman 

Bütün formal qrammatikalar bu sinfə aid edilir. Türinq maşını ilə tanınan bütün dillər bu qrammatikalarla qurula bilir, belə dillərə rekursiv sadalanan dillər deyilir.
Misal. Aşağıda verilmiş qaydalara əsasən 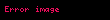
Qaydalar:

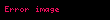
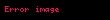
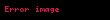

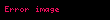
"1-ci sinif" qrammatikalar — Bu sinfə mətndən asılı qrammatikalar və qısaltmayan qrammatikalar aid edilir. Birincinin qaydaları aşağıdakı kimi verilir:


Qısaltmayan qrammatikanın qaydaları isə belədir:


Bu qrammatikalar ekvivalentdir. Bunlar təbii dilin mətnlərinin analizində istifadə oluna bilir. Bir sıra sahələrdə, məsələn, kompilyatorların qurulmasında istifadəsi, çətinliyə görə, praktiki olaraq mümkün deyil.
Bu sinifdən təbii dillərin və alt dillərin elementlərinin generasiyasında istifadə olunur.
"2-ci sinif" qrammatikalar — Bu qrammatikaların qaydaları 

"3-cü sinif" qrammatikalar(requlyar) — Bu qrammatikaların qaydaları 


Bu cür qrammatikaya avtomat, yaxud requlyar qrammatika deyilir. Bu qrammatikalar mətndən asılı deyil, məhdud imkanlara malikdir. Bunlar formal qrammatikalardan requlyar dilləri qura bilən ən sadə qrammatikalardır. Bu qrammatikaları iki ekvivalent sinfə ayırmaq olar:
- Sol tərəfli qrammatika
- Sağ tərəfli qrammatika
Sol tərəfli qrammatikanın operatorları:
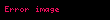

Sağ tərəfli qrammatikanın operatorları:
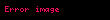

Sol tərəfli və sağ tərəfli qrammatikalar bir-birinə ekvivalentdir, bunlar eyni dil qurur. Ancaq onu da qeyd edək ki, sol tərəfli və sağ tərəfli qrammatikaların operatorlarını birləşdirsək, alınan dil requlyar olmaya bilər. Bundan başqa sağ tərəfli qrammatika ilə qurulan dillər çoxluğu sonlu avtomatlarla qurulan dillər çoxluğu ilə eynidir.
Əgər hər hansı 


Fərqli qrammatikaların bir-birinə çevrilməsi maraqlı məsələdir. Məsələn, doğuran qrammatika əsasında sadalayan qrammatika qurmaq olarmı? Olar. Bunun üçün doğuran qrammatika ilə sözləri generasiya etmək, onları uzunluğuna və simvollarının düzülüşünə görə nizamlamaq kifayətdir. Ancaq bunun əksinə, ümumi halda, hökm etmək olmaz, yəni hər bir sadalayan qrammatika əsasında doğuran qrammatika qurmaq olmaz. Sadalayan qrammatikadan tanıyan qrammatikanın qurulması da, ümumi halda, mümkün olmayan məsələdir. Ancaq birincinin əsasında ikincinin işini aşağıdakı kimi şərh etmık olar:
Sadalayan qrammatikanın çıxış sözlərini ardıcıl olaraq tanıyan qrammatikaya təqdim edək. Tanıyan qrammatikaya lazım olan söz çap olunduqda tanıyan qrammatika "hə" cavabı verir və biz sadalayan qrammatikanın işini məcburən dayandırırıq. Ancaq sadalayan qrammatikanın çıxışındakı heç bir söz verilmiş dilə aid olmasa, tanıma prosesi sonsuz olaraq davam edəcək, tanıyan qrammatikanın işi düyünə düşəcək. Bu mənada tanıyan qrammatikaların gücü doğuran və sadalayan qrammatikaların gücündən kiçikdir. Xomskinin doğuran qrammatikası ilə Türinqin tanıyan maşınlarını müqayisə etdikdə bu məsələni nəzərə almaq lazımdır.
Daha əlverişli qrammatika induktiv olan qrammatikadır.
Teorem 1: Hər bir təbii dilin sonlu sayda cümlələrindən ibarət çoxluq formal qrammatikadır.
Teorem 2: Hər bir formal dilə uyğun bir induktiv qrammatika qurmaq mümkündür.
Mətndən asılı olmayan ilk qrammatika kimi C. Bekusun yaratdığı ALQOL-60 dilini qeyd etmək olar.
Tezaurus formal qrammatikanın tətbiqinə aid bir nümunə kimi göstərilə bilər. Tezaurus cədvəl şəklində verilən modeldir(cədvələ baxın). Bu model baza sözlərinin əsasında cümlə qurmağa imkan verir.
| Sıra | Mətn | Qrammatik formasiya | Məna əlaqəsi |
|---|---|---|---|
| 1 | məlumat | *6,7 | 2>3 |
| 2 | istehlak | *4,3 | |
| 3 | müəssisə | *5 | 3>1 |
| 4 | at | ||
| 5 | si | ||
| 6 | in | *7 | |
| 7 | keyfiyyət | *8 | |
| 8 | i |
Bu tezaurusun "*" işarəsi mətndə verilən sözə yeni söz əlavə etmək imkanı yaradır. Belə ki, cümləni "məmulat" sözü ilə başlasaq, "məmulatın keyfiyyəti" cümləsi alınar.
Tezaurusdan kompüterdə informasiya bazası yaradan zaman verilənlər bazasının idarə edilməsi zamanı və s. müxtəlif sahələrdə istifadə olunur.
Formal qrammatikalardan biri də Bekus-Naur qrammatikasıdır. Bunun vasitəsilə "identifikator" anlayışının izahı aşağıdakı kimi verilir:
<identifikator> :: = <hərf> | <hərf> <davam>
<davam> :: = <simvol> | <simvol> <davam>
<simvol> :: = <hərf> | <rəqəm>
<hərf> :: = A | B | … | Z
<rəqəm> :: = 0| 1| 2| …| 9
Bekus-Naur qrammatikası əsasında başqa konstruksiyaları da yaratmaq olar, məsələn:
<isim> :: = <kök><şəkilçi>
<şəkilçi> :: = <tək halın şəkilçisi> | <cəm halın şəkilçisi>
Şərti işarələrin açıqlaması:
<… > —izahı tələb olunan hər hansı anlayış soldan və sağdan müvafiq olaraq bu işarələrlə əhatə olunur

| —bu işarə "və ya" mənasını bildirir
Göründüyü kimi, Bekus-Naur qrammatikasında hər hansı anlayış özünə istinad etməklə izah oluna bilir, yəni bu qrammatikada rekursivlikdən istifadə olunur.
Həmçinin bax
İstinadlar
- Vaqif Əsəd oğlu Kərimov. Alqoritmlər nəzəriyyəsi. Dərs vəsaiti. Bakı. ADNSU-nun nəşri, 2017.
Mənbə
- Vaqif Əsəd oğlu Kərimov. Alqoritmlər nəzəriyyəsi. Dərs vəsaiti. Bakı. ADNSU-nun nəşri, 2017, 116 səh.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Bu meqaleni vikilesdirmek lazimdir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Formal qrammatika dedikde ele qaydalar sistemi basa dusulur ki onun vasitesile verilmis formal dilin yalniz bu dilin duzgun sozleri qura bilir Qrammatika vasitesile qurulan formal dilin sozler coxlugu sonlu sonsuz ve ya bos coxluq ola biler Qrammatika sozler coxlugunu ixtiyari qaydada qura yaxud mueyyenlesdire biler Belelikle qrammatika sozlerin daxili qurulusunun qanunlarini aciqlayir ki bunlara sintaksis deyilir Formal qrammatika mueyyen sintaksis nezeriyye cercivesinde qurulan qrammatik riyazi modeldir Formal qrammatikanin novleriAlqoritmik noqteyi nezerden formal qrammatikalarin asagidaki novleri var Taniyan qrammatikalar Bu qrammatikalar bir nov ele qurgudur ki bunun girisine daxil olan soz verilmis dile aiddirse he aid deyilse yox cap olunur Sadalayan qrammatikalar Bu qrammatikalar verilmis dilin butun sozlerini bir bir cap etmekle sadalamaqla is gorur Aydindir ki dilin sozlerinin sayi sonsuz olarsa qrammatika hec zaman dayanmayacaq Ancaq qrammatikani mecburi o zaman dayandirmaq olar ki lazim olan soz cap olunmusdur Doguran qrammatikalar Bunlar ele qurgu dur ki dilin lazimli sozlerini qurur Doguran qrammatikalarin muxtelif variantlarini ABS riyaziyyatcisi ve linqivisti kecen esrin 50 ci illerinden etibaren yaratmaga baslamisdir Bir zamanlar hetta bu qrammatikalar tebii dillerin qurulmasi ucun istifade oluna bilen kimi ferz olunurdu lakin zaman bunlarin tebii diller sahesinde tetbiqi imkanlarini subut etmedi Hazirda doguran qrammatikalar esasen formal dillerin proqramlasdirma dillerinin sintaksisinin qurulmasinda muveffeqiyyetle istifade olunur Doguran qrammatika Terif Formal doguran qrammatika dedikde 4 obyektden ibaret bir formal G V W I P sistemi basa dusulur ki burada V a1 a2 am terminal simvollar elifbasi V A1 A2 An qeyri terminal simvollar elifbasidir Bunlarin kesismediyi ferz olunur V W displaystyle V cap W emptyset I displaystyle I aksiom yaxud baslangic qeyri terminal isare adlanir I W displaystyle I in W P displaystyle P cevirme yaxud qurulma qaydalarinin sonlu coxlugudur meselen a b displaystyle alpha beta yaxud a b displaystyle alpha to beta yazilisi onu gosterir ki a displaystyle alpha dan b displaystyle beta alinir burada a displaystyle alpha b displaystyle beta terminal ve qeyri terminal isarelerin birlesmesinden ibaret elifbadan qurulmus setirlerdir P a b b V W a V W displaystyle P alpha to beta mid beta in V cup W alpha in V cup W yeni a displaystyle alpha setrinin bos olmamasi serti ireli surulur a e displaystyle alpha neq e V displaystyle V elifbasi qrammatikanin aid oldugu dilin elifbasi ile eynidir Qrammatikanin qaydalarina gore a b displaystyle alpha beta cevrilmesinde vergulden sol terefde olan sozler yalniz terminal simvollardan ibaret olduqda qrammatika fealiyyetini dayandirir terminate Meqsede catana qeder qeyri terminal simvollar araliq sozleri qurmaq ucun istifade olunur Qeyri terminallarin teyinati curbecur ola biler ve qrammatikanin tipinden asilidir Ancaq yegane qeyri terminal simvol movcuddur ki qrammatikanin tipinden asili olmayaraq hemise eyni teyinata malikdir O dilin butun sozlerini isare etmek ucun istifade olunur Bu simvol doguran qrammatikanin baslangic qeyri terminal simvolu adlanir I ile isare olunur Her bir doguran qrammatikanin ele bir qayda olmalidir ki cevirmede vergulun sol terefini yalniz I olsun Bele olmasa bu qrammatika hec bir soz qura bilmez Xomski qrammatikasinin cevirmeleri baxilan sozde qeyri terminal simvol yoxa cixana qeder tetbiq edilir Bu qrammatika deduktivdir Sifir yaxud coxsayli evezlemeler displaystyle to seklinde tesvir oluna biler alpha beta displaystyle alpha to beta seklinde evezleme onu gosterir ki beta sozu alpha sozunden sonlu sayda evezleme ile alinmisdir Bu halda eger evezleme hec bir defe de tetbiq olunmamissa onda alpha ve beta sozleri ust uste dusur Doguran qrammatikanin tetbiqi ile formal dilin qurulmasina aid misallar Misal1 Ferz edek L displaystyle L dili yegane a displaystyle a simvolundan teskil olunmus yegane a displaystyle a sozunden ibaretdir L a displaystyle L a Bu sozu qurmaq ucun yegane I a displaystyle to a qaydasi kifayet eder Onu da qeyd edek ki a displaystyle a nin qurulmasini daha murekkeb yolla reallasdirmaq olar bunun ucun elave qeyri terminal simvoldan bunu A displaystyle A ile isare edek istifade edilmelidir Qurma qaydalarini daxil edek I A displaystyle to A A a displaystyle A to a Bu halda a sozunun yegane qurulmasi usulu I A a displaystyle to A to a seklinde tesvir oluna biler Qeyri terminal qrammatikanin elifbasini ixtiyari qaydada secmek mumkun oldugu ucun bele qenaete gele bilerik ki bu dili qurmaq ucun sonsuz sayda doguran qrammatika teklif oluna biler Misal2 L a a a a a a a a a displaystyle L a a a a a a a a a dilinin qurulmasi ucun doguran qrammatikani hazirlayaq Gorunduyu kimi dilin her bir sozu a displaystyle a simvolu ile baslayir ve bunun davaminda bir ve daha artiq a displaystyle a fraqmenti istirak edir Demeli evvelce a displaystyle a simvolunu qurmaq lazimdir bundan sonra buna lazim olan qeder a displaystyle a fraqmentini elave etmek lazimdir Qeyri terminal A displaystyle A simvolunu daxil edek Qrammatikanin qaydalarini operatorlarini daxil edek I aA displaystyle to aA A aA displaystyle A to aA A a displaystyle A to a a a a displaystyle a a a sozunun qurulmasi sxemi bele olar I aA a aA a a a displaystyle to aA to a aA to a a a Bu qurmada yuxaridaki operatorlardan her biri bir defe ardicil olaraq tetbiq olunmusdur L displaystyle L dilinin sozlerinin sayi sonsuz oldugu ucun butun sozleri rekursiv olaraq qurmaq teleb olunur Rekursiya yaradan sebeb A aA displaystyle A to aA operatorudur cevirmenin solunda ve saginda eyni bir simvol A displaystyle A simvolu istirak edir Misal3 Simmetrik setirler qrammatikasina baxaq bunu G V W I P ile isare edek Burada V a b displaystyle V a b W I displaystyle W I P I aIa I bIb I e displaystyle P I to aIa I to bIb I to e Bunlar esasinda gostermek olar ki G displaystyle G simmetrik qrammatikadir Doguran qrammatikalarin N Xomski terefinden qurulmus cetinlik derecesine gore tesnifati 0 ci sinif qrammatikalar Bu zaman alpha beta displaystyle alpha to beta cevirmesine hec bir mehdudiyyet qoyulmur ona gore de bunlara bezen qeyri mehdud qrammatika deyilir P a V W b V W displaystyle P alpha in V cap W beta in V cap W Butun formal qrammatikalar bu sinfe aid edilir Turinq masini ile taninan butun diller bu qrammatikalarla qurula bilir bele dillere rekursiv sadalanan diller deyilir Misal Asagida verilmis qaydalara esasen addd displaystyle addd sozunu qurmali Qaydalar I aBcc displaystyle I to aBcc B A displaystyle B to A BAA d displaystyle BAA to d Ac B displaystyle Ac to B A AAA dB displaystyle A to AAA mid dB I aBcc aAcc aBc aAc aB aA adB adAAA addBAA addd displaystyle I to aBcc to aAcc to aBc to aAc to aB to aA to adB to adAAA to addBAA to addd 1 ci sinif qrammatikalar Bu sinfe metnden asili qrammatikalar ve qisaltmayan qrammatikalar aid edilir Birincinin qaydalari asagidaki kimi verilir aAb awb displaystyle alpha A beta to alpha omega beta burada a b V W A W w V W displaystyle alpha beta in V cup W A in W omega in V cup W Qisaltmayan qrammatikanin qaydalari ise beledir a b displaystyle alpha to beta burada a b V W 1 a b displaystyle alpha beta in V cup W 1 leq mid alpha mid leq mid beta mid Bu qrammatikalar ekvivalentdir Bunlar tebii dilin metnlerinin analizinde istifade oluna bilir Bir sira sahelerde meselen kompilyatorlarin qurulmasinda istifadesi cetinliye gore praktiki olaraq mumkun deyil Bu sinifden tebii dillerin ve alt dillerin elementlerinin generasiyasinda istifade olunur 2 ci sinif qrammatikalar Bu qrammatikalarin qaydalari A a displaystyle A to alpha seklinde verilir A W a V W displaystyle A in W alpha in V cup W yeni bu qrammatika sol terefde yalniz bir qeyri terminal simvolun olmasini teleb edir Buna metnden asili olmayan qrammatika deyilir Bu qrammatikalar vasitesile qurulan diller maqazin yaddasli avtomatlar terefinden taninir 3 cu sinif qrammatikalar requlyar Bu qrammatikalarin qaydalari A aB A Ba displaystyle A to alpha B A to B alpha ve ya A a displaystyle A to alpha seklinde verilir burada A B W a V displaystyle A B in W alpha in V Bu cur qrammatikaya avtomat yaxud requlyar qrammatika deyilir Bu qrammatikalar metnden asili deyil mehdud imkanlara malikdir Bunlar formal qrammatikalardan requlyar dilleri qura bilen en sade qrammatikalardir Bu qrammatikalari iki ekvivalent sinfe ayirmaq olar Sol terefli qrammatika Sag terefli qrammatika Sol terefli qrammatikanin operatorlari A Ba displaystyle A to B alpha A a displaystyle A to alpha Sag terefli qrammatikanin operatorlari A aB displaystyle A to alpha B A a displaystyle A to alpha Sol terefli ve sag terefli qrammatikalar bir birine ekvivalentdir bunlar eyni dil qurur Ancaq onu da qeyd edek ki sol terefli ve sag terefli qrammatikalarin operatorlarini birlesdirsek alinan dil requlyar olmaya biler Bundan basqa sag terefli qrammatika ile qurulan diller coxlugu sonlu avtomatlarla qurulan diller coxlugu ile eynidir Eger her hansi L displaystyle L dil i displaystyle i ci sinif qrammatika ile qurulmussa onda deyirler ki bu dil i displaystyle i sinfine aiddir i displaystyle i sinfine aid olan butun qrammatikalar Gi displaystyle G i ile isare etsek onda formal qrammatikalar arasindaki elaqeni asagidaki kimi tesvir etmek olar Izahi N Xomskiye gore doguran qrammatikalarin hendesi interpretasiyasi Ferqli qrammatikalarin bir birine cevrilmesi maraqli meseledir Meselen doguran qrammatika esasinda sadalayan qrammatika qurmaq olarmi Olar Bunun ucun doguran qrammatika ile sozleri generasiya etmek onlari uzunluguna ve simvollarinin duzulusune gore nizamlamaq kifayetdir Ancaq bunun eksine umumi halda hokm etmek olmaz yeni her bir sadalayan qrammatika esasinda doguran qrammatika qurmaq olmaz Sadalayan qrammatikadan taniyan qrammatikanin qurulmasi da umumi halda mumkun olmayan meseledir Ancaq birincinin esasinda ikincinin isini asagidaki kimi serh etmik olar Sadalayan qrammatikanin cixis sozlerini ardicil olaraq taniyan qrammatikaya teqdim edek Taniyan qrammatikaya lazim olan soz cap olunduqda taniyan qrammatika he cavabi verir ve biz sadalayan qrammatikanin isini mecburen dayandiririq Ancaq sadalayan qrammatikanin cixisindaki hec bir soz verilmis dile aid olmasa tanima prosesi sonsuz olaraq davam edecek taniyan qrammatikanin isi duyune dusecek Bu menada taniyan qrammatikalarin gucu doguran ve sadalayan qrammatikalarin gucunden kicikdir Xomskinin doguran qrammatikasi ile Turinqin taniyan masinlarini muqayise etdikde bu meseleni nezere almaq lazimdir Daha elverisli qrammatika induktiv olan qrammatikadir Teorem 1 Her bir tebii dilin sonlu sayda cumlelerinden ibaret coxluq formal qrammatikadir Teorem 2 Her bir formal dile uygun bir induktiv qrammatika qurmaq mumkundur Metnden asili olmayan ilk qrammatika kimi C Bekusun yaratdigi ALQOL 60 dilini qeyd etmek olar Tezaurus formal qrammatikanin tetbiqine aid bir numune kimi gosterile biler Tezaurus cedvel seklinde verilen modeldir cedvele baxin Bu model baza sozlerinin esasinda cumle qurmaga imkan verir Tezaurusun qurulmasina aid numune Sira Metn Qrammatik formasiya Mena elaqesi1 melumat 6 7 2 gt 32 istehlak 4 33 muessise 5 3 gt 14 at5 si6 in 77 keyfiyyet 88 i Bu tezaurusun isaresi metnde verilen soze yeni soz elave etmek imkani yaradir Bele ki cumleni memulat sozu ile baslasaq memulatin keyfiyyeti cumlesi alinar Tezaurusdan komputerde informasiya bazasi yaradan zaman verilenler bazasinin idare edilmesi zamani ve s muxtelif sahelerde istifade olunur Formal qrammatikalardan biri de Bekus Naur qrammatikasidir Bunun vasitesile identifikator anlayisinin izahi asagidaki kimi verilir lt identifikator gt lt herf gt lt herf gt lt davam gt lt davam gt lt simvol gt lt simvol gt lt davam gt lt simvol gt lt herf gt lt reqem gt lt herf gt A B Z lt reqem gt 0 1 2 9 Bekus Naur qrammatikasi esasinda basqa konstruksiyalari da yaratmaq olar meselen lt isim gt lt kok gt lt sekilci gt lt sekilci gt lt tek halin sekilcisi gt lt cem halin sekilcisi gt Serti isarelerin aciqlamasi lt gt izahi teleb olunan her hansi anlayis soldan ve sagdan muvafiq olaraq bu isarelerle ehate olunur displaystyle bu isareden solda izah olunan anlayis sagda onun izahi yazilir bu isare ve ya menasini bildirir Gorunduyu kimi Bekus Naur qrammatikasinda her hansi anlayis ozune istinad etmekle izah oluna bilir yeni bu qrammatikada rekursivlikden istifade olunur Hemcinin baxAlqoritmlerIstinadlarVaqif Esed oglu Kerimov Alqoritmler nezeriyyesi Ders vesaiti Baki ADNSU nun nesri 2017 MenbeVaqif Esed oglu Kerimov Alqoritmler nezeriyyesi Ders vesaiti Baki ADNSU nun nesri 2017 116 seh
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans