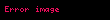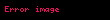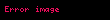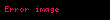De Morqan qanunları — Şotland riyaziyyatçısı Avqust de Morqan (1806-1871) adı ilə adlandırılıb. Avqust de Morqan ilk dəfə bu xassəni dəqiq ifadə etmiş və tam araşdırmışdır.
Təkliflər hesabının (nəzəriyyəsinin) xassəsi. Bu xassə təkliflərin konyuksiyasının (dizyunksiyasının) inkarının onların inkarının dizyunksiyası (konyuksiyası) ilə eyniqiymətli olduğunu müəyyənləşdirir. Başqa sözlə
De-Morqan qanunları istənilən Bul cəbrində, xüsusi halda, çoxluqlar cəbrində doğrudur. İxtiyari çoxluqları üçün
Burada , - tamamlama əməlidir.
Ədəbiyyat
- M.Mərdanov, S.Mirzəyev, Ş. Sadıqov Məktəblinin riyaziyyatdan izahlı lüğəti. Bakı 2016, "Radius nəşriyyatı", 296 səh.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
De Morqan qanunlari Sotland riyaziyyatcisi Avqust de Morqan 1806 1871 adi ile adlandirilib Avqust de Morqan ilk defe bu xasseni deqiq ifade etmis ve tam arasdirmisdir Teklifler hesabinin nezeriyyesinin xassesi Bu xasse tekliflerin konyuksiyasinin dizyunksiyasinin inkarinin onlarin inkarinin dizyunksiyasi konyuksiyasi ile eyniqiymetli oldugunu mueyyenlesdirir Basqa sozle A B A B displaystyle overline A land B overline A lor overline B ve A B A B displaystyle overline A lor B overline A land overline B De Morqan qanunlari istenilen Bul cebrinde xususi halda coxluqlar cebrinde dogrudur Ixtiyari A U B U displaystyle A subset U B subset U coxluqlari ucun A B A B A B A B displaystyle A cap B prime A prime cup B prime A cup B prime A prime cap B prime Burada X U X displaystyle X prime U backslash X X U displaystyle X subset U tamamlama emelidir EdebiyyatM Merdanov S Mirzeyev S Sadiqov Mekteblinin riyaziyyatdan izahli lugeti Baki 2016 Radius nesriyyati 296 seh
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans