Azərbaycanca AzərbaycancaБеларускі БеларускіDansk DanskDeutsch DeutschEspañola EspañolaFrançais FrançaisIndonesia IndonesiaItaliana Italiana日本語 日本語Қазақ ҚазақLietuvos LietuvosNederlands NederlandsPortuguês PortuguêsРусский Русскийසිංහල සිංහලแบบไทย แบบไทยTürkçe TürkçeУкраїнська Українська中國人 中國人United State United StateAfrikaans Afrikaans
Dəstək
www.wikimedia.az-az.nina.az

Düzbucaqlı üçbucaq bucaqlarından biri düz bucaq 90 olan üçbucağa deyilir Düzbucaqlı üçbucaq Düzbucaqlı üçbucaqda düz buc

Düzbucaqlı üçbucaq

Düzbucaqlı üçbucaq

Düzbucaqlı üçbucaq—bucaqlarından biri düz bucaq (90⁰) olan üçbucağa deyilir.

image
Düzbucaqlı üçbucaq

Düzbucaqlı üçbucaqda düz bucaq qarşısındakı tərəf hipotenuz, ona bitişik tərəflər, yəni iti bucaqlar qarşısında duran tərəflər isə katetlər adlanır.

Pifaqor teoreminə görə düzbucaqlı üçbucaqda katetlərin kvadratları cəmi hipotenuzun kvadratına bərabərdir. a²+b²=c²

Katetləri bərabər olan düzbucaqlı üçbucaq bərabəryanlı düzbucaqlı üçbucaq adlanır.

Xüsusiyyətləri

  • Düzbucaqlı üçbucağın iti bucaqlarının cəmi 90°-yə bərabərdir.
  • Düzbucaqlı üçbucağın xaricinə çəkilmiş çevrənin mərkəzi hipotenuzun orta nöqtəsidir.
  • Bərabəryanlı düzbucaqlı üçbucağın iti bucaqlarının hər biri 45°-yə bərabərdir.
  • Bərabəryanlı düzbucaqlı üçbucaqda hipotenuz katetin kök altında iki mislinə bərabərdir.
  • Düzbucaqlı üçbucaqda 30 dərəcəli bucaq qarşısında duran katet hipotenuzun yarısına bərabərdir.
  • Düzbucaqlı üçbucağın xaricinə çəkilmiş çevrənin radiusu hipotenuzun yarısına bərabərdir. R=c/2
  • Düzbucaqlı üçbucağın daxilinə çəkilmiş çevrənin radiusu r=(a+b-c)/2 düsturu ilə hesablanır (burada r-düzbucaqlı üçbucağın daxilinə çəkilmiş çevrənin radiusu, a və b katetlər, c-hipotenuzdur).
  • İti bucaqları 30°-60° olan düzbucaqlı üçbucaqda 60°-li bucaq qarşısındakı katet digər katetden kök altında 3 dəfə böyükdür.
  • Düz bucaqdan hipotenuza çəkilmiş hündürlüyün kvadratı onun hipotenuz üzərində böldüyü parçaların hasilinə bərabərdir.

Sahəsi

  1. Düzbucaqlı üçbucağın sahəsi katetlərinin hasilinin yarısına bərabərdir: S=a*b/2
  2. Heron düsturuna görə düzbucaqlı üçbucağın sahəsi kök altında onun yarımperimetri ilə hər bir katetin ayrı-ayrılıqda fərqinin hasilinə bərabərdir.
  3. Düzbucaqlı üçbucağın sahəsi onun daxilinə çəkilmiş çevrənin radiusu ilə bu radiusun hipotenuz ilə cəminin hasilinə bərabərdir.
  4. Düzbucaqlı üçbucağın sahəsi onun daxilinə çəkilmiş çevrənin hipotenuza toxunma nöqtəsində onu böldüyü hissələrin uzunluqları hasilinə bərabərdir.
  5. Bərabəryanlı düzbucaqlı üçbucağın sahəsi kvadratın sahəsinin yarısına bərabərdir. S=a²/2

Triqonometrik nisbətlər

  • Düzbucaqlı üçbucaqda iti bucağın sinusu bu bucağın qarşısındakı katetin hipotenuza nisbətinə deyilir.
  • Düzbucaqlı üçbucaqda iti bucağın kosinusu bu bucağa bitişik katetin hipotenuza nisbətinə deyilir.
  • Düzbucaqlı üçbucaqda iti bucağın tangensi bu bucağın qarşısındakı katetin bucağa bitişik katetə nisbətinə deyilir. Buradan alırıq ki:

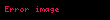
image

  • Düzbucaqlı üçbucaqda iti bucağın kotangensi bu bucağa bitişik katetin bucağın qarşısındakı katetə nisbətinə deyilir. Buradan alırıq ki:

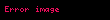
image

  • "Special Right Triangles" (ingilis). calculator.net. İstifadə tarixi: }7 may 2021.
  • "Düzbucaqlı üçbucağın sahəsi" (az.). jsoft.ws. 2021-05-17 tarixində . İstifadə tarixi: 2021-04-21.
  • "Right Triangle Trigonometry" (eng). math.libretexts.org. Jan 17, 2020. 2023-07-07 tarixində . İstifadə tarixi: 2021-02-04.

wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer

Duzbucaqli ucbucaq bucaqlarindan biri duz bucaq 90 olan ucbucaga deyilir Duzbucaqli ucbucaq Duzbucaqli ucbucaqda duz bucaq qarsisindaki teref hipotenuz ona bitisik terefler yeni iti bucaqlar qarsisinda duran terefler ise katetler adlanir Pifaqor teoremine gore duzbucaqli ucbucaqda katetlerin kvadratlari cemi hipotenuzun kvadratina beraberdir a b c Katetleri beraber olan duzbucaqli ucbucaq beraberyanli duzbucaqli ucbucaq adlanir XususiyyetleriDuzbucaqli ucbucagin iti bucaqlarinin cemi 90 ye beraberdir Duzbucaqli ucbucagin xaricine cekilmis cevrenin merkezi hipotenuzun orta noqtesidir Beraberyanli duzbucaqli ucbucagin iti bucaqlarinin her biri 45 ye beraberdir Beraberyanli duzbucaqli ucbucaqda hipotenuz katetin kok altinda iki misline beraberdir Duzbucaqli ucbucaqda 30 dereceli bucaq qarsisinda duran katet hipotenuzun yarisina beraberdir Duzbucaqli ucbucagin xaricine cekilmis cevrenin radiusu hipotenuzun yarisina beraberdir R c 2 Duzbucaqli ucbucagin daxiline cekilmis cevrenin radiusu r a b c 2 dusturu ile hesablanir burada r duzbucaqli ucbucagin daxiline cekilmis cevrenin radiusu a ve b katetler c hipotenuzdur Iti bucaqlari 30 60 olan duzbucaqli ucbucaqda 60 li bucaq qarsisindaki katet diger katetden kok altinda 3 defe boyukdur Duz bucaqdan hipotenuza cekilmis hundurluyun kvadrati onun hipotenuz uzerinde bolduyu parcalarin hasiline beraberdir SahesiDuzbucaqli ucbucagin sahesi katetlerinin hasilinin yarisina beraberdir S a b 2 Heron dusturuna gore duzbucaqli ucbucagin sahesi kok altinda onun yarimperimetri ile her bir katetin ayri ayriliqda ferqinin hasiline beraberdir Duzbucaqli ucbucagin sahesi onun daxiline cekilmis cevrenin radiusu ile bu radiusun hipotenuz ile ceminin hasiline beraberdir Duzbucaqli ucbucagin sahesi onun daxiline cekilmis cevrenin hipotenuza toxunma noqtesinde onu bolduyu hisselerin uzunluqlari hasiline beraberdir Beraberyanli duzbucaqli ucbucagin sahesi kvadratin sahesinin yarisina beraberdir S a 2Triqonometrik nisbetlerDuzbucaqli ucbucaqda iti bucagin sinusu bu bucagin qarsisindaki katetin hipotenuza nisbetine deyilir Duzbucaqli ucbucaqda iti bucagin kosinusu bu bucaga bitisik katetin hipotenuza nisbetine deyilir Duzbucaqli ucbucaqda iti bucagin tangensi bu bucagin qarsisindaki katetin bucaga bitisik katete nisbetine deyilir Buradan aliriq ki tga sinacosa displaystyle tg alpha frac sin alpha cos alpha Duzbucaqli ucbucaqda iti bucagin kotangensi bu bucaga bitisik katetin bucagin qarsisindaki katete nisbetine deyilir Buradan aliriq ki ctga cosasina displaystyle ctg alpha frac cos alpha sin alpha Special Right Triangles ingilis calculator net Istifade tarixi 7 may 2021 Duzbucaqli ucbucagin sahesi az jsoft ws 2021 05 17 tarixinde Istifade tarixi 2021 04 21 Right Triangle Trigonometry eng math libretexts org Jan 17 2020 2023 07 07 tarixinde Istifade tarixi 2021 02 04 ol Bu meqale qaralama halindadir Lutfen meqaleni umumvikipediya ve redakte qaydalarina uygun sekilde tertib edin Eger mumkundurse daha deqiq bir sablondan istifade edin section

Nəşr tarixi:
Yuxarı