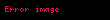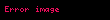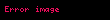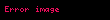Əgər ikitərtibli əyriyə nəzərən hər hansı istiqamət özünə olan istiqamətlə qoşma olarsa, baş istiqamət adlanır. Başqa sözlə öz qoşma istiqamətinə perependikulyar istiqamət baş istiqamətdir.
Qoşmalıq qarşılıqlı olduğundan baş istiqamət perependikulyar olan istiqamətin özü də baş istiqamətdir. sistemində baş istiqamət vekorudur. Onda və qoşma olmalıdır. Yəni,
1)
2) ödənməlidir. 1)-i nəzərə alsaq, buradan da
alınır. Bu tənlik baş istiqamətlərin müəyyən edilməsinə imkan yaradır.
Aşağıdakı hallara baxaq:
1. olarsa, işarə etsək
Buradan alınır ki, əyrisinə nəzərən yalnız iki baş istiqamət vardır.
2. , onda tənlik
olar. Bu halda da əyrisinə nəzərən yalnız 2 baş istiqamət var.
3. , onda vektorunun istiqaməti baş istiqamət olar. Bu halda əyri çevrə olar(həqiqi , xəyali və ya 0 radiuslu).
İsbat etdik ki, teorem doğrudur. Hər bir iki tərtibli əyriyə nəzərən yalnız iki baş istiqamət vardır. Çevrəyə nəzərən isə müstəvinin hər bir istiqaməti baş istiqamət olar.
Tərif: Baş istiqamət qoşma olan diametri baş diametri adlanır və ya diametr özü ilə qoşma olan istiqamətə olarsa baş diametri adlanır.
Xarici keçidlər
Analitik həndəsə aid kitablar
Xanəli Paşayev, Maqsud Nəcəfov Analitik həndəsədən mühazirələr, Dərs vəsaiti, “Çaşıoğlu” nəşriyyatı, 2013,200 səh. 2017-01-17 at the Wayback Machine
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Eger ikitertibli eyriye nezeren her hansi istiqamet ozune olan istiqametle qosma olarsa bas istiqamet adlanir Basqa sozle oz qosma istiqametine perependikulyar istiqamet bas istiqametdir Qosmaliq qarsiliqli oldugundan bas istiqamet perependikulyar olan istiqametin ozu de bas istiqametdir 0 i j displaystyle 0 i j sisteminde p p1 p2 displaystyle vec p p 1 p 2 bas istiqamet vekorudur Onda p q displaystyle vec p bot vec q ve p displaystyle vec p qosma q displaystyle vec q olmalidir Yeni 1 p1q1 p2q2 0 displaystyle p 1 q 1 p 2 q 2 0 2 a11p1q1 a12 p1q2 p2q1 a22p2q2 0 displaystyle a 11 p 1 q 1 a 12 p 1 q 2 p 2 q 1 a 22 p 2 q 2 0 odenmelidir 1 i nezere alsaq a11p1q1 a12 p1q1 p2q2 a22p2q2 0 displaystyle a 11 p 1 q 1 a 12 p 1 q 1 p 2 q 2 a 22 p 2 q 2 0 buradan da a11 p12 p22 a22 a11 p2p1 0 displaystyle a 11 p 1 2 p 2 2 a 22 a 11 p 2 p 1 0 alinir Bu tenlik bas istiqametlerin mueyyen edilmesine imkan yaradir Asagidaki hallara baxaq 1 a12 0 p1 0 displaystyle a 12 neq 0 p 1 neq 0 olarsa p 0 k p2p1 displaystyle vec p neq 0 k frac p 2 p 1 isare etsek k2a12 a11a22 k a12 0 k1 2 a22a11 a11a22 2 4a1222a12 k1 k2 1 displaystyle k 2 a 12 a 11 a 22 k a 12 0 k 1 2 frac a 22 a 11 pm sqrt a 11 a 22 2 4a 12 2 2a 12 k 1 cdot k 2 1 Buradan alinir ki g displaystyle gamma eyrisine nezeren yalniz iki bas istiqamet vardir 2 a12 0 a22 a11 0 displaystyle a 12 0 a 22 a 11 neq 0 onda tenlik a22 a11 p2p1 p1 p2 0 p1 0 p2 0 p1 0 p2 0 displaystyle a 22 a 11 p 2 p 1 p 1 cdot p 2 0 p 1 0 p 2 0 p 1 neq 0 p 2 neq 0 olar Bu halda da g displaystyle gamma eyrisine nezeren yalniz 2 bas istiqamet var 3 a12 0 a22 a11 0 displaystyle a 12 0 a 22 a 11 0 onda p p1 p2 0 displaystyle forall vec p p 1 p 2 neq vec 0 vektorunun istiqameti bas istiqamet olar Bu halda eyri cevre olar heqiqi xeyali ve ya 0 radiuslu Isbat etdik ki teorem dogrudur Her bir iki tertibli eyriye nezeren yalniz iki bas istiqamet vardir Cevreye nezeren ise mustevinin her bir istiqameti bas istiqamet olar Terif Bas istiqamet qosma olan diametri bas diametri adlanir ve ya diametr ozu ile qosma olan istiqamete displaystyle bot olarsa bas diametri adlanir Xarici kecidlerAnalitik hendese aid kitablar Xaneli Pasayev Maqsud Necefov Analitik hendeseden muhazireler Ders vesaiti Casioglu nesriyyati 2013 200 seh 2017 01 17 at the Wayback Machine
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans