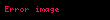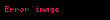Sərbəst dəyişən , axtarılan funksiya və onun törəməsi arasıda verilmiş
Tutaq ki, funksiyası müstəvisinin muəyyən bir oblastında təyin olunmuşdur.
Оblast dedikdə, aşağıdakı 2 şərtini ödəyən boş olmayan nöqtələr çoxluğu başa düşülür:
1) açıq çoxluqdur, yəni onun hər bir nöqtəsi özünün müəyyən bir ətrafı ilə bu çoxluğa daxildir;
2) çoxluğu əlaqəli çoxluqdur, yəni onun istənilən iki nöqtəsini tamamilə – nin daxilində yerləşən və təşkilediçilərinin sayı sonlu olan sınıq xətt vasitəsilə birləşdirmək olar.
Tərif. Əgər inteqralında diferensiallanan funksiyası
şərtlərini ödəyirsə, həmin funksiyaya (2) tənliyinin intervalında həlli deyilir.
Bəzən diferensial tənliyin həllinin qeyri – aşkar funksiya kimi və ya parametrik şəkildə tapmaq əlverişli olur.
Tərif. Əgər
bərabərliyindən qeyri – aşkar funksiya kimi təyin olunan funksiyası (2) tənliyinin həlli olarsa, (3) münasibətinə (2) tənliyinin qeyri – aşkar şəkildə həlli deyilir.
Tərif. Parametrik şəkildə verilmiş
1)
2) sonlu törəmələri və
3) bərabərliyi ödənirsə, onda (4) funksiyasına (2) tənliyinin inteqralında parametrik şəklində həlli deyilir.
Misallar: 1. tənliyi birtərtibli aidi diferensial tənlikdir. İnteqral hesabından bilirik ki, onun həlli düsturu ilə təyin olunur. Bu düsturdan görürük ki, tənliyi bir yox, sonsuz sayda həllə malikdir. Burada ixtiyari sabitdir.
Ümumiyyətlə, - tərtibli tənliyin həlli isə dənə sabitdən asılı olan
həllər ailəsinə malikdir.
2. funksiyası tənliyinin həllidir.
Doğrudan da, funksiyası inteqralında təyin olunmuş və diferensiallanandır, onu tənlikdə nəzərə alsaq
3. funksiyası tənliyinin aralığında həllidir.
Doğrudan da
Kütləsi olan maddi nöqtə müəyyən yüksəklikdən ağırlıq qüvvəsinin təsiri ilə sərbəst düşür. Havanın miqavimətini nəzərə almadan nöqtəyə təsir edən qüvvəsi onun hərəkətinin təcili vasitəsilə
Həmçinin bax
Ədəbiyyat
- 1.Q.Т.əhmədov, К.Q.Həsənov, М.H.Yaqubov, Adi diferensial tənliklər kursu, Bakı, Maarif, 1978.
- 2.И.Г.Петровский, Лекции по теории обыкновенных дифференциальных уравнений, М., Наука, 1984.
- 3.Л.С.Понтрягин, Обыкновеные дифференциальные уравнения, М., Наука, 1982.
- 4.В.В.Степанов, Курс дифференциальных уравнений, М.,1959.
- 5.А.Ф.Филиппов, Сборник задач по дифференциальным уравнениям, М., 2004. 2017-07-21 at the Wayback Machine
- 6.Х.М.Quliyev, К.Q.Həsənov, Diferensial tənliklər. Məsələ və misallar həlləri ilə, Bakı, Çaşıoğlu, 2001.
- 7.М.H.Yaqubov, Y.Т.Mehrəliyev, Birtərtibli adi diferensial tənliklər, BDU, Bakı, 1999.
- 8.Л.Э.Эльсгольц, Дифференциальные уравнения и вариационные исчисление, Москва, 1969.
- 9.Н.М.Матвеев, Методы интегрирования обыкновеных дифференциальных уравнений, Минск, Выщэйщая школа, 1974.
- 10.А.Н.Тихонов, А.Б.Васильева, А.Г.Свешников, Дифференциальные уравнения, Москва, Наука, 1985.
wikipedia, oxu, kitab, kitabxana, axtar, tap, meqaleler, kitablar, oyrenmek, wiki, bilgi, tarix, tarixi, endir, indir, yukle, izlə, izle, mobil, telefon ucun, azeri, azəri, azerbaycanca, azərbaycanca, sayt, yüklə, pulsuz, pulsuz yüklə, haqqında, haqqinda, məlumat, melumat, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, şəkil, muisiqi, mahnı, kino, film, kitab, oyun, oyunlar, android, ios, apple, samsung, iphone, pc, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, web, computer, komputer
Serbest deyisen x displaystyle x axtarilan funksiya y x displaystyle y left x right ve onun toremesi y x displaystyle y prime left x right arasida verilmisF x y y 0 1 displaystyle F left x y y prime right 0 1 munasibetine birtertibli adi diferensial tenlik deyilir Aydindir ki F x y z displaystyle F left x y z right funksiyasi x y displaystyle x y deyisenlerinin birinden ve ya her ikisinden asili olmaya da biler lakin 1 tenliyinin diferensial tenlik olmasi ucun bu funksiya z displaystyle z den hokmen asili olmalidir y f x y 2 displaystyle y prime f left x y right 2 seklinde olan tenliye toremeye nezeren hell olunmus birtertibli aid diferensial tenlik deyilir Tutaq ki f x y displaystyle f left x y right funksiyasi XOY displaystyle XOY mustevisinin mueyyen bir D displaystyle D oblastinda teyin olunmusdur Oblast dedikde asagidaki 2 sertini odeyen bos olmayan D displaystyle D noqteler coxlugu basa dusulur 1 D displaystyle D aciq coxluqdur yeni onun her bir noqtesi ozunun mueyyen bir etrafi ile bu coxluga daxildir 2 D displaystyle D coxlugu elaqeli coxluqdur yeni onun istenilen iki noqtesini tamamile D displaystyle D nin daxilinde yerlesen ve teskiledicilerinin sayi sonlu olan siniq xett vasitesile birlesdirmek olar Terif Eger a b displaystyle left a b right inteqralinda diferensiallanan y f x displaystyle y varphi left x right funksiyasi1 x f x D x a b 2 f x f x f x x a b displaystyle begin array l 1 left x varphi left x right right in D x in left a b right 2 varphi left x right f left x varphi left x right right x in left a b right end array sertlerini odeyirse hemin funksiyaya 2 tenliyinin a b displaystyle left a b right intervalinda helli deyilir Bezen diferensial tenliyin hellinin qeyri askar funksiya kimi ve ya parametrik sekilde tapmaq elverisli olur Terif Egerϕ x y 0 3 displaystyle phi left x y right 0 3 beraberliyinden qeyri askar funksiya kimi teyin olunan y f x displaystyle y varphi left x right funksiyasi 2 tenliyinin helli olarsa 3 munasibetine 2 tenliyinin qeyri askar sekilde helli deyilir Terif Parametrik sekilde verilmisx f x y ps t t a b 4 displaystyle x varphi left x right y psi left t right t in left alpha beta right 4 funksiyasi her bir t displaystyle t ucun 1 f t ps t D displaystyle left varphi left t right psi left t right right in D 2 x f t y ps t f t 0 displaystyle x prime varphi prime left t right y prime psi prime left t right left varphi prime left t right neq 0 right sonlu toremeleri ve 3 ps t f t f f t ps t displaystyle frac psi prime left t right varphi prime left t right f left varphi left t right psi left t right right beraberliyi odenirse onda 4 funksiyasina 2 tenliyinin a b displaystyle left alpha beta right inteqralinda parametrik seklinde helli deyilir Misallar 1 y 2x displaystyle y prime 2x tenliyi birtertibli aidi diferensial tenlikdir Inteqral hesabindan bilirik ki onun helli y x2 c lt x lt displaystyle y x 2 c left infty lt x lt infty right dusturu ile teyin olunur Bu dusturdan goruruk ki y 2x displaystyle y prime 2x tenliyi bir yox sonsuz sayda helle malikdir Burada C displaystyle C ixtiyari sabitdir Umumiyyetle y n 0 displaystyle y left n right 0 n displaystyle n tertibli tenliyin helli ise n displaystyle n dene sabitden asili olany c1xn 1 c2xn 2 cn 1x cn displaystyle y c 1 x n 1 c 2 x n 2 c n 1 x c n heller ailesine malikdir 2 y e2x ex displaystyle y e 2x e x funksiyasi y y e2x displaystyle y prime y e 2x tenliyinin hellidir Dogrudan da y e2x ex displaystyle y e 2x e x funksiyasi displaystyle left infty infty right inteqralinda teyin olunmus ve diferensiallanandir onu tenlikde nezere alsaq2e2x ex e2x ex e2x displaystyle 2e 2x e x e 2x e x e 2x x displaystyle x in butun qiymetlerinde dogru oldugunugorerik 3 x acos t y bsin t displaystyle x a cos t y b sin t funksiyasi y b2a2 xy displaystyle y prime frac b 2 a 2 cdot frac x y tenliyinin araliginda hellidir Dogrudan dabcos t asin t b2a2 acos tbsin t displaystyle frac b cos t a sin t frac b 2 a 2 cdot frac a cos t b sin t mexanika ve s kimi muxtelif elm sahelerinin ve texnikanin bir cox muhum meselelerinin helli diferensial tenliklere getirilir Bunu asagidaki misalda izah edek Kutlesi m displaystyle m olan maddi noqte mueyyen yukseklikden agirliq quvvesinin tesiri ile serbest dusur Havanin miqavimetini nezere almadan noqteye tesir eden F displaystyle F quvvesi onun hereketinin a displaystyle a tecili vasitesileF ma displaystyle F ma kimi tapilir Nyuton II qanunu Noqteye ancaq agirliq quvvesi tesir etdiyinden F p mg displaystyle F p mg olar a d2s t dt2 S t S t gS t gt22 c1t c2 displaystyle begin array l a frac d 2s left t right dt 2 S prime prime left t right S prime prime left t right g S left t right frac gt 2 2 c 1 t c 2 end array S 0 V0 displaystyle S prime left 0 right V 0 ve S 0 S0 displaystyle S left 0 right S 0 melum olarsa ve C1 V0 displaystyle C 1 V 0 ve C2 S0 displaystyle C 2 S 0 S t gt22 V0t S0 displaystyle S left t right frac gt 2 2 V 0 t S 0 Hemcinin baxRiyaziyyatTenlikEdebiyyat1 Q T ehmedov K Q Hesenov M H Yaqubov Adi diferensial tenlikler kursu Baki Maarif 1978 2 I G Petrovskij Lekcii po teorii obyknovennyh differencialnyh uravnenij M Nauka 1984 3 L S Pontryagin Obyknovenye differencialnye uravneniya M Nauka 1982 4 V V Stepanov Kurs differencialnyh uravnenij M 1959 5 A F Filippov Sbornik zadach po differencialnym uravneniyam M 2004 2017 07 21 at the Wayback Machine6 H M Quliyev K Q Hesenov Diferensial tenlikler Mesele ve misallar helleri ile Baki Casioglu 2001 7 M H Yaqubov Y T Mehreliyev Birtertibli adi diferensial tenlikler BDU Baki 1999 8 L E Elsgolc Differencialnye uravneniya i variacionnye ischislenie Moskva 1969 9 N M Matveev Metody integrirovaniya obyknovenyh differencialnyh uravnenij Minsk Vyshejshaya shkola 1974 10 A N Tihonov A B Vasileva A G Sveshnikov Differencialnye uravneniya Moskva Nauka 1985
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State